Hostname: page-component-77c89778f8-swr86 Total loading time: 0 Render date: 2024-07-16T15:06:39.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Prevalent Lq-dimensions of measures

Published online by Cambridge University Press:  24 June 2010

L. OLSEN
L. OLSEN*
Affiliation:
Department of Mathematics, University of St. Andrews, St. Andrews, Fife KY16 9SS, Scotland. e-mail: lo@st-and.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be a compact subset of ℝd and write s for the Hausdorff dimension of K. For a probability measure μ on K, the lower and upper Lq-dimensions of order q ∈ ℝ are defined by 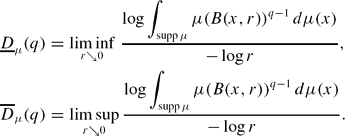In this paper we study Lq-dimensions of measures that are generic in the sense of prevalence. 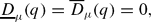In particular, we prove that if K satisfies a mild regularity condition, then a prevalent probability measure μ on K satisfies: for all 0 ≤ q ≤ 1, and for all 1 ≤ q. This result is in sharp contrast to the behaviour of the Lq-dimensions of measures that are generic in the sense of Baire category. Namely, if K satisfies a mild regularity condition, then a probability measure μ on K that is generic in the sense of Baire category satisfies: 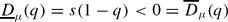for all 1 < q.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 149 , Issue 3 , November 2010 , pp. 553 - 571
Copyright
Copyright © Cambridge Philosophical Society 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AZ]Anderson, R. and Zame, W.Genericity with infinitely many parameters. Adv. Theor. Econ. 1 2001 Art. 1, 64 pp. (electronic).Google Scholar
[BN]Buczolich, Z. and Nagy, J.Hölder spectrum of typical monotone continuous functions. Real Anal. Exchange 26 2000/01 133–156.CrossRefGoogle Scholar
[Ch1]Christensen, J. P. R.On sets of Haar measure zero in abelian Polish group. Israel J. Math. 13 1972 255–260.CrossRefGoogle Scholar
[Ch2]Christensen, J. P. R.Topology and Borel structure (North-Holland, 1974).Google Scholar
[DS]David, G. and Semmes, S.Fractured fractals and broken dreams. Self-similar geometry through metric and measure. Oxford Lecture Series in Mathematics and its Applications, 7(The Clarendon Press, 1997).CrossRefGoogle Scholar
[Fa]Falconer, K. J.Techniques in Fractal Geometry (John Wiley & Sons, Ltd., 1997).Google Scholar
[FJ1]Fraysse, A. and Jaffard, S. The Sobolev embeddings are usually sharp. Abstr. Appl. Anal. 2005 437–448.CrossRefGoogle Scholar
[FJ2]Fraysse, A. and Jaffard, S.How smooth is almost every function in a Sobolev space? Rev. Mat. Iberoam. 22 2006 663–682.CrossRefGoogle Scholar
[FJK]Fraysse, A., Jaffard, S. and Kahane, J.-P.Quelques propriétés génériques en analyse. C. R. Math. Acad. Sci. Paris 340 2005 645–651.CrossRefGoogle Scholar
[Fr]Fraysse, A.Generic validity of the multifractal formalism. SIAM J. Math. Anal. 39 2007 593–60.CrossRefGoogle Scholar
[Ge]Genyuk, J.A typical measure typically has no local dimension. Real Anal. Exchange 23 1997/98 525–537.CrossRefGoogle Scholar
[Ha]Haase, H. A survey on the dimension of measures. Topology, measures, and fractals (Warnemünde, 1991), 66–75, Math. Res. 66(Akademie-Verlag, 1992).Google Scholar
[HK]Hunt, B. and Kaloshin, V.How projections affect the dimension spectrum of fractal measures. Nonlinearity 10 1997 1031–1046.CrossRefGoogle Scholar
[HSY]Hunt, B., Sauer, T. and Yorke, J.Prevalence: a translation-invariant “almost every” on infinite-dimensional spaces. Bull. Amer. Math. Soc. (N.S.) 27 (1992) 217–238.CrossRefGoogle Scholar
[Hun]Hunt, B.The prevalence of continuous nowhere differentiable functions. Proc. Amer. Math. Soc. 122 (1994) 711–717.CrossRefGoogle Scholar
[Hut]Hutchinson, J.Fractals and self-similarity. Indiana Univ. Math. J. 30 (1981) 713–747.CrossRefGoogle Scholar
[Ja1]Jaffard, S.On the Frisch-Parisi conjecture. J. Math. Pure Appl. 79 (2000) 525–552.CrossRefGoogle Scholar
[Ja2]Jaffard, S.Conjecture de Frisch et Parisi et généricité des fonctions multifractales. C. R. Acad. Sci. Paris Sér. I Math. 330 (2000) 265–270.CrossRefGoogle Scholar
[La]Lau, K.-S. Self-similarity, Lp-spectrum and multifractal formalism. Fractal geometry and stochastics (Finsterbergen, 1994), 55–90, Progr. Probab. 37, (Birkhuser, 1995).Google Scholar
[LN]Lau, K.-S. and Ngai, S.-M.Multifractal measures and a weak separation condition. Adv. Math. 141 (1999) 45–96.CrossRefGoogle Scholar
[Ol1]Olsen, L.Typical Lq-dimensions of measures. Monathsh. Math. 146 (2005) 143–157.CrossRefGoogle Scholar
[Ol2]Olsen, L.Typical upper Lq-dimensions of measures for q ∈ [0, 1]. Bull. Sci. Math. 132 (2008) 551–561.CrossRefGoogle Scholar
[OHK]Ott, W., Hunt, B. and Kaloshin, V.The effect of projections on fractal sets and measures in Banach spaces. Ergodic Theory Dynam. Systems 26 (2006) 869–891.CrossRefGoogle Scholar
[OY]Ott, W. and Yorke, J.Prevalence. Bull. Amer. Math. Soc. (N.S.) 42 (2005) 263–290.CrossRefGoogle Scholar
[Pa]Parthasarathy, K. R.Probability Measures on Metric Spaces (Academic Press, Inc., 1967).CrossRefGoogle Scholar
[o]Volkmann, B.Über extreme Anormalität bei Ziffernentwicklungen. Math. Ann. 190 (1970/1971) 149–153.CrossRefGoogle Scholar