Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-21T13:02:48.590Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive definite *-spherical functions, property (T) and C*-completions of Gelfand pairs

Published online by Cambridge University Press:  26 October 2015

NADIA S. LARSEN  and
RUI PALMA
NADIA S. LARSEN
Affiliation:
Department of Mathematics, University of Oslo, PO BOX 1053, Blindern, Norway. e-mail: nadiasl@math.uio.no
RUI PALMA
Affiliation:
e-mail: ruiiiipalma@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The study of existence of a universal C*-completion of the *-algebra canonically associated to a Hecke pair was initiated by Hall, who proved that the Hecke algebra associated to (SL2(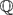$\mathbb{Q}$p), SL2(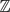$\mathbb{Z}$p)) does not admit a universal C*-completion. Kaliszewski, Landstad and Quigg studied the problem by placing it in the framework of Fell–Rieffel equivalence, and highlighted the role of other C*-completions. In the case of the pair (SLn(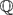$\mathbb{Q}$p), SLn(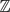$\mathbb{Z}$p)) for n ⩾ 3 we show, invoking property (T) of SLn(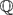$\mathbb{Q}$p), that the C*-completion of the L1-Banach algebra and the corner of C*(SLn(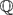$\mathbb{Q}$p)) determined by the subgroup are distinct. In fact, we prove a more general result valid for a simple algebraic group of rank at least 2 over a 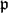$\mathfrak{p}$-adic field with a good choice of a maximal compact open subgroup.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 160 , Issue 1 , January 2016 , pp. 77 - 93
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Anantharaman-Delaroche, C. Approximation properties for coset spaces and their operator algebras. preprint, http://www.univ-orleans.fr/mapmo/membres/anantharaman/Almost_normal_v2.pdf.Google Scholar
[2]Bekka, B., de la Harpe, P. and Valette, A.Kazhdan's property (T). New Mathematical Monographs, 11 (Cambridge University Press, Cambridge, 2008).Google Scholar
[3]Bost, J.-B. and Connes, A.Hecke algebras, type III factors and phase transitions with spontaneous symmetry breaking in number theory. Selecta Math. (New Series) 1 (1995), 411–457.CrossRefGoogle Scholar
[4]Bourbaki, N.Elements of Mathematics, Lie Groups and Lie Algebras. Chapters 4-6 (Springer-Verlag, Berlin 2002).CrossRefGoogle Scholar
[5]Bratteli, O. and Robinson, D.Operator Algebras and Quantum Statistical Mechanics 1, 2nd edition (Springer–Verlag, New York, 1987).CrossRefGoogle Scholar
[6]Dieudonné, J.Gelfand pairs and spherical functions. Internat. J. Math. & Math. Sci. 2 no. 2 (1979), 153–162.CrossRefGoogle Scholar
[7]Dixmier, J.Les Algèbres D'opérateurs dans L'espace Hilbertiens. 2(eme) èdition, (Gauthier–Villars, Paris, 1969).Google Scholar
[8]Godement, R.A theory of spherical functions, I. Trans. Amer. Math. Soc. 73 (1952), 496–556.CrossRefGoogle Scholar
[9]Hall, R. W. Hecke C*-algebras. PhD. thesis. The Pennsylvania State University (1999).Google Scholar
[10]Kaliszewski, S., Landstad, M. B. and Quigg, J.Hecke C*-algebras, Schlichting completions and Morita equivalence. Proc. Edinb. Math. Soc. (2) 51 no. 3 (2008), 657–695.CrossRefGoogle Scholar
[11]Krieg, A.Hecke algebras. Mem. Amer. Math. Soc. 87 (1990), No. 435.Google Scholar
[12]Lang, S. SL2($\mathbb{R}$). (Addison–Wesley, 1975).Google Scholar
[13]Macdonald, I. G.Harmonic analysis on semi-simple groups, Actes, 2. Congrés Intern. Math. (1970), 331–335.Google Scholar
[14]Palma, R.Quasi-symmetric group algebras and C*-completions of Hecke algebras. Operator Algebra and Dynamics. Springer Proc. Math. Statistics, Vol. 58 (2013), 253–271.CrossRefGoogle Scholar
[15]Palmer, T. W.Banach algebras and the general theory of *-algebras. Vol. II *-Algebras. Encyc. of Math. Appl., vol. 79 (Cambridge University Press, Cambridge 2001).Google Scholar
[16]Raeburn, I. and Williams, D. P.Morita equivalence and continuous-trace C*-algebras. Math. Surveys Monogr., 60, Amer. Math. Soc. (Providence, RI, 1998).CrossRefGoogle Scholar
[17]Satake, I.On spherical functions over $\mathfrak{p}$-adic fields. Proc. Japan Acad. 38 (1962), 422–425.Google Scholar
[18]Satake, I.Theory of spherical functions on reductive algebraic groups over $\mathfrak{p}$-adic fields. Inst. Hautes Études Sci. Publ. Math. (1963), no. 18, 5–69.CrossRefGoogle Scholar
[19]Schlichting, G.Polynomidentitäten und Permutationsdarstellungen lokalkompakter Gruppen, Invent. Math. 55 (1979), 97–106.CrossRefGoogle Scholar
[20]Shirbisheh, V. Locally compact Hecke pairs and property (RD). Preprint, arXiv:1402.2529v2[math.GR].Google Scholar
[21]Tzanev, K.Hecke C*-algebras and amenability. J. Operator Theory 50 no. 1 (2003), 169–178.Google Scholar
[22]Tzanev, K.C*-algèbre de Hecke et K-theorie. thèse. Universite Paris VII (2000).Google Scholar
[23]Valette, A.A global approach to spherical functions on rank 1 symmetric spaces. Nieuw. Arch. Wisk. (4) 5 (1987) (1), 33–52.Google Scholar