Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-18T18:51:05.375Z Has data issue: false hasContentIssue false
  • English
  • Français

The perturbation of relatively open operators with reduced index

Published online by Cambridge University Press:  24 October 2008

L. E. Labuschagne
L. E. Labuschagne
Affiliation:
Department of Mathematics, University of Stellenbosch, 7600 Stellenbosch, South Africa
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X and Y denote normed spaces and T:D(T) ⊂ X → Y a linear transformation. It is shown that even in the case where both X and Y are incomplete, the quantity 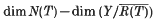remains constant under both small and compact perturbation, provided that T is relatively open, R(T) is closed, and the perturbation is made in the right ‘direction’. If in addition 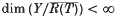and N(T) is topologically complemented, the topological complementation of the kernel is also preserved under small perturbations made in the right ‘direction’ and arbitrary compact perturbation. Various counter-examples are exhibited proving these results to be best possible.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 112 , Issue 2 , September 1992 , pp. 385 - 402
Copyright
Copyright © Cambridge Philosophical Society 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cross, R. W.. On the continuous linear image of a Banach space. J. Austral. Math. Soc. Ser. A 29 (1980), 219–234.CrossRefGoogle Scholar
[2]Cross, R. W.. Properties of some norm related functions of unbounded linear operators. Math. Z. 199 (1988), 285–302.CrossRefGoogle Scholar
[3]Cross, R. W.. Some continuity properties of linear transformations in normed spaces. Glasgow Math. J. 30 (1988), 243–247.CrossRefGoogle Scholar
[4]Cross, R. W.. Unbounded linear transformations of upper semi-Fredholm type in normed spaces. Portugal Math. (1) 47 (1990), 61–79.Google Scholar
[5]Cross, R. W.. On the perturbation of unbounded linear operators with topologically complemented ranges. J. Funct. Anal. (2) 92 (1990), 468–473.CrossRefGoogle Scholar
[6]Cross, R. W. and Labuschagne, L. E.. Characterisations of operators of lower semi-Fredholm type in normed linear spaces. Quaestiones Math., to appear.Google Scholar
[7]de Wilde, M. and Chu, Le Quang. Perturbation of maps in locally convex spaces. Math. Ann. 215 (1975), 215–233.CrossRefGoogle Scholar
[8]Dieudonné, J.. Sur les homomorphismes d'espaces normés. Bull. Sci. Math. 67 (1943), 72–84.Google Scholar
[9]Goldberg, S.. Unbounded Linear Operators (McGraw-Hill, 1966; Dover, 1985).Google Scholar
[10]Gol'dman, M. A. and Kračkovskii, S. N.. Perturbation of homomorphisms by operators of finite rank. Soviet Math. Dokl. 8 (1967), 670–673.Google Scholar
[11]Harte, R.. Invertibility and Singularity for Bounded Linear Operators (Marcel Dekker, 1988).Google Scholar
[12]Jarchow, H.. Locally Convex Spaces (B. G. Teubner, 1981).CrossRefGoogle Scholar
[13]Kato, T.. Perturbation theory for nullity, deficiency and other quantities of linear operators. J. Analyse Math. 6 (1958), 273–322.CrossRefGoogle Scholar
[14]Labuschagne, L. E.. Functions of operators and the classes associated with them. Ph.D. thesis, University of Cape Town (1988).Google Scholar
[15]Labuschagne, L. E.. On the minimum modulus of an arbitrary linear operator. Quaestiones Math. 14 (1991), 77–91.CrossRefGoogle Scholar
[16]Lin, C. S.. Regularizers of closed operators. Canad. Math. Bull. 17 (1974), 67–71.CrossRefGoogle Scholar
[17]Mennicken, R. and Sagraloff, B.. Störungstheoretische Untersuchungen über Semi-Fredholmpaare und -operatoren in lokalkonvexen Vektorräumen II. J. Reine Angew. Math. 280 (1976), 1–36.Google Scholar
[18]Mennicken, R. and Sagraloff, B.. Störungstheoretische Untersuchungen über Semi-Fredholmpaare und -operatoren in lokalkonvexen Vektorräumen II. J. Reine Angew. Math. 303/304 (1978), 389–436.Google Scholar
[19]Pietsch, A.. Ein verallgemeinertes Spektralproblem für lineare Abbildungen in lokalkonvexen Vektorräumen. Math. Ann. 140 (1960), 147–152.CrossRefGoogle Scholar
[20]Pietsch, A.. Homomorphismen in lokalkonvexen Vektorräumen. Math. Nachr. 22 (1960), 162–174.CrossRefGoogle Scholar
[21]Pietsch, A.. Zur Theorie der σ-Transformationen in lokalkonvexen Vektorräumen. Math. Nachr. 21 (1960), 347–369.CrossRefGoogle Scholar
[22]Robertson, A. P. and Robertson, W. J.. Topological Vector Spaces, 2nd edition. Cambridge Tracts in Math. no. 53 (Cambridge University Press, 1973).Google Scholar
[23]van Dulst, D.. Perturbation theory and strictly singular operators in locally convex spaces. Studia Math. 38 (1970), 341–372.CrossRefGoogle Scholar
[24]Vladimirskii, Ju N.. On bounded perturbations ø─-operators in locally convex spaces. Soviet Math. Dokl. 12 (1971), 80–83.Google Scholar
[25]Vladimirskii, Ju N.. ø─-operators in locally convex spaces. Soviet Math. Dokl. 10 (1969), 99–102.Google Scholar