Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-18T08:41:40.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonsoluble length of finite groups with commutators of small order

Published online by Cambridge University Press:  13 February 2015

Y. CONTRERAS–ROJAS  and
PAVEL SHUMYATSKY
Y. CONTRERAS–ROJAS
Affiliation:
Department of Mathematics, University of Brasilia, Brasilia-DF, 70910-900Brazil. e-mail: Yerkocr@mat.unb.br
PAVEL SHUMYATSKY
Affiliation:
Department of Mathematics, University of Brasilia, Brasilia-DF, 70910-900Brazil. e-mail: pavel@unb.br
Get access Rights & Permissions [Opens in a new window]

Abstract

Let p be a prime. Every finite group G has a normal series each of whose quotients either is p-soluble or is a direct product of nonabelian simple groups of orders divisible by p. The non-p-soluble length λp(G) is defined as the minimal number of non-p-soluble quotients in a series of this kind.

We deal with the question whether, for a given prime p and a given proper group variety 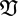, there is a bound for the non-p-soluble length λp of finite groups whose Sylow p-subgroups belong to 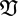. Let the word w be a multilinear commutator. In this paper we answer the question in the affirmative in the case where p is odd and the variety is the one of groups satisfying the law we ≡ 1.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 158 , Issue 3 , May 2015 , pp. 487 - 492
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Acciarri, C., Fernández-Alcober, G. A. and Shumyatsky, P.A focal subgroup theorem for outer commutator words. J. Group Theory 15 (2012), 397–405.Google Scholar
[2]Detomi, E., Morigi, M. and Shumyatsky, P.Bounding the exponent of a verbal subgroup. Ann. Mat. 193 (2014), 1431–1441.Google Scholar
[3]Feit, W. and Thompson, J. G.Solvability of groups of odd order. Pacific J. Math. 13 (1963), 773–1029.Google Scholar
[4]Hall, P. and Higman, G.The p-length of a p-soluble group and reduction theorems for Burnside's problem. Proc. London Math. Soc. (3) 6 (1956), 1–42.CrossRefGoogle Scholar
[5]Khukhro, E. I. and Shumyatsky, P. Nonsoluble and non-p-soluble length of finite groups. To appear in Israel J. Math.Google Scholar
[6]Khukhro, E. I. and Shumyatsky, P.Words and pronilpotent subgroups in profinite groups. J. Aust. Math. Soc. 97 (2014), 343–364.CrossRefGoogle Scholar
[7]Unsolved Problems in Group Theory. The Kourovka Notebook, no. 17, Institute of Mathematics (Novosibirsk, 2010).Google Scholar
[8]Liebeck, M. W., O' Brien, E. A., Shalev, A. and Tiep, P. H.The Ore conjecture. J. Eur. Math. Soc. (JEMS) 12 (2010), no. 4, 939–1008.Google Scholar
[9]Shumyatsky, P.Verbal subgroups in residually finite groups. Quart. J. Math. 51 (2000) 523–528.Google Scholar
[10]Shumyatsky, P.Commutators in residually finite groups. Israel J. Math. 182 (2011), 149–156.Google Scholar
[11]Shumyatsky, P.On the exponent of a verbal subgroup in a finite group. J. Aust. Math. Soc. 93 (2012), 325–332.Google Scholar
[12]Wilson, J.On the structure of compact torsion groups. Monatsh. Math. 96, 57–66.Google Scholar
[13]Zelmanov, E. I.On some problems of the theory of groups and Lie algebras. Mat. Sb. 180, 159–167; English transl. Math. USSR Sb. 66 (1990), 159–168.Google Scholar
[14]Zelmanov, E. I.A solution of the Restricted Burnside Problem for groups of odd exponent. Izv. Akad. Nauk SSSR Ser. Mat. 54, 42–59; English transl. Math. USSR Izvestiya. 36 (1991), 41–60.Google Scholar
[15]Zelmanov, E. I.A solution of the Restricted Burnside Problem for 2-groups. Mat. Sb. 182, 568–592; English transl. Math. USSR Sb. 72 (1992), 543–565.Google Scholar
[16]Zelmanov, E. I.On periodic compact groups. Israel J. Math. 77, no. 1–2 (1992), 83–95.Google Scholar