Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-28T22:07:38.605Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear random equations with maximal monotone operators in Banach spaces

Published online by Cambridge University Press:  24 October 2008

Dimitrios Kravvaritis
Dimitrios Kravvaritis
Affiliation:
Department of Mathematics, National Technical University of Athens, Patission 42, Greece
Get access Rights & Permissions [Opens in a new window]

Extract

Let X be a real Banach space, X* its dual space and ω a measurable space. Let D be a subset of X, L: Ω × D → X* a random operator and η:Ω →X* a measurable mapping. The random equation corresponding to the double [L, η] asks for a measurable mapping ξ: Ω → D such that

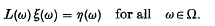
Random equations with operators of monotone type have been studied recentely by Kannan and Salehi [7], Itoh [6] and Kravvarits [8].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 98 , Issue 3 , November 1985 , pp. 529 - 532
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Browder, F. E.. Nonlinear operators and nonlinear equations of evolution in Banach spaces. Proc. Sympos. Pure Math. vol. 18, part 2 (Amer. Math. Soc, 1976).Google Scholar
[2]Browder, F. E.. Nonlinear maximal monotone operators in Banach space. Math. Ann. 175 (1968), 89–113.CrossRefGoogle Scholar
[3]Castaing, C. and Valadier, M.. Convex Analysis and Measurable Multifunctions. Lecture Notes in Math. vol. 580 (Springer-Verlag, 1977).CrossRefGoogle Scholar
[4]Dunford, N. and Schwarz, J. T.. Linear Operators, part I (Interscience, 1958).Google Scholar
[5]Himmlberg, C. J.. Measurable relations. Fund. Math. 87 (1975), 53–72.CrossRefGoogle Scholar
[6]Itoh, S.. Nonlinear random equations with monotone operators in Banach spaces. Math. Ann. 236(1978), 133–146.CrossRefGoogle Scholar
[7]Kannan, R. and Salehi, H.. Random nonlinear equations and monotonic nonlinearities. J. Math. Anal. Appl. 57 (1977), 234–256.CrossRefGoogle Scholar
[8]Kravvaritis, D.. Nonlinear random operators of monotone type in Banach spaces. J. Math. Anal. Appl. 78 (1980), 488–496.CrossRefGoogle Scholar
[9]Kuratowski, K. and Ryxl-Nabdzewski, C.. A general theorem on selectors. Bull. Acad.Polon. Sir. Sci. Math. Astronom. Phys. 13 (1965), 397–403.Google Scholar
[10]Trojanski, S. L.. On locally uniformly convex and differentiable norms in certain non-separable Banach spaces. Studia Math. 37 (1971), 173–180.CrossRefGoogle Scholar