Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-18T06:39:54.730Z Has data issue: false hasContentIssue false
  • English
  • Français

The Hilbert transform of Schwartz distributions. II

Published online by Cambridge University Press:  24 October 2008

M. Aslam Chaudhry  and
J. N. Pandey
M. Aslam Chaudhry
Affiliation:
Department of Mathematics, University of Petroleum and Minerals, Dhahran, Saudi Arabia
J. N. Pandey
Affiliation:
Department of Mathematics and Statistics, Carleton University, Ottawa, Ontario KIS 5B6, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

Let D(R) be the Schwartz space of C∞ functions with compact support on R and let H(D) be the space of all C∞ functions defined on R for which every element is the Hilbert transform of an element in D(R), i.e.

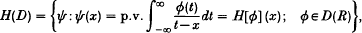
where the integral is defined in the Cauchy principal-value sense. Introducing an appropriate topology in H(D), Pandey [3] defined the Hilbert transform Hf of f ∈ (D(R))′ as an element of (H(D))′ by the relation

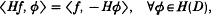
and then with an appropriate interpretation he proved that

.

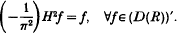In this paper we give an intrinsic description of the space H(D) and its topology, thereby providing a solution to an open problem posed by Pandey ([4], p. 90).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 553 - 559
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ehrenpreis, L.. Analytic functions and the Fourier transform of distributions. I. Ann. of Math. 63 (1956), 120–159.CrossRefGoogle Scholar
[2]Friedman, A.. Generalized Functions and Partial Differential Equations (Prentice-Hall, 1963).Google Scholar
[3]Pandey, J. N. and Chaudhry, M. A.. The Hilbert transform of generalized functions and applications. Canad. J. Math. 35 (1983), 478–495.CrossRefGoogle Scholar
[4]Pandey, J. N.. The Hilbert transform of Schwartz distributions. Proc. Amer. Math. Soc. 89 (1983), 86–90.CrossRefGoogle Scholar
[5]Schwartz, L.. Théorie des distributions (Hermann, 1966).Google Scholar
[6]Titchmarsh, E. C.. Introduction to the Theory of Fourier Integrals (Oxford University Press, 1967).Google Scholar
[7]Zemanian, A. H.. Distribution Theory and Transform Analysis (McGraw-Hill, 1965).Google Scholar
[8]Zemanian, A. H., Generalized Integral Transforms (Interscience Publishers, 1968).Google Scholar