Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mason, R. C.
1986.
Norm form equations. III: positive characteristic.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 99,
Issue. 3,
p.
409.
Frey, Gerhard
1987.
Séminaire de Théorie des Nombres, Paris 1985–86.
Vol. 71,
Issue. ,
p.
39.
Frey, Gerhard
1989.
Number Theory.
Vol. 1380,
Issue. ,
p.
31.
Mueller, J.
1990.
Analytic Number Theory.
p.
383.
Van Der Poorten, A. J.
and
Schlickewei, H. P.
1991.
Additive relations in fields.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 51,
Issue. 1,
p.
154.
Browkin, J.
and
Brzeziński, J.
1994.
Some remarks on the 𝑎𝑏𝑐-conjecture.
Mathematics of Computation,
Vol. 62,
Issue. 206,
p.
931.
Wooley, Trevor D.
1994.
Quasi-diagonal behaviour in certain mean value theorems of additive number theory.
Journal of the American Mathematical Society,
Vol. 7,
Issue. 1,
p.
221.
Wang, Julie
1996.
𝑆-integral points of ℙⁿ-{2𝕟+1 hyperplanes in general position over number fields and function fields}.
Transactions of the American Mathematical Society,
Vol. 348,
Issue. 8,
p.
3379.
Bombieri, Enrico
and
Mueller, Julia
1998.
On a conjecture of Siegel.
Monatshefte f�r Mathematik,
Vol. 125,
Issue. 4,
p.
293.
Ferguson, Helaman
Bailey, David
and
Arno, Steve
1999.
Analysis of PSLQ, an integer relation finding algorithm.
Mathematics of Computation,
Vol. 68,
Issue. 225,
p.
351.
Tzu-Yueh Wang, Julie
1999.
Integral Points of Projective Spaces Omitting Hyperplanes over Function Fields of Positive Characteristic.
Journal of Number Theory,
Vol. 77,
Issue. 2,
p.
336.
Browkin, Jerzy
2000.
Number Theory.
p.
75.
Browkin, Jerzy
2000.
Number Theory.
p.
75.
Ru, Min
2000.
A Weak Effective Roth's Theorem over Function Fields.
Rocky Mountain Journal of Mathematics,
Vol. 30,
Issue. 2,
Hu, Pei‐Chu
and
Yang, Chung‐Chun
2002.
A note on the abc conjecture.
Communications on Pure and Applied Mathematics,
Vol. 55,
Issue. 9,
p.
1089.
Pintér, Á.
2002.
Zeros of the sum of polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 270,
Issue. 1,
p.
303.
Ru, Min
and
Wang, Julie
2003.
Truncated second main theorem with moving targets.
Transactions of the American Mathematical Society,
Vol. 356,
Issue. 2,
p.
557.
Fuchs, Clemens
Pethő, Attila
and
Tichy, Robert
2003.
On the Diophantine equation 𝐺_{𝑛}(𝑥)=𝐺_{𝑚}(𝑃(𝑥)): Higher-order recurrences.
Transactions of the American Mathematical Society,
Vol. 355,
Issue. 11,
p.
4657.
Hsia, Liang-Chung
and
Wang, Julie
2003.
The ABC theorem for higher-dimensional function fields.
Transactions of the American Mathematical Society,
Vol. 356,
Issue. 7,
p.
2871.
Vaserstein, L. N.
and
Wheland, E. R.
2003.
Vanishing Polynomial Sums.
Communications in Algebra,
Vol. 31,
Issue. 2,
p.
751.
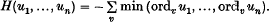
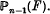 .
.

