Article contents
Random symmetric matrices: rank distribution and irreducibility of the characteristic polynomial
Published online by Cambridge University Press: 12 May 2022
Abstract
Conditional on the extended Riemann hypothesis, we show that with high probability, the characteristic polynomial of a random symmetric
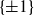 $\{\pm 1\}$
-matrix is irreducible. This addresses a question raised by Eberhard in recent work. The main innovation in our work is establishing sharp estimates regarding the rank distribution of symmetric random
$\{\pm 1\}$
-matrix is irreducible. This addresses a question raised by Eberhard in recent work. The main innovation in our work is establishing sharp estimates regarding the rank distribution of symmetric random
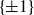 $\{\pm 1\}$
-matrices over
$\{\pm 1\}$
-matrices over
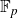 $\mathbb{F}_p$
for primes
$\mathbb{F}_p$
for primes
 $2 < p \leq \exp(O(n^{1/4}))$
. Previously, such estimates were available only for
$2 < p \leq \exp(O(n^{1/4}))$
. Previously, such estimates were available only for
 $p = o(n^{1/8})$
. At the heart of our proof is a way to combine multiple inverse Littlewood–Offord-type results to control the contribution to singularity-type events of vectors in
$p = o(n^{1/8})$
. At the heart of our proof is a way to combine multiple inverse Littlewood–Offord-type results to control the contribution to singularity-type events of vectors in
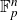 $\mathbb{F}_p^{n}$
with anticoncentration at least
$\mathbb{F}_p^{n}$
with anticoncentration at least
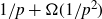 $1/p + \Omega(1/p^2)$
. Previously, inverse Littlewood–Offord-type results only allowed control over vectors with anticoncentration at least
$1/p + \Omega(1/p^2)$
. Previously, inverse Littlewood–Offord-type results only allowed control over vectors with anticoncentration at least
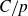 $C/p$
for some large constant
$C/p$
for some large constant
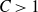 $C > 1$
.
$C > 1$
.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 2 , March 2023 , pp. 233 - 246
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
Footnotes
Supported in part by NSF grants DMS-1954395 and DMS-1953799.
Sah and Sawhney were supported by NSF Graduate Research Fellowship Program DGE-1745302.
References
REFERENCES
- 4
- Cited by


