No CrossRef data available.
Article contents
Pestov's identity on frame bundles and applications
Published online by Cambridge University Press: 29 April 2016
Abstract
In this paper we lift Pestov's Identity on the tangent bundle of a Riemannian manifold M to the bundle of k-tuples of tangent vectors. We also derive an integrated version and a restriction to the frame bundle PkM of k-frames. Finally, we discuss a dynamical application for the parallel transport on 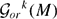 $\cal{G}_{or}^{k} (M)$, the Grassmannian of oriented k-planes of M.
$\cal{G}_{or}^{k} (M)$, the Grassmannian of oriented k-planes of M.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 161 , Issue 2 , September 2016 , pp. 357 - 377
- Copyright
- Copyright © Cambridge Philosophical Society 2016


