Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-25T05:59:25.827Z Has data issue: false hasContentIssue false
  • English
  • Français

On the quotients of mapping class groups of surfaces by the Johnson subgroups

Part of: Homotopy theory

Published online by Cambridge University Press:  27 November 2019

TOMÁŠ ZEMAN Open the ORCID record for TOMÁŠ ZEMAN [Opens in a new window]
TOMÁŠ ZEMAN*
Affiliation:
Postal Address: Mathematical Institute, Woodstock Road, Oxford, OX2 6GG. (Previous e-mail: tomas.zeman@maths.ox.ac.uk) Current Address: Dept. of Mathematics, Stockholm University, SE - 106 91 Stockholm, Sweden. e-mail: tomas.zeman@math.su.se
Get access Rights & Permissions [Opens in a new window]

Abstract

We study quotients of mapping class groups 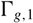${\Gamma _{g,1}}$ of oriented surfaces with one boundary component by the subgroups 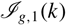${{\cal I}_{g,1}}(k)$ in the Johnson filtrations, and we show that the stable classifying spaces 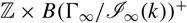${\mathbb {Z}} \times B{({\Gamma _\infty }/{{\cal I}_\infty }(k))^ + }$ after plus-construction are infinite loop spaces, fitting into a tower of infinite loop space maps that interpolates between the infinite loop spaces ${\mathbb {Z}} \times B\Gamma _\infty ^ + $ and ${\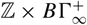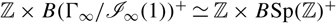mathbb {Z}} \times B{({\Gamma _\infty }/{{\cal I}_\infty }(1))^ + } \simeq {\mathbb {Z}} \times B{\rm{Sp}}{({\mathbb {Z}})^ + }$ . We also show that for each level k of the Johnson filtration, the homology of these quotients with suitable systems of twisted coefficients stabilises as the genus of the surface goes to infinity.

MSC classification

Primary: 57S05: Topological properties of groups of homeomorphisms or diffeomorphisms
Secondary: 55P47: Infinite loop spaces
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 170 , Issue 2 , March 2021 , pp. 355 - 377
Copyright
© Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andreadakis, S.. On the automorphisms of free groups and free nilpotent groups. Proc. London Math. Soc. 3.15 (1965), pp. 239–268.CrossRefGoogle Scholar
Basterra, M., Bobkova, I., Ponto, K., Tillmann, U. and Yeakel, S.. Infinite loop spaces from operads with homological stability. Adv. Math. 321 (2017), pp. 391–430.CrossRefGoogle Scholar
Borel, A.. Stable real cohomology of arithmetic groups. Ann. Sci. École Norm. Sup. (4), 7 (1974), 235–272.CrossRefGoogle Scholar
Borel, A.. Stable real cohomology of arithmetic groups II. Manifolds and Lie groups: papers in honor of Yozo Matsushima. Progr. Math. 14 (Birkhäuser, 1981), pp. 21–55.CrossRefGoogle Scholar
Brown, K. S.. Cohomology of groups. Graduate Texts in Mathematics 87 (Springer-Verlag, 1982).CrossRefGoogle Scholar
Charney, R.. A generalization of a theorem of Vogtmann. Pure Appl. Alg. 44.1 (1987), pp. 107–125.CrossRefGoogle Scholar
Church, T. and Ellenberg, J. S.. Homology of FI-modules. Geom. Topol. 21.4 (2017), pp. 2373–2418.CrossRefGoogle Scholar
Church, T., Ellenberg, J. S. and Farb, B.. FI-modules and stability for representations of symmetric groups. Duke Math. J. 164.9 (2015), pp. 1833–1910.CrossRefGoogle Scholar
Church, T., Ellenberg, J. S., Farb, B. and Nagpal, R.. FI-modules over Noetherian rings. Geom. Topol. 18.5 (2014), pp. 2951–2984.CrossRefGoogle Scholar
Church, T. and Putman, A.. Generating the Johnson filtration. Geom. Topol. 19.4 (2015), pp. 2217–2255.CrossRefGoogle Scholar
Dehn, M.. Papers on Group Theory and Topology. Trans. German by John Stillwell (Springer-Verlag, 1987).CrossRefGoogle Scholar
Farb, B. and Margalit, D.. A primer on mapping class groups. Princeton Mathematical Series 49 (Princeton University Press, 2012).CrossRefGoogle Scholar
Harer, J. L.. Stability of the homology of the mapping class groups of orientable surfaces. Ann. of Math. (2) 121.2 (1985), pp. 215–249.CrossRefGoogle Scholar
Johnson, D.. A survey of the torelli group. Low-dimensional topology (Proceedings of the Special Session held at the 87th Annual Meeting of the American Mathematical Society, San Francisco, California, January 1981). Ed. by Samuel, J. Lomonaco Jr Contemp. Math. 20 (1983).Google Scholar
Johnson, D.. The structure of the torelli group—II: a characterization of the group generated by twists on bounding curves. Topology 24.2 (1985), pp. 113–126.CrossRefGoogle Scholar
Kawazumi, N. and Morita, S.. The primary approximation to the cohomology of the moduli space of curves and cocycles for the stable characteristic classes. Math. Res. Lett. 3.5 (1996), 629–641.CrossRefGoogle Scholar
Mac Lane, S.. Categorical algebra. Bull. Amer. Math. Soc. 71.1 (1965).CrossRefGoogle Scholar
Madsen, I. and Weiss, M.. The stable moduli space of Riemann surfaces: Mumford’s conjecture. Ann. of Math. (2) 165.3 (2007), pp. 843–941.CrossRefGoogle Scholar
McDuff, D. and Segal, G.. Homology fibrations and the “group-completion” theorem. Invent. Math. 31 (1976), pp. 279–284.CrossRefGoogle Scholar
Patzt, P.. Representation stability for filtrations of torelli groups. Math. Ann. 372 (1–2) (2018), pp. 257–298.CrossRefGoogle Scholar
Putman, A. and Sam, S.. Representation stability and finite linear groups. Duke Math. J. 166.13 (2017), pp. 2521–2598.CrossRefGoogle Scholar
Randal–Williams, O. and Wahl, N.. Homological stability for automorphism groups. Adv. Math. 318 (2017), pp. 534–626.CrossRefGoogle Scholar
Serre, J.-P.. Lie algebras and Lie groups. Lecture Notes in Math. 1500 (Springer, 2006).Google Scholar
Szymik, M.. The rational stable homology of mapping class groups of universal nil-manifolds. To appear in Annales de l’Institut Fourier; arXiv:1605.06508 (2016).Google Scholar
Szymik, M.. Twisted homological stability for extensions and automorphism groups of free nilpotent groups. Journal of K-theory: K-theory and its Applications to Algebra, Geometry and Topology, 14.1 (2014), pp. 185–201.CrossRefGoogle Scholar
Tillmann, U.. Higher genus surface operad detects infinite loop spaces. Math. Ann. 317.3 (2000), pp. 613–628.CrossRefGoogle Scholar
Tillmann, U.. On the homotopy of the stable mapping class group. Invent. Math. 130.2 (1997), pp. 257–275.CrossRefGoogle Scholar
Wahl, N.. From mapping class groups to automorphism groups of free groups. J. London Math. Soc. (2) 72.2 (2005), pp. 510–524.CrossRefGoogle Scholar
Wahl, N.. Infinite loop space structure(s) on the stable mapping class group. Topology 43.2 (2004), pp. 343–368.CrossRefGoogle Scholar
Weibel, C.. An introduction to homological algebra. Camb. Stud. Adv. Math. 38 (Cambridge University Press, 1994).CrossRefGoogle Scholar
Zeman, T.. Operads with homological stability and infinite loop space structures. In preparation.Google Scholar