On summability domains
Published online by Cambridge University Press: 24 October 2008
Extract
We denote by ω the space of all complex sequences with the topology given by the semi-norms
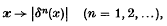
where δn(x) = xn. An FK-space, E, is a subspace of ω on which there exists a complete metrizable locally convex topology τ, such that the inclusion (E, τ) ⊂ ω is continuous; if τ is given by a single norm then E is a BK-space.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 73 , Issue 2 , March 1973 , pp. 327 - 338
- Copyright
- Copyright © Cambridge Philosophical Society 1973
References
REFERENCES
- 3
- Cited by


