Linear forms in algebraic points of Abelian functions. II
Published online by Cambridge University Press: 24 October 2008
Extract
In this paper we continue to develop the apparatus needed for the proof of the theorem announced in (11). We retain the notation of (11) together with the assumptions made there about the field 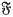 of Abelian functions. This section deals with properties of more general functions holomorphic on Cn. When n = 1 the extrapolation procedure in problems of transcendence is essentially the maximum modulus principle together with the act of dividing out zeros of an analytic function. For n > 1, however, this approach is not possible, and some mild theory of several complex variables is required. This was first used in the context of transcendence by Bombieri and Lang in (2) and (12), and we now give a brief account of the basic constructions of their papers.
of Abelian functions. This section deals with properties of more general functions holomorphic on Cn. When n = 1 the extrapolation procedure in problems of transcendence is essentially the maximum modulus principle together with the act of dividing out zeros of an analytic function. For n > 1, however, this approach is not possible, and some mild theory of several complex variables is required. This was first used in the context of transcendence by Bombieri and Lang in (2) and (12), and we now give a brief account of the basic constructions of their papers.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 79 , Issue 1 , January 1976 , pp. 55 - 70
- Copyright
- Copyright © Cambridge Philosophical Society 1976
References
REFERENCES
- 1
- Cited by


