Other
Index to Volume 106 Numbers 565 to 567
-
- Published online by Cambridge University Press:
- 21 February 2023, pp. i-ix
-
- Article
-
- You have access
- Export citation
Articles
Fibonacci Fraction Circles
-
- Published online by Cambridge University Press:
- 24 February 2022, pp. 1-8
-
- Article
- Export citation
Dropping plates
-
- Published online by Cambridge University Press:
- 22 June 2022, pp. 193-205
-
- Article
- Export citation
Focus on the Visual (The 2022 Presidential Address)
-
- Published online by Cambridge University Press:
- 12 October 2022, pp. 386-399
-
- Article
- Export citation
Other
MA Presidential Blog
-
- Published online by Cambridge University Press:
- 24 February 2022, p. 8
-
- Article
- Export citation
Articles
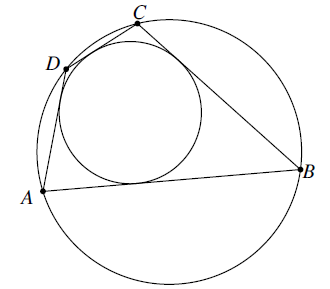
An extension of the six-point circle theorem for a generalised Van Aubel configuration
-
- Published online by Cambridge University Press:
- 12 October 2022, pp. 400-407
-
- Article
- Export citation
The real solutions of x = ax
-
- Published online by Cambridge University Press:
- 22 June 2022, pp. 206-211
-
- Article
- Export citation
Golden right triangles and the golden quadrilateral
-
- Published online by Cambridge University Press:
- 24 February 2022, pp. 9-20
-
- Article
- Export citation
Approximating the volume of a solid of revolution – the frustum rule
-
- Published online by Cambridge University Press:
- 12 October 2022, pp. 408-413
-
- Article
- Export citation
Winning strategies: the emergence of base 2 in the game of nim
-
- Published online by Cambridge University Press:
- 22 June 2022, pp. 212-219
-
- Article
- Export citation
A mathematical approximation in the physical sciences
-
- Published online by Cambridge University Press:
- 22 June 2022, pp. 220-232
-
- Article
- Export citation
New characterisations of bicentric quadrilaterals
-
- Published online by Cambridge University Press:
- 12 October 2022, pp. 414-426
-
- Article
- Export citation
The trisectrix and Langley's problem
-
- Published online by Cambridge University Press:
- 24 February 2022, pp. 21-27
-
- Article
- Export citation
A computer look at N!
-
- Published online by Cambridge University Press:
- 22 June 2022, pp. 233-241
-
- Article
- Export citation
Two short proofs of the formula
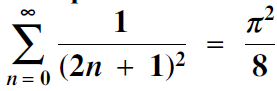 $\sum\limits_{n = 0}^\infty {{1 \over {{{(2n + 1)}^2}}} = {{{\pi ^2}} \over 8}} $
$\sum\limits_{n = 0}^\infty {{1 \over {{{(2n + 1)}^2}}} = {{{\pi ^2}} \over 8}} $
-
- Published online by Cambridge University Press:
- 24 February 2022, pp. 28-31
-
- Article
- Export citation
Archimedes playing with a computer
-
- Published online by Cambridge University Press:
- 12 October 2022, pp. 427-442
-
- Article
- Export citation
An index for betting with examples from games and sports
-
- Published online by Cambridge University Press:
- 24 February 2022, pp. 32-40
-
- Article
- Export citation
Evolution of the Euler-Maclaurin sum formula
-
- Published online by Cambridge University Press:
- 12 October 2022, pp. 443-457
-
- Article
- Export citation
Fibonacci-Lucas hyperbolas
-
- Published online by Cambridge University Press:
- 22 June 2022, pp. 242-246
-
- Article
- Export citation
Locus problems concerning centroids of a cyclic quadrilateral and two classic cubic curves
-
- Published online by Cambridge University Press:
- 22 June 2022, pp. 247-257
-
- Article
-
- You have access
- Open access
- Export citation

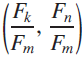
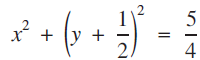
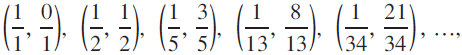

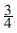
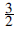

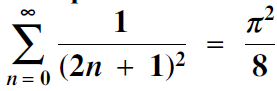
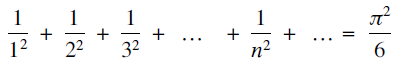
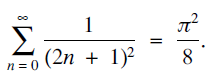
 ) or (
) or (