No CrossRef data available.
Published online by Cambridge University Press: 14 June 2016
Consider the integral
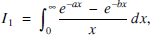
where b > a > 0. First, let us clarify why it even exists. Of course, convergence at infinity is ensured by the exponential terms, but the integrals of and e–ax/x and e–bx/x, taken separately, are divergent at 0, since these integrands equate asymptotically to 1/x as x → 0. However,
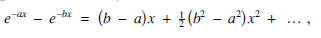
so (e–ax – e–bx)/x tends to the finite limit b – a as x → 0 and there is no problem integrating it on intervals of the form [0, r].
A neat way to evaluate I1 starts by expressing the integrand itself as an integral:
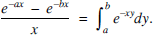 (1)
(1)
Inserting this into I1 converts it into a double integral.