Article contents
Identities connecting the Chebyshev polynomials
Published online by Cambridge University Press: 17 October 2016
Extract
There are many families of polynomials in mathematics, and they often occur naturally in pairs. The Fibonacci polynomials and the Lucas polynomials, for example, are generated by the same recurrence relation but with different starting values, and there are many identities that link the two families [1]. The same is true for the Chebyshev polynomials of the first and second kinds, Tn (x) and Un (x) [2], respectively. There are two further polynomial families that are less well-known, the Chebyshev polynomials of the third and fourth kinds, Vn (x) and Wn (x) [3], respectively. Each of the four kinds is an example of an orthogonal polynomial family Pn (x), where for some appropriate weight function W (x), 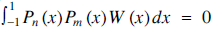 whenever n ≠ m. The families Tn (x) and Un (x) in particular are ubiquitous in their mathematical uses, in approximation theory, in differential equations, and in solving the Pell equation, to name but three. There are also many connections between Tn (x), Un (x), Vn (x) and Wn (x), some of which are explored here, and some of which we hope are new.
whenever n ≠ m. The families Tn (x) and Un (x) in particular are ubiquitous in their mathematical uses, in approximation theory, in differential equations, and in solving the Pell equation, to name but three. There are also many connections between Tn (x), Un (x), Vn (x) and Wn (x), some of which are explored here, and some of which we hope are new.
- Type
- Articles
- Information
- Copyright
- Copyright © Mathematical Association 2016
References
- 1
- Cited by


