1 Introduction
The decade 1992-2002 in semiconductor optics can be called “decade of microcavities”. Hundreds if not thousands of papers dedicated to the physics of light-matter interaction in microcavities have appeared. Still, cavities remain one of the most intriguing semiconductor systems, extremely rich with new fundamental effects. Among such effects, we can mention the strong coupling of photons and excitons, the optical coupling of macroscopically separated quantum wells, giant Faraday rotation, motional narrowing and stimulated scattering of exciton-polaritons, their weak localization and their Bose-condensation. Many laboratories all over the world now work on enhancing the growth of microcavity samples, whose which is perpetually on the increase. All kinds of available optical spectroscopy techniques have been applied to study the properties of exciton-polaritons in microcavities. The observed phenomena are still puzzling theorists involved in these studies.
We do not claim to assemble a comprehensive story of microcavities physics from start to finish, not to mention that the story itself is far from over. We try to give here an overview of the first decade of the “microcavity boom”.
Our point of view on the theory of cavity polaritons can be briefly formulated as follows: We suppose that the most natural and simple way to interpret optical effects (all effects connected with the polaritons are optical effects) is to recourse to classical optics. We will avoid in this paper the unnecessary use of quantum mechanics and will consider light interaction with excitons in terms of Maxwell equations written for a system having a non-local dielectric response function. We are convinced that the language of classical optics is the one most adapted to description of coherent optical spectra (reflection, transmission and resonant elastic scattering spectra), and can be successfully applied to interpret a number of non-linear effects in cavities. We will only use the alternative formalism of quantum electrodynamics when talking about Bose-condensation of exciton-polaritons and perspectives on the realization of the polariton laser.
Historically, studies of microcavities have been started by reflectivity measurements that reveal the strong coupling between the exciton resonance and the confined cavity mode (Weisbuch, 1992 Reference Weisbuch, Nishioka, Ishikawa and Arakawa[1]). This is why we begin this paper with a careful calculation of light reflection by the basic elements of a microcavity, namely, Bragg mirrors and quantum wells. We introduce the exciton-polaritons in quantum wells following the works of Andreani, Bassani and Ivchenko (1980s Reference Andreani, Burstein and Weisbuch[2] Reference Andreani, Tassone and Bassani[3] Reference Ivchenko[4]). Using the transfer matrix formalism we show how to obtain the dispersion equations for exciton-polaritons in microcavities.
Then we focus on the most recent experimental data on the dynamics of energy relaxation of exciton-polaritons in microcavities. Observation of stimulated scattering of exciton-polaritons by Savvidis et al (2000) Reference Savvidis, Baumberg, Stevenson, Skolnick, Whittaker and Roberts[5] has opened a new field that is attacting a huge number of experimental groups and theorists. Bosonic behavior of polaritons, evidenced in the experiments of Baumberg and his collaborators inspired many speculations on the possibility of the realisation of a new generation of opto-electronic devices, polariton lasers, lasers which do not require inversion of population. We shall carefully describe all the main mechanisms of polariton relaxation in the cavities, namely, scattering with acoustic and optical phonons, polariton-polariton and polariton-electron scattering. The famous “bottleneck” problem that prevents realization of polariton lasers will be addressed. Finally, we give a simple theory of polariton Bose condensation in a finite two-dimensional system and discuss a possibility of realisation of a polariton laser.
We have limited our scope to microcavities in the strong coupling regime only. For all effects connected with vertical cavity surface emitting lasers (VCSELs) or light-emitting diods (VCLEDs) the reader is referred to the vast literature existing on the subject.
2 How typical microcavities look
A typical microcavity structure is schematically shown on figure 1. It consists of a planar Fabry-Perot cavity sandwiched between two so-called Bragg mirrors and containing an embedded quantum well (QW) (figure 1a), or, possibly, a thin layer of bulk semiconductor, multiple QWs (figure 1b), quantum wires or quantum dots. A Bragg mirror is a periodical structure made up of two semiconductor or dielectric materials having different refractive indices. The thicknesses of layers are chosen so that the light reflected by all the interfaces interferes negatively within a spectral range further referred to as the stop-band. In high-quality structures, reflectivity of Bragg mirrors within the stop-band exceeds 99%. Their spectral width is 100 meV wide. The thickness of the cavity layer usually ranges from one to three times the wavelength of light in the center of the stop-band. A so-called cavity mode, i.e. a light-mode confined in the cavity, has a finesse dependent on the reflectivity of the mirrors. It can be as high as 1500-2000 in the best samples. In quantum microcavities the parameters of Bragg mirrors and cavity are chosen to have a resonance between the cavity mode frequency and the exciton transition in a quantum structure embedded into the cavity. We recall that excitons are Coulomb-correlated electron-hole pairs characterized by discrete transition frequencies. Effects originating from coupling of the exciton resonance to the cavity mode are referred to as exciton-polariton effects where an exciton-polariton is a half-light-half-matter crystal excitation, a quasi-particle combining properties of excitons and photons.

Figure 1. Typical microcavity structures. The central cavity layer having a thickness equal to an integer number of half-wave-lengths of light at the exciton resonance frequency is sandwiched between two Bragg mirrors. A quantum well (a), or several quantum wells (b) are embedded at the antinodes of the cavity mode electric field in order to provide the strongest coupling to light.
Exciton-polaritons, predicted theoretically by Hopfield Reference Hopfield[6] and by Agranovich Reference Agranovich[7] Reference Agranovich and Ginzburg[8] in the beginning of 1960s, have been extensively studied in bulk semiconductor materials, thin films Reference Frolich, Kulik, Uebbing, Mysyrowicz, Langer, Stolz and von der Osten[9] Reference Panzarini and Andreani[10], quantum wells Reference Hanamura[11] Reference Citrin[12], quantum wires and dots Reference Gammon, Snow, Shanabrook, Katzer and Park[13] Reference Ivchenko and Kavokin[14]. They can be interpreted as virtual exciton-photon pairs that propagate through the crystal because of a chain of virtual absorptions and emissions of photons by excitons. It is essential to note that the polariton states are true eigen-states of the system, so that once polaritons are present, there are no more pure excitons or photons. Though the original theory of exciton-polaritons was written with the formalism of second quantization, it has been quickly understood that the so-called semi-classical approach is formally equivalent to the quantum description for any linear optical problem. Within the semi-classical approach, which will be used in most of this paper, the Maxwell equations are solved for light propagating within a dielectric media characterized by frequency-dependent (and eventually wave-vector-dependent) complex polarization induced by excitons. Dispersion of exciton-polaritons in this case is nothing but dispersion of light modified by the presence of the exciton resonance. The semi-classical technique is very suitable for the calculation of coherent optical spectra (reflection, transmission, and elastic scattering), although it hardly describes the energy relaxation and dephasing of exciton-polaritons.
Exciton-polaritons in microcavities have very particular properties resulting from the reduced dimensionality of the system with respect to semiconductor structures with no optical confinement. In particular, the strength of exciton-light coupling is greatly enhanced in microcavities, which results in so-called strong-coupling regime manifested by anticrossing of the exciton-polariton modes observed for the first time by Claude Weisbuch et al Reference Weisbuch, Nishioka, Ishikawa and Arakawa[1] in 1992. The sample chosen for this experiment was spatially inhomogeneous in the plane, thus providing experimentalists with an opportunity to tune the cavity mode to the exciton resonance by changing the light spot's position on the surface of the sample. They found a point of exact resonance between the light-mode and the exciton resonance where the reflection spectrum exhibited two distinct dips corresponding to two exciton-polariton eigen-modes of the microcavity. Figure 2 shows a series of reflection spectra calculated for a GaN-based microcavity sample similar to one studied studied in Ref. Reference Weisbuch, Nishioka, Ishikawa and Arakawa[1], except that it is GaN-based instead of GaAs-based. These eigen-modes appeared to split at the anticrossing point that defines the strong-coupling regime. Splitting between modes at this point is widely referred to as vacuum field Rabi-splitting or simply Rabi-splitting, although originally the term Rabi-splitting was used in atomic physics for a different effect. Note that in the opposite case of the weak-coupling regime, there is no splitting between polariton eigen-modes at the crossing point. The weak-coupling regime is achieved, in particular, in VCSELs and VCLEDs.

Figure 2. Reflection spectra of a GaN-based microcavity calculated for different detunings between the cavity mode and the exciton resonance. One can clearly show the anti-crossing of the polariton eigen states.
In this paper we will only discuss the phenomena characteristic of the strong coupling regime. Among these phenomena we should mention first of all the particular dependence of the polariton eigen-frequencies of the in-plane wave-vector of the incident light. This dependence further referred to as in-plane dispersionof cavity polaritons has been experimentally measured by angle-resolved reflection by Houdré et al Reference Houdre, Stanley, Oesterle, Ilegems, Weisbuch and de Physique[15]. It has been shown that the shape of polariton despersion curves is strongly dependent on the detuning between bare cavity mode ωc(k) and bare exciton mode ω0(k) at zero in-plane wave-vector k=0. The detuning is given by ωc(0) − ω0(0). Figure 3 shows three typical dispersion curves of cavity polaritons calculated for positive, zero, and negative detunings and for a GaN-based microcavity containing 9 QWs. One can see that at small k, dispersion of exciton-polaritons in the cavity is essentially parabolic and can be characterized by an effective mass, while this mass varies dramatically as a function of detuning. The possibility to tune the polariton's effective mass over a wide range is an important peculiarity of microcavities.

Figure 3. Energy versus in-plane wave vector for the excitonpolariton modes in a GaN-based microcavity similar to the one described in ref [68] for the cases of positive (a), zero (b), and negative (c) detuning between the cavity photon mode frequency and the exciton resonance.
Between 1992 and 2002 a variety of microcavity structures have been studied. Observed Rabi-splittings reached almost 30 meV in the best inorganic cavities and an order of magnitude larger in organic cavities. External magnetic field has been shown to increase the polariton splitting. Microcavities containing layers of bulk semiconductor, multiple QWs, quantum wires and dots, as well as coupled microcavities, pillar microcavities, photonic cavities have been studied. Some of these structures offering new optical effects are treated in this paper. Conventional microcavities with embedded QWs have shown the greatest number of interesting phenomena. In the end of 1990s, the scientific community enthusiastically discussed so-called motional narrowingeffect Reference Whittaker[16] Reference Kavokin[17] initially associated with observed narrowing of polariton spectral resonances in the vicinity of the anticrossing point. Further deep studies of the disorderscattering of cavity polaritons helped to understand the dynamics of these unusual quasi-particles.
2000 was a revolutionary year in the physics of microcavities. In the beginning of that year, research groups from Southampton and Sheffield reported observations of very strong stimulatedscattering of exciton-polaritons which evidenced that polaritons behave as good bosons and can, in principle, Bose-condense Reference Savvidis, Baumberg, Stevenson, Skolnick, Whittaker and Roberts[5]. Numerous works devoted to relaxation dynamics of polaritons in microcavities followed this discovery. The challenge has been to observe Bose-condensation of exciton-polaritons, an extremely fascinating effect likely to be exploited in future polariton lasers Reference Imamoglu, Ram, Pau and Yamamoto[18] Reference Imamoglu and Ram[19]. At the moment of submission of this manuscript we are aware of only few works claiming experimental evidence of polariton lasing Reference Huang, Yamamoto, André, Bleuse, Muller and Ulmer-Tuffigo[20] Reference Deng, Weihs, Santori, Bloch and Yamamoto[21]. New materials should necessarily come into play in order to allow for Bose-condensation of exciton-polaritons at room temperature.
We estimate potentialities of microcavities both for the basic studies and applications as very high. Much has to be done to understand quantum kinetics of exciton-polaritons and their spin-relaxation mechanisms. Intriguing consequences of Bose-condensation of polaritons, such as the optical Josephson effect Reference Aihara and Iida[22], to give an example, are awaiting for investigation. Our knowledge about microcavity polaritons is far from being complete; its improvement is certainly in the hands of the reader.
3 Reflection and transmission of light by quantum wells containing excitons
Here we derive amplitude reflection and transmission coefficients for light incident on a quantum well in the vicinity of the exciton resonance frequency.
3.1 Normal incidence case
Let us consider a light-wave propagating in dielectric media homogeneous in the plane of the wave (xy-plane) but possibly inhomogeneous in the propagation direction (z-direction). Electric

where
where
where k0=ω0/c is the wave-vector of light in vacuum.
In the local model:
where χ(z) is the localdielectric susceptibility. This simplest model of all can be successfully applied for description of cw experiments in QWs. It fails to describe correctly the dynamics of exciton-polaritons in quantum structures. Thus for the purposes of this paper it is not suitable. The reader can find a detailed description of the local model applied both to QWs and superlattices in the book by Ivchenko and Pikus Reference Ivchenko and Pikus[23].
In the rest of this section we will follow so-called non-local dielectric response theory developed by Andreani, Bassani and Ivchenko in 1980s to describe the optical response of excitons in QWs Reference Andreani, Burstein and Weisbuch[2] Reference Andreani, Tassone and Bassani[3] Reference Ivchenko[4]. It takes into account the fact that if an exciton appears at the point z′ of the crystal, the dielectric polarization is changed at all points z within the exciton wave-function. This effect is conveniently described in framework of the theory of spatial dispersion in the optical media, where the exciton wavefunction plays the role of the correlation function. This theory is based on an assumption that the exciton-induced dielectric polarization can be written in form:
where
with
Here Φ(z) is the exciton wavefunction taken with equal electron and hole coordinates (thus, z is the coordinate of both electron and hole), ω is the frequency of the incident light, γ is the homogeneousbroadening of the exciton resonance caused by acoustic phonons, ωLT and aB are two intrinsic excitonic parameters called longitudinal-transversesplitting and Bohr radius. Physically, the exciton Bohr radius is analogous to the hydrogen atom's Bohr radius, it is proportional to the average distance between electron and hole for the ground exciton state. aB in GaAs is 150Å, in wide-band semiconductors it is 2-4 times less. ωLT is a measure of exciton-light coupling strength in bulk semiconductors. For the ground exciton state in GaAs hωLT =0.08 meV, while in wide-band-gap materials (GaN, ZnO) it is an order of magnitude larger. Equation (3.6) is based on a micro-model described in detail by Haug and Koch Reference Haug and Koch[24].
Once the polarization (3.5) is introduced, Equation (3.3) becomes an integro-differential equation and can be solved exactly with use of the Green-function method. Within this method solution of Equation (3.3) is represented in a form
where E 0 is the amplitude of the incident light. The Green-function G is subject to the equation
Having in mind that
Equation (3.7) still should be solved with respect to E(z) which appears in both the left and right parts. In order to do so, let us multiply both parts by Φ(z) and integrate over z. This procedure leads to:
which means that
Now we come back to Equation (3.7) and substitute (3.11) into its right part:

Using (3.9) we finally obtain

Now the amplitude reflection (r) and transmission (t) coefficients of the QW can be obtained as:
If we consider a ground exciton state, Φ(z) is an even function, and the integrals in the right part of Equation (3.13) can be easily simplified.
In the limit of z->+∞:
in the limit of z>−∞:
This allows to obtain reflection and transmission coefficients of the QW in a simple and elegant form:
where
is an important characteristic further referred to as the exciton radiative broadening, and
is the renormalisation of the exciton resonance frequency due to the polariton effect.
The radiative broadening Γ0 is connected to the exciton radiative lifetime τthrough the relation
A finite exciton radiative lifetime is a particularity of confined electronic systems. In an infinite bulk crystal, an exciton-polariton can freely propagate in any direction and its lifetime is limited only by non-radiative processes like scattering with acoustic phonons. Conversely, in a QW, an exciton-polariton can disappear by giving its energy to a photon emitted in a perpendicular direction to the QW plane. The polariton effect (also sometimes referred to as a retardation effect) consists in this case of the possibility for the emitted photon to be reabsorbed once again by the same exciton. The chain of virtual emission-absorption leads to a finite value of τ and is also responsible for the renormalization of the exciton frequency (3.18). The renormalization does not exceed a few µeV in realistic QWs, while it becomes more important in quantum dots. The radiative lifetime τ is about 10 ps in typical GaAs-based QWs. Though it is extremely hard to observe free excitons in the photoluminescence governed mainly by excitons localized at imperfections of a QW, the lifetime τ of a free exciton of 12 ps has been experimentally measured by Deveaud et al Reference Deveaud, Clérot, Roy, Satzke, Sermage and Katzer[25] on a record quality 100Å-thick GaAs/AlGaAs QW.
3.2 Oblique incidence case
If light is incident on a QW at oblique angle, Equation (3.3) takes a more complex form. Here we examine reflection and transmission of linearly polarized light for TE-polarization (electric field of the light wave in the QW plane, also called s-polarization) and TM-polarization (magnetic field of the light wave in the QW plane, also called p-polarization). Any light-wave having a different polarization can be represented as a linear combination of TE- and TM-polarized waves. In the rest of this section we follow Ref. Reference Ivchenko, Kaliteevski, Kavokin and Nesvizhskii[26].
Thus, in s-polarization, reflection and transmission coefficients are given by:
where
In p-polarization, reflection and transmission coefficients have a more complex form:
where

the parameter Γx,z is proportional to the oscillator strength for excitons polarized parallel and normal to the interface, and Δω0 is the splitting between these states. As follows from interband selection rules, Γz = 0 for e1-hh1 excitons, whereas for the e1-lh1 state both Γz and Γx are nonzero: Γz ≈ 4 Γx (here e, hh, and lh denote the terms electron, heavy hole, and light hole, respectively). Therefore two poles separated by an angle-dependent value of Δω0 are present in the expression for the p-polarized reflection or transmission coefficient near the light-hole exciton resonance. The allowance for the second pole is important for sufficiently large values of φ.
4 Reflectivity of Bragg mirrors
4.1 Normal incidence case
A Bragg mirror is a periodical structure composed of pairs of layers of dielectric or semiconductor materials characterized by different refractive indices (say; n a and n b). The thicknesses of the layers (a and b, respectively) are chosen so that
Condition ((4.1)) is usually called Bragg interference condition. The wavelength of light
At normal incidence, the transfer matrices across the layers which compose the mirror are (see Appendix for details):

where
An infinite Bragg mirror represents the simplest one-dimensional photonic crystal. Its band structure is given by the equation
where T ij are matrix elements of
At the central frequency of the stop-band, given by
the matrix

Its eigen values are:
The reflection coefficient of a semi-infinite Bragg mirror at
which readily yields r=1.
In the vicinity of
The matrix reads, in this approximation,

Equation (4.8) yields in this case

where
The coefficient
is frequently called effective length of a Bragg mirror. Note that it has nothing in common with the penetration length

Figure 4 shows the profile of an electric field of a light wave propagating in a Bragg mirror at the center of the stop-band. Decay of the field is dependent on the contrast between refractive indices nA and nB : the higher the contrast, the faster the decay.

Figure 4. Electric field of a light-wave penetrating into a typical Bragg mirror. Refractive indices of its quarter-wave layers are n A =1.6, n B =2.6.
For a finite-size mirror, the reflection coefficient within the stop-band is different from unity because of the tunneling of light across the mirror. It can be found from the matrix equation:
where

As follows from these formulae, the higher the contrast between nA and nB , the better the reflectivity of the mirror. In many cases we shall approximate the reflection coefficient of the mirror in the vicinity of
Note that, strictly speaking, this approximation is valid only if light propagates normal to the surface of the mirror. Oblique incidence of light on a Bragg mirror will be considered later in this section.
One more important characteristic of a Bragg mirror is the width of its stop-band. It can be found from Equation (4.4). Boundaries of the first stop-band are given by a condition:
Keeping only terms up to the second order in x one can transform this equation:
The splitting between the two solutions is proportional to the stop-band width (in frequency):
The stop-band width increases with increase of the contrast of two refractive indices. Note, that Equation (4.20) is valid only if
which is usually the case in realistic structures. Otherwise, one should solve Equation (4.18) numerically.
4.2 Oblique incidence case
Under oblique incidence the optical thickness of layers composing Bragg mirrors changes. The phase gained by light crossing a layer of thickness a under an angle θA is given by
where nA is the refractive index of this layer. It is evident that the frequency which fulfills the Bragg interference condition ϕ = π/2 is higher for oblique angles than for a normal angle. That is why, at oblique angles, stop-bands of any Bragg mirror shift towards higher frequencies. Also bearing in mind that at oblique angles condition ((4.22)) is satisfied at different frequencies for layers with different refractive indices, one can conveniently define the center of the stop-band as a frequency
where θ0 is the incidence angle, θA,B are propagation angles in layers having refractive indices nA , nB , respectively. They are linked by Snell-Descartes law:
Transfer matrices ((4.2)) are modified in case of oblique incidence. For s-polarized light, one should multiply all the refractive indices by cosines of propagation angles in corresponding media:
For p-polarized light the same replacement should be done in the arguments of the trigonometric functions in ((4.2)), while in the coefficients one should substitute:
Condition ((4.8)) still holds at oblique incidence. It provides the expression for frequency dependent phase of the reflection coefficient
Thus, reflection coefficient rB of a Bragg mirror at oblique incidence near the center of the stop-band is given by Equation (4.17), where the amplitude is the same as for normal incidence (Equation (4.16)), while the phase is changed according to Equation (4.27) and Equation (4.23).
Note that for finite Bragg mirrors at very big incidence angles, the amplitude of rB is also affected. It decreases with increase of θ0 faster in p-polarization than in s-polarization. Later on, we will neglect this effect.
5 Dispersion of exciton-polaritons in the microcavities containing a single quantum well
Consider a symmetric microcavity having a single QW embedded in the middle. In the basis of amplitudes of light-waves propagating in positive and negative direction along z-axis, the transfer matrix across the QW has a form (see Appendix for details):
where rQW and tQW are angle and polarization dependent amplitude reflection and transmission coefficients of the QW derived in Equation (3.14).
The transfer matrix across the cavity from one Bragg mirror to another one is a product:
where Lc is the cavity width.
The elements of this matrix are:
To find eigen-frequencies of exciton-polariton modes of the microcavity one should look for nontrivial solutions of Maxwell equations under the requirement of no light incident on the cavity from the outside. This yields
where rB is the angle-dependent reflection coefficient of Bragg mirrors for light incident from inside the cavity introduced in Equation (4.17). Excluding the coefficient A from Equation (5.4), we obtain the following equation for polariton eigen-modes
This is already a dispersion equation because the coefficients of the transfer matrix and rB are dependent on the in-plane wave-vector of light. Substituting coefficients (5.3) into (5.5) one can represent the dispersion equation in the following form:

Solutions of Equation (5.6) coming from roots of the second paranthesis in its left part coincide with pure odd optical modes of the cavity. These modes have a node in the center of the cavity where a QW is situated. Therefore, they are not coupled with the ground exciton state having an even wave-function. The first paranthesis of the left part of (5.6) contains the reflection coefficient of the QW which is dependent on excitonic parameters. Roots of this paranthesis describe eigen-states of exciton-polaritons resulting from coupling of even optical modes with the exciton ground state. Further in the text we will consider only these states. We neglect here and later excited exciton states that may be coupled to odd cavity modes.
For the even modes and normal incidence, if we take
we obtain
where

This is an equation for eigen-states of a system of two coupled harmonic oscillators, namely, the exciton resonance and the cavity mode. Note, that in this form Equation (5.8) has been published for the first time by Savona et al Reference Savona, Andreani, Schwendimann and Quattropani[27], while its general form Equation (5.5) has been obtained in Reference Kavokin and Kaliteevski[28]. Equation (5.8) is only applicable in the normal incidence case. Thus, in order to calculate dispersion relations of the exciton-polaritons in microcavities, one should, in principle, use Equation (5.5). On the other hand, in most cases it suffices to take into account the wave-vector dependence of resonance frequencies ωc and ω0 to obtain a reasonable approximation to the true dispersion curves.
The parameter V is the strength of coupling between the cavity photon mode and the exciton resonance. If
anticrossing takes place between exciton and photon modes and is characteristic of the strong coupling regime. In this regime, two distinct exciton-polariton branches manifest themselves as two optical resonances in reflection of transmission spectra. The splitting between these two resonances is referred to as vacuum field Rabi splitting. It achieves 4-15 meV in existing GaAs-based microcavities, up to 30 meV in CdTe-based microcavities, and is expected to be as large as 50 meV in future GaN cavities. The advantage of GaN is that A and B excitons in this semiconductor have a record oscillator strength, exceeding by an order of magnitude the oscillator strength in GaAs Reference Julier, Campo, Gil, Lascaray and Nakamura[29].
If
the weak-coupling regime holds, characterized by crossing of the exciton and photon mode and increase of the exciton decay rate at the resonance point. This regime is typically used in vertical cavity surface emitting lasers (VCSELs). Note that all the above theory neglects the disorder effect on the exciton resonance. Taking into account inevitable inhomogeneous broadening of the exciton resonance and Rayleigh scattering of exciton-polaritons one should also modify the criterion ((5.9)) for weak-coupling-strong-coupling threshold Reference Whittaker[16]. This is out of the scope of this article.
Dispersion of exciton-polaritons in microcavities has a purely classical nature. However, polaritons themselves can be considered as quantum quasi-particles. This consideration makes sense when their relaxation along the dispersion curves is discussed. Relaxation of polaritons is considered in the next section.
6 Polariton Bose-condensation and superfluidity in microcavities
An exciton is a Coulomb-correlated electron-hole pair. It is a neutral particle of integer spin value. Depending on their density and on temperature, excitons can behave as a weakly interacting Bose gas, a metallic liquid, or an electron-hole plasma. It has been understood by Moskalenko Reference Moskalenko[30] and Blatt Reference Blatt, Boer and Brandt[31] that excitons remain in the gas phase at low densities and low temperatures and are therefore good candidates for observation of Bose-Einstein condensation (BEC). A great research effort has been dedicated to the problem of exciton Bose condensation. A number of theoretical works on excitonic condensation and superfluidity has appeared Reference Keldysh and Kozlov[32] Reference Haug and Hanamura[33] Reference Comte and Nozières[34] Reference Lozovik and Yudson[35] Reference Lozovik and Yudson[36] Reference Lozovik and Yudson[37]. In most of these works, the fermionic nature of excitons is addressed as well. The starting point of these models is a system of degenerate electrons and holes of arbitrary densities which are treated in the spirit of the BCS theory. A key point of all the formalisms developed is that they assume infinite lifetime of the semiconductor excitations. In other words these theories are looking for steady state solutions of a Schrödinger equation of interacting excitons. It is indeed clear that to have enough time to Bose-condense, excitons must have a radiative lifetime much longer than their relaxation time. Thus the use of “dark” (uncoupled to light) excitons seems preferential. This is the case of bulk Cu2O paraexcitons whose ground state spin is 2 or of excitons in coupled quantum wells Reference Keldysh and Kozlov[32] Reference Lozovik and Yudson[35] Reference Lozovik and Yudson[36] Reference Lozovik and Yudson[37] where the electron and hole are spatially separated. These two systems have been subjected to energetic experimental studies which have sometimes claimed achievement of exciton BEC or superfluidity Reference Griffin, Snoke and Stringari[38] Reference Snoke, Denev, Liu, Pfeiffer and West[39] Reference Lozovik and Ovchinnikov[40] Reference Butov, Lai, Ivanov, Gossard and Chemla[41] Reference Butov, Ivanov, Imamoglu, Littlewood, Shashkin, Dolgopolov, Campman and Gossard[42]. However, a careful analysis by Lozovik and Tikhodeev Reference Lozovik and Ovchinnikov[40] Reference Tikhodeev[43] showed that a clear evidence of excitonic BEC has not yet been achieved. The difficulties to Bose-condense excitons are twofold. The first reason is the intrinsic imperfections of semiconductors. Because of an unavoidable structural disorder, dark excitons non-resonantly excited are often trapped in local minima of the disorder potential and can hardly be considered as free bosons able to condense. The second source of difficulties is connected with a problem of detection of the condensed phase. The clearest signature of exciton Bose condensation should be the emission of a coherent light by spontaneous recombination of condensed excitons Reference Lozovik and Ovchinnikov[40]. Such emission is a prioriforbidden for a system of dark excitons.
On the other hand, “bright” excitons directly coupled to light might also be good candidates for condensation despite their short lifetimes. In bulk semiconductors this coherent coupling gives rise to a polarization wave that can be considered from a quantum mechanical point of view as a coherent superposition of pure excitons and photon states Reference Hopfield[6] Reference Agranovich[7]. A quasiparticle state resulting from this superposition is referred to as an exciton-polariton (polariton). Bulk polaritons are stationary states that transform into photons only at surfaces. Polaritons are bosons and can, in principle, form condensates that would emit spontaneously coherent light. This process will be referred to in the course of this article as polariton lasing .
Typical dispersion curves of bulk polaritons are shown in figure 5. The steps needed to achieve polariton lasing in this system are as follows. Initially, optically or electronically excited electrons and holes form excitons. Excitons thermalize at their own temperature through exciton-exciton interaction. They reduce their kinetic energy interacting with phonons and relax along the lower polariton branch (figure 5). In the vicinity of the exciton-photon intersection point, the density of states of polaritons is strongly reduced and the excitonic contribution to the polariton is decreased. One should note that strictly speaking, a k=0 photon does not exist and that consequently, k= 0 polaritonic state of the lower polariton branch does not exist either. The polariton dispersion has no minimum so that a true condensation process is strictly forbidden. Polaritons accumulate in a large number of states in the so-called bottleneck region.

Figure 5. Dashed line : Dispersion relation of uncoupled photons and excitons in a semi-infinite semiconductor. Solid line : Dispersion relation of bulk exciton-polaritons in the regime of strong exciton-light coupling. One can see that there is no lower branch ground state.
The situation is drastically different in microcavities, where a semiconductor layer (generally a quantum well) is embedded in an optical cavity (Fabry-Perot resonator). The cavity prevents the escape of photons and allows the formation of long lifetime cavity polaritons Reference Weisbuch, Nishioka, Ishikawa and Arakawa[1]. The in-plane cavity polariton dispersion is shown in figure 6-a. One can see that contrary to the bulk case the dispersion exhibits a well defined minimum located at k=0 (k being the in-plane polariton wave vector). This makes cavity polaritons good candidates for BEC. They have moreover an extremely small effective mass around k=0 which provides a large critical temperature for condensation. Experimental discovery of stimulated scattering of exciton-polaritons in semiconductor microcavities containing QWs by Savvidis and Baumberg Reference Savvidis, Baumberg, Stevenson, Skolnick, Whittaker and Roberts[5] has proved that a microcavity is probably the most suitable system to evidence effects linked to the bosonic nature of exciton-polaritons. On the other hand, polaritons are 2D quasi-particles that cannot exhibit a strict BEC phase transition Reference Mermin and Wagner[44] Reference Hohenberg[45] Reference Coleman[46], but rather a local condensation or a Kosterlitz-Thouless phase transition Reference Kosterlitz and Thouless[47] Reference Fisher and Hohenberg[48] Reference Lozovik, Bergmann and Panfinov[49] Reference Koinov[50]. A fundamental peculiarity of the system is also a strongly non-equilibrium population of polaritons because of their finite lifetime. The relaxation kinetic of polaritons plays a major role in this case.

Figure 6. a) Dashed line : Dispersion relation of uncoupled photons and excitons in a GaAs microcavity. Solid line : Dispersion relation of microcavity polaritons in the strong-coupling regime in a typical GaAs-based cavity. b) Dispersion relation of polaritons in a model GaN-based microcavity. The arrows sketch exciton relaxation paths trough their interaction with acoustic phonon and their blocking in the bottleneck region. c) Scheme of the experiment performed in Reference Savvidis, Baumberg, Stevenson, Skolnick, Whittaker and Roberts[5]. A short pumping laser pulse creates a polariton population at the inflexion point of the lower polariton branch dispersion. A probe pulse illuminates the cavity under normal incidence within a short delay with respect to the pump. It seeds the ground polariton state, stimulating the resonant polariton-polariton scattering.
7 Statistical properties of cavity polaritons
Consider a typical microcavity structure Reference Skolnick[51]. The optical cavity having a refractive index n quantizes the light wave vector in the growth direction, so that it can only be equal to π/(nLz) or to any integer multiple of this quantity. The in-plane polariton propagation remains free. The cavity photon dispersion thus reads (see figure 6-a):

This dispersion is quasi-parabolic for small wave vectors and is characterized by a photon effective mass:
Contrary to the three dimensional case, photons interact with the cavity mirrors and have consequently a mass which is typically 105 times smaller than the free electron mass. As one can see in figure 6-a, cavity polariton dispersion is strongly non-parabolic, especially for the lower polariton branch that can be separated in two distinct zones. The smaller central zone where the polariton wave vector is less than the light wave vector in bulk crystal contains a deep and sharp minimum, where the polariton mass is close to the cavity photon mass. The remaining of the lower branch is completely exciton-like.
Imamoglu Reference Imamoglu, Ram, Pau and Yamamoto[18] Reference Imamoglu and Ram[19] was first to propose the use of the bosonic character of cavity polaritons to build up an exciton-polariton condensate subsequently emitting a coherent laser light by spontaneous emission. His idea was to create an equilibrium (non thermal!) polariton distribution by external optical pumping. The relaxation of this non-thermal distribution through its interaction with acoustic phonons was assumed to be able to provide an efficient polariton accumulation in their ground state. However, a number of peculiarities of cavity polaritons, especially their unusual dispersion shape, has not been taken into account in the proposed model, which therefore missed most of the physics of real microcavities. It has indeed been demonstrated, one year later by Tassone Reference Tassone, Piermarocchi, Savona, Quattropani and Schwendimann[52], that acoustic phonons cannot provide an efficient polariton relaxation towards the ground state because of the steep central part of the polariton dispersion “bottleneck region” where its slope exceeds the sound velocity (figure 6-b). Nevertheless, a quadratic dependence of emission on the non-resonant pumping power has been evidenced experimentally in II-VI Reference Dang, Heger, Andre, Boeuf and Romestain[53] and III-V Reference Senellart and Bloch[54] Reference Senellart, Bloch, Sermage and Marzin[55] microcavities. This was a proof that other relaxation mechanisms allow a part of polaritons to cross the bottleneck region. The main of these additional mechanisms is the exciton-exciton scattering Reference Tassone and Yamamoto[56]. F. Boeuf et al., Reference Boeuf, André, Romestain, Dang, Péronne, Lampin, Hulin and Alexandrou[57] Reference Alexandrou, Bianchi, Péronne, Hallé, Boeuf, André, Romestain and Dang[58] have reported exponentially growing emission intensity versus pumping intensity and have claimed that bosonic stimulation of relaxation to the ground state takes place in their experiments. However neither the ground state occupation factor nor the coherence of the emitted light have been checked in these works and it seems to us that no clear evidence of polariton lasing has there been given.
A real breakthrough came from an experiment performed under resonant excitation by Savvidis and Baumberg Reference Savvidis, Baumberg, Stevenson, Skolnick, Whittaker and Roberts[5]. They have macroscopically populated the inflection point of the lower polariton branch (wave vector k0 ) by a 1 ps pump pulse (see figure 6-c). A weak probe pulse sent at a normal angle to the sample within a short delay was used to seed the polariton ground state. This stimulated a simultaneous scattering of one k0 polariton to the ground state and another one to the state 2k0 . This stimulated process, conserving the energy and the wave-vector, provided an amplification of the probe reflection by a factor of 70. Similar results have been obtained under cw excitation by Stevenson and Skolnick in GaAs-based cavities Reference Stevenson, Astratov, Skolnick, Whittaker, Emam-Ismail, Tartakovskii, Savvidis, Baumberg and Roberts[59] and by Saba et al in CdTe based structures Reference Saba, Ciuti, Bloch, Thierry-Mieg, Adré, Dang, Kundermann, Mura, Bongiovanni, Staehli and Deveaud[60]. In this latter case, stimulated scattering to the ground state was seen up to 200 K. Strong dressing of the dispersion relation due to the interaction between coherently populated states has also been observed Reference Savvidis, Ciuti, Baumberg, Whittaker, Skolnick and Roberts[61] and successfully interpreted by Ciuti Reference Savvidis, Ciuti, Baumberg, Whittaker, Skolnick and Roberts[61] by a generalisation of the Bogoliubov Reference Bogoliubov and Phys[62] Reference Zagrebnov and Bru[63] approach. These experimental results have clearly demonstrated the bosonic behaviour of cavity polaritons up to quite high pumping intensities and temperatures. Complex spin dynamics, a signature of strong bosonic effects, has also been observed under resonant excitation by Lagoudakis et al Reference Lagoudakis, Savvidis, Baumberg, Whittaker, Eastham, Skolnick and Roberts[64] and recently under non resonant excitation by Martin et al. Reference Martin, Aichmayr, Viña and André[65]. These last results are not yet fully understood Reference Kavokin[66], but reveal the possibilities associated with this new research area. Finally, very recently an increase of coherence of light emitted from a ground polariton state in a GaAs-based microcavity containing 12 QWs versus non-resonant pumping intensity has been reported Reference Deng, Weihs, Santori, Bloch and Yamamoto[21]. This extremely promising result still needs to be carefully understood. An important point is whether the coherence of emission is due to polariton Bose-condensation or if it is just endowed by the coherence of the pumping laser light. This discovery could represent a step towards the achievement of a quasi-Bose condensation effect in solid state systems.
The most challenging objective for this active field is now without any doubt to clearly achieve polariton coherence in non-resonantly pumped microcavities. The buildup of a ground state coherent population can be interpreted as a phase transition towards a Bose condensed state or as “polariton lasing” effect resulting from bosonic stimulated scattering. A criterion for Bose condensation in a macroscopic ground state density in the thermodynamic limit is:
where N 0 is the ground state population and R the system size. On the other hand, the bosonic stimulated scattering is not necessarily an equilibrium property and the criterion is less restrictive:
Both BEC and stimulated scattering effects are based on the same physics, namely on a trend of bosons to accumulate in the same (ground) quantum state. Actually, stimulated scattering represents a dynamical aspect of Bose-condensation.
“Polariton lasers” exploit both of these effects. Formation of the condensate within the polariton lifetime is only possible because of the rapidity of stimulated scattering. Once condensed, polaritons emit coherent monochromatic light. Here and further by “emission of light by polaritons” we mean escape of light from the cavity by its tunneling through the Bragg mirrors. As the light emission by a polariton quasi-condensate is spontaneous, there is no population inversion condition required in polariton lasers, absorption of light does not play any role, and ideally there is no threshold for lasing. Concerning this latter point, the argument is that it is sufficient to have two polaritons in the ground state for creating a condensate and thereby collecting two coherent photons.
A few theoretical works attempting to describe these phenomena have appeared recently. An analysis based on the Dike model has been proposed by Eastham and Littlewood Reference Eastham and Littlewood[67] to describe the 0 K properties of an arbitrary pumped microcavity including disorder and space filling effect. Malpuech et al. have defined a simple criterion for polariton quasi-condensation in finite size 2D system and have plotted the corresponding polariton phase diagram Reference Malpuech, Di Carlo, Kavokin, Baumberg, Zamfirescu and Lugli[68]. This paper shows that room temperature polariton lasing was achievable in hypothetic microcavities based on large band gap semiconductors Reference Malpuech, Di Carlo, Kavokin, Baumberg, Zamfirescu and Lugli[68] Reference Zamfirescu, Kavokin, Gil, Malpuech and Kaliteevski[69]. Kinetic aspects of polariton relaxation have also been studied, mainly by numerical solution of semi-classical Boltzmann equations. Malpuech et al have proposed to introduce a free electron gas in the cavity in order to speed up the polariton relaxation Reference Malpuech, Kavokin, Di Carlo and Baumberg[70]. Soroko and Ivanov Reference Soroko and Ivanov[71] have proposed to use microcavities at very positive detuning in order to suppress the relaxation bottleneck, keeping advantage in this geometry of a polariton mass still smaller than the exciton one. This idea is however achievable only in extremely high quality structures, probably far beyond the actual growth abilities. Finally, Porras et al. have presented a simulation Reference Porras, Ciuti, Baumberg and Tejedor[72] demonstrating that existing II-VI microcavities might exhibit polariton lasing at low temperatures and achieved a qualitative agreement with experimental results.
8 Cavity polariton phase transition
8.1 Kosterlitz Thouless phase transition
In this chapter, we discuss thermodynamic properties of microcavities polaritons considered as equilibrium particles, i.e., particles having an infinite lifetime. Even though this approximation is very far from reality, mainly governed by relaxation kinetics, it is definitely instructive to examine the BEC conditions in this limiting case. We will moreover assume that polaritons behave as either ideal or weakly interacting bosons so that the following analysis is valid only in a weak density limit.
Let us start with the Bose-Einstein distribution function:

where μ is the chemical potential,
where d is the dimensionality of the system. The critical concentration of bosons needed for condensation is given by
The critical density is finite for a non-zero temperature if d > 2. However, the integral ((8.3)) diverges in the 2D case. Thus, a non-interacting Bose gas cannot condense in an infinite two-dimensional system and the same statement turns out to be true when interactions are taken into account. A rigorous proof of the absence of BEC in 2D has been given by Hohenberg Reference Hohenberg[45]. And equivalent statement known as the Mermin-Wagner theorem assert that long range order cannot exist in system of dimensionality lower than 2 Reference Mermin and Wagner[44]. Finally, it has been shown that spontaneous symmetry breaking does not occur in 2D Reference Coleman[46]. However a phase transition between a normal state and a superfluid state can take place in 2D as it has been predicted by Kosterlitz and Thouless 30 years ago Reference Kosterlitz and Thouless[47] in the framework of the XY model. Such first order phase transition is forbidden for ideal bosons, but it can take place in systems of weakly interacting bosons Reference Fisher and Hohenberg[48] like low density excitons Reference Lozovik, Bergmann and Panfinov[49] Reference Koinov[50] or polaritons. We are now going to describe qualitatively how this phase transition takes place and what are the differences with a true BEC effect. At temperatures higher than the critical temperature TKT , the superfluid density ns is zero, but local condensation can take place. Condensate droplets can have quite large sizes as we will see later, however the correlation function of the quasi-condensate wavefunction is decreasing exponentially and the droplets are not connected together. Defects, or votices, prevent long range ordering, i.e., connection of the quasi-condensate droplets. However, once the critical temperature TKT is reached, single vortices are no more stable: they bind, forming pairs and clusters, allowing a sudden connection between quasi-condensate droplets so that a superfluid is formed whose density is Reference Nelson and Kosterlitz[73]:
where m is the ground state mass. Superfluidity means that two points on the surface are statistically connected by a phase coherent path. Defects (vortices) remain as well below TKT , which means that the superfluid does not homogeneously fill the space. The correlation function is not constant but decreases as a power law. The superfluid wave function has thus a finite extension in reciprocal space and is consequently not a BEC wave function. A complete homogeneity can be achieved only at T=0 where vortices disappear. Below TKT normal and superfluid phases coexist. The normal fluid can be characterized by a density nn and a velocity
whereas the normal fluid density is given by the Landau formula Reference Khalatnikov[74]:
where m(k) is the wave vector dependent polariton mass, fB isthe Bose distribution function ((8.5)) and Ebo is the Bogoliubov dispersion relation valid for interacting bosons, to which are associated new quasi-particles (the so-called bogolons) Reference Bogoliubov and Phys[62] Reference Zagrebnov and Bru[63]:
µ is the polariton chemical potential given in our case by:
with V(k) the Fourier transform of boson-boson potential of interaction given by V(k) = 6×(k)Ebab 2 , where x is the exciton fraction in the polariton wave-function, Eb is the exciton binding energy, and ab is the two dimensional exciton Bohr radius. Equations (8.6-8.8) yield ns(T,n). Its substitution into Equation (8.8) allows to obtain TKT(n). As one can see from Equation (8.7), repulsive particle interaction makes the bogolons Reference Bogoliubov and Phys[62] Reference Zagrebnov and Bru[63] dispersion relation linear around k=0. Hence elementary excitations from the ground state are sound-like and dissipation-less. They are therefore responsible for the superfluid properties of the 2D gas.
Solid lines on Figure 7 (a,b,c,d) show the critical concentration for the KT phase transition according to the abovementioned procedure and calculated for typical microcavity structures based on GaAs (a), CdTe (b), GaN (c), and ZnO (d). In all cases, we assume zero detuning of the exciton resonance and the cavity photon mode. For GaAs- and CdTe-based microcavities we have used the parameters of experimentally studied samples reported in Refs. Reference Dang, Heger, Andre, Boeuf and Romestain[53] Reference Tassone, Piermarocchi, Savona, Quattropani and Schwendimann[52]. Parameters of model GaN and ZnO microcavity structures can be found in Refs. Reference Malpuech, Di Carlo, Kavokin, Baumberg, Zamfirescu and Lugli[68] Reference Zamfirescu, Kavokin, Gil, Malpuech and Kaliteevski[69]. The two latter structures have for now only a hypothetic interest, since the strong coupling is not yet achieved experimentally in GaN and ZnO based cavities. Vertical and horizontal dashed lines in Figure 7 show the approximate limits of the strong coupling regime in the microcavity that come from either exciton screening by photo-induced electron-hole plasma or from temperature-induced broadening of the exciton resonance.

Figure 7. Phase diagrams for GaAs (a), CdTe (b), GaN (c), and ZnO (d) based microcavities.
Vertical and horizontal dashed lines show the limits of the strong-coupling regime imposed by the exciton thermal broadening and screening, respectively. Solid lines show the critical concentration N c versus temperature of the polariton KT phase transition. Dotted and dashed lines show the critical concentration N c for quasi condensation in 100 µm and 1 meter lateral size systems, respectively. The thin dotted line symbolizes the limit between vertical cavity surface emitting laser (VCSEL) and light-emitting diode regimes.
Note that the limiting concentration of polaritons in a microcavity is imposed by the strong-weak coupling threshold rather than by the Mott transition Reference Khitrova, Gibbs, Jahnke, Kira and Koch[75]. This threshold takes place because of the decrease of the exciton oscillator strength caused by a bleaching effect. The weakly interacting boson model we have presented is therefore perfectly valid in the strong coupling regime. Above the critical density, if still in the strong coupling regime, a microcavity operates as a polariton diode emitting an incoherent light, while in the weak coupling regime the device behaves like a conventional light-emitting diode. Above the critical density, in the weak coupling regime, the microcavity acts as a conventional laser. Thin dotted lines in figure 7 indicate the limit between two latter phases that can not be found in the framework of our formalism limited to the strong coupling regime. One can note that critical temperatures achieved are much larger than those that can be achieved in exciton systems. In existing GaAs and CdTe-based cavities these temperatures are high enough for experimental observation of KT-phase transition in laboratory conditions, but do not allow the production of devices working at room temperature. Record critical temperatures of TKT=400 K and 560 K for GaN- and ZnO-based model cavities are given by extremely high exciton dissociation energies in these semiconductors. It is interesting to note that even above TKT(n), n − nn does not vanish, which reflects the existence of isolated quasi-condensate droplets. As we show below, these droplets can reach substantial size, even above Kosterlitz-Thouless temperature or density. Their properties could dominate the behaviour of real systems as we will discuss in the next sub-section.
8.2 Quasi-condensation and local effects
In this section we define a rigorous criterion for boson quasi-condensation in finite size systems. For the sake of simplicity we neglect here all kinds of interactions between bosons. Let us consider a system of size R. The particle density is given by
where N0 is the ground state population. We define the critical density as the maximum number of bosons that can be accommodated in all the states except the ground state:
The quasi condensate density is thus given by n0 = n - nc . In this case, formally, the chemical potential μ is always strictly negative, but it approaches zero allowing to put as many bosons as we want in the ground state while keeping concentration of bosons in all other states finite and limited by n c. Concentration (8.10) can be considered as the critical concentration for local quasi-Bose condensation in 2D-systems. Later, we shall refer to T c defined in this way as the critical temperature of Bose condensation in a finite 2D-system. On the other hand it appears possible, knowing temperature and density, to deduce typical coherent droplet size which is given by the correlation length of the quasi-condensate.
From a practical point of view, experiments are performed on samples having a lateral size of about 1 cm. Electron-hole pairs are generated by a laser light having a spot area of about 100 µm. These electron-hole pairs rapidly (typically on a time-scale less than 1 ps) form excitons that relax down to the optically active region where they strongly interact with the light field to form polaritons. The excitons that form polaritons have a finite spatial extension in the plane of the structure, but they are all coupled to each other via light Reference Mapuech and Kavokin[76] Reference Kavokin, Malpuech and Langbein[77]. The polariton system thus covers the whole surface where excitons are generated. If KT critical conditions are not fulfilled, but if typical droplets size are larger than the light spot size, the whole polariton system can be transiently phase coherent and thus exhibits local BEC. As we will show below, this situation is the most likely to happen in current optical experiments performed at low temperature.
Let us underline at this point an important advantage of polaritons with respect to excitons weakly coupled to light for the purposes of BEC or superfluidity. Actually, individual excitons in real structures are subject to strong localisations in inevitable potential fluctuations that prevent them from interacting and forming condensed droplets. Polaritons are basically delocalized even though the excitons forming them could be localized. That is why their interactions are expected to be more efficient and bosonic behaviour more pronounced.
Dotted and dashed lines on Figure 7 (a,b,c,d) show the critical concentration for local quasi condensation in microcavity systems having 100 µm and 1 meter lateral sizes, respectively. In the high-temperature (high-concentration) limit, critical concentrations are very similar for both lateral sizes and they slightly exceed critical concentrations of the KT phase transition. This means that in this limit the KT transition takes place before droplets size achieve 100 µm. Conversely, in the low-temperature (low concentration) limit, the KT curve is between the transition curves of the 100 µm and 1 meter size systems. This shows that droplets at the KT transition are larger than 100 µm but smaller than 1 m. Since the typical laser spot size is of about 100 µm, this means that local Bose condensation takes place before KT transition at low pumping. A detailed analysis could allow to obtain the percolating droplets size versus temperature, which is out of our present scope.
9 Polariton lasing
Microcavity polaritons have finite lifetime, ranging from 1-2 ps to about 1000 ps depending on their in-plane wave-vector. This is why non-resonantly excited polaritons may have no time to relax to their equilibrium distribution ((8.5)). If their relaxation time is shorter than the lifetime, they emit light in a wide energy and wave-vector range instead of yielding a strong coherent emission signal from k=0 state. Actually, in most microcavity samples studied so far the polariton relaxation time is much longer than the lifetime and the emission remains broad. The origin of such a slow relaxation dynamics is a kinetic blocking effect also called bottleneck effect. The bottleneck region of the lower polariton branch corresponds to the transition from the exciton-like to the photon-like dispersion (see figure 6-b). While relaxation with acoustic phonons along the excitonic part of the dispersion curve is very quick, the acoustic-phonon assisted scattering in the photonic part of the dispersion requires high-energy acoustic phonons whose density is close to zero at low temperatures as pointed out by Tassone Reference Tassone, Piermarocchi, Savona, Quattropani and Schwendimann[52]. Thus, most of photoluminescence comes from the bottleneck region, and the population of the k=0 state remains much lower than what one could expect from the equilibrium distribution function Reference Boeuf, André, Romestain, Dang, Péronne, Lampin, Hulin and Alexandrou[57] Reference Stevenson, Astratov, Skolnick, Whittaker, Emam-Ismail, Tartakovskii, Savvidis, Baumberg and Roberts[59] Reference Butté[78] Reference Alexandrou, Bianchi, Péronne, Hallé, Boeuf, André, Romestain and Dang[58] Reference Tartakovskii[79] Reference Tartakovskii[80].
We see two possible ways to suppress the bottleneck effect and to achieve polariton lasing. First, in the future GaN or ZnO-based cavities, at room temperature if the strong coupling regime still holds, acoustic phonon relaxation should be much more efficient than in presently available cavities at Helium temperature. Second, n-doping of microcavities is expected to allow efficient electron-polariton scattering within the photon-like part of the dispersion Reference Malpuech, Kavokin, Di Carlo and Baumberg[70]. Here we present the formalism based on solving numerically the semi-classical Boltzmann equation Reference Uehling and Uhlenbeck[81] for polaritons that illustrates the above statements.
We simulate relaxation of cavity polaritons excited non-resonantly in a continuous regime. A Boltzmann equation is solved numerically in two-dimensional reciprocal space:

where nk is the polariton distribution function in the state having a wave vector k, Pk is the generation term describing optical pumping. Γk is the recombination rate composed of both radiative and nonradiative components. W k→k′ is the total scattering rate between the states k and k'. This scattering rate is composed of three terms in our model, namely: polariton-acoustic phonon scattering (rate Wa ), polariton-polariton scattering (rate Wx ), and polariton-electron scattering (rate We ). We assume perfect cylindrical symmetry for the polariton distribution function, implying that the population of a state k is only a function of the absolute value of the wave-vector, relevant to the case of nonresonant pumping. Only the intrabranch scattering within the lower polariton branch is considered. We calculate the radiative recombination rate, polariton-acoustic phonon, and the polariton-polariton scattering rates as Tassone Reference Tassone and Yamamoto[56]. The polariton-electron scattering rate is calculated using the Fermi golden rule as in our paper Reference Zamfirescu, Kavokin, Gil, Malpuech and Kaliteevski[69]. Boltzmann equations are in principle written for an infinite system and describe distribution function evolution versus time. Strictly speaking one cannot demonstrate true condensation effect but rather stimulated scattering and lasing. Such equations cannot however describe the buildup of phase coherent polariton field. A formalism describing the time evolution of this phase has been developed by Banyai Reference Zagrebnov and Bru[63] but it includes only interactions with phonons. A more general formalism, making the link between Boltzmann equation and phase coherent polariton field, including all kinds of interactions, has been recently developed by Laussy et al Reference Laussy[82], but is still unpublished.
Figure 8 shows the equilibrium distribution function under continuous pumping for a GaAs-based microcavity having a normal-mode splitting of 5 meV containing a single QW, and for zero detuning of cavity and exciton modes. All the cavity parameters were taken from the work by Tassone Reference Tassone and Yamamoto[56]. We have assumed cavity photon lifetime of 8 ps, and exciton radiative lifetime of 20 ps. The polariton nonradiative lifetime is chosen constant over the whole reciprocal space (1 ns). For all the curves the pump power absorbed by the single QW is set to be 4.2 W/cm2 between k=3×106 cm−1 and k=5×106 cm−1 roughly equivalent to an excess of energy of 20 meV. Note that the results we present are not strongly sensitive to the pumping conditions, which allow for both optical and electrical pumping mechanisms.

Figure 8. Distribution function of polaritons at 10 K when non-resonantly pumped with a power of 4.2 W/cm2. Results are shown for (a) polariton-acoustic phonon scattering (dotted), (b) as (a) plus polariton-polariton scattering (dashed) , and (c) as (b) plus polariton-electron scattering (solid). The thin dotted line shows the equilibrium Bose distribution function with zero chemical potential.
Taking into account only the acoustic phonon scattering (curve (a) in Figure 8), a thermal distribution function is seen only beyond k=2×104 cm−1 (the bottleneck region) where polaritons accumulate. Equilibrium is reached after 10 ns leaving a polariton density of 2.5×1010 cm−2. Including both polariton-polariton and polariton-acoustic phonon scattering processes (curve (b) in Figure 8) shows partial relaxation of the bottleneck and a flat polariton distribution. However, the polaritons equilibrium density in the cavity remains the same, close to the saturation density for excitons (about 5×1010 cm−2). The distribution function near the polariton ground state approaches one. This result is in excellent agreement with experimental results obtained recently by Sellenart, Butté and Tartakovskii Reference Senellart, Bloch, Sermage and Marzin[55] Reference Uehling and Uhlenbeck[81], showing that amplification threshold for the distribution function at the trap state is reached when the strong coupling regime is likely to be suppressed. To get an increase in the population of the lowest k state one has to increase the population of a large number of states requiring a large density of excitons. This is due to the flat shape of the distribution function which comes from the nature of the polariton-polariton scattering process (each scattering event increases population of the high-k states. Relaxation of polaritons from these states is then assisted only by phonons and is slow). The radiative efficiency, which we estimate as the ratio of the concentration of photons leaving the cavity within a cone of less than 1° to the pumping intensity, is thus only 1.7%.
When all three scattering processes listed above are taken into account (curve c in Figure 8), a huge occupation number of the lowest energy state of more than 104 is achieved. This system thus acts as a polariton laser in which scattering of polaritons injected at high k by optical or electrical pumping is stimulated by population of low k-states (ground state). In this situation the light power emitted in a cone of 1° is 2.3 W/cm2 and the efficiency of the energy transfer from pump to emitted light is about 80%. The light emitted by the cavity is much more directional and comes from a smaller number of states than in the case (b). The equilibrium polariton density in the cavity is now 1.25×109 cm−2, i.e., 20 times lower than in cases (a,b). Pump powers at least forty times stronger can be used before the strong to weak-coupling threshold is reached. The thin dotted line in Figure 8 shows the equilibrium polariton density from a Bose distribution function (1) plotted for zero chemical potential. It follows quite closely the curve (c) which clearly demonstrates that a thermodynamic equilibrium is practically achieved for this value of the chemical potential, which is a signature of Bose condensation of polaritons. This is confirmed by tracking the temporal evolution of the distribution function at the ground state for different excitation powers (Figure 9a). For the strongest pumping, it is strongly enhanced at very short times as soon as it exceeds one, demonstrating Bose amplification of the final state population. The dashed curve corresponds to the threshold condition for Bose amplification, producing an equilibrium population of the k 0 state slightly exceeding 1, but without significant amplification occuring.
Figure 9(b) shows the temporal evolution of population of the ground state for different degrees of doping in the system. The equilibrium density is strongly enhanced and exceeds the lasing threshold for electron densities above 10×1010 cm−2. Figure 10 shows the radiative efficiency of the device as a function of input power with (a) and without (b) polariton-electron scattering. In the first case, the emission rises quadratically up to the threshold, while in the second case it is much larger and linearly increases. The dotted line on the curve b marks the excitation conditions for which the strong coupling regime collapses because of bleaching of excitons. For the doped microcavity, an excitation area of a 100 μm diameter corresponds to an extremely low threshold power of 3 μW. However, high excitation powers can also be used, while conserving the strong coupling regime.

Figure 9. Polariton occupation of the k=0 state vs time for (a) excitation powers of 0.42 W/cm2 (dashed), 4.2 W/cm2 (dotted), 168 W/cm2 (solid). The pump is turned on at t=0. The corresponding total polariton equilibrium densities are 7.0×1010 cm−2, 1.3×109 cm−2 and 1.3×1010 cm−2. (b) As (a) for a pump power of 0.42 W/cm2 and electron doping of 2.5 × 109 cm−2 (dashed), 1010 (dotted), 4×1010 cm−2 (solid).
Finally, we address the effect on the characteristics of the polariton laser of the heating of the electron gas due to electron-exciton scattering. The dashed line in figure 10 shows the radiative efficiency of the polariton laser calculated while taking into account the dynamics of free electrons. The calculation simultaneously solves the Boltzmann equation for the exciton-polaritons together with the Boltzmann equation for the electron gas. Because of the strong electron-electron interaction, we assume that the electron gas follows a Fermi-Dirac statistics at an electron temperature Te. This equilibrium electron distribution interacts only with polaritons and phonons. One can see that the result is identical to the curve obtained for the equilibrium Fermi-distribution of electrons for pump intensities below 100 W/cm2. This is because of efficient electron-electron scattering (rate about 1.5 ps−1 in our case) which leads to rapid relaxation of the electron gas to its thermal equilibrium. At pump intensities of 1000 W/cm2 the temperature of the electron gas is 22K, approaching the critical temperature for Bose condensation of polaritons in our system (25 K). At higher pumping intensities, the electron-polariton interaction starts to play an important role, and the radiative efficiency of the polariton laser decreases due to scattering of the ground state polaritons with hot electrons. It should be mentioned that experimental evidences of the efficiency of electron scattering on polariton relaxation were recently ascertained Reference Tartakovskii[83] Reference Lagoudakis[84] Reference Cohen[85].

Figure 10. Radiative efficiency vs power absorbed in the microcavity at 10 K, for (a) a doped cavity, n e=1010 cm−2, (b) an undoped cavity, and (c) as (a) but including the effects of electron gas heating. The dotted part of the curve (b) corresponds to a calculated exciton density >5×1010 cm−2.
Finally, we propose a model GaN-based microcavity containing 9 GaN quantum wells (QWs) of 4 monolayer width each embedded inside the 3 λ/2 Al0.1Ga0.9N microcavity (see figure 11) Reference Malpuech, Di Carlo, Kavokin, Baumberg, Zamfirescu and Lugli[68]. The cavity is sandwiched between Al0.2Ga0.8N/Al0.9Ga0.1N Bragg mirrors having 11 pairs of λ/4 layers (upper mirror) and 14 pairs of λ/4 layers (bottom mirror). The structure is intended to be grown on a GaN substrate. An alternative possibility is to grow an oxide dielectric mirror on the top of the sample. The QWs are grouped by triplets at each antinode of the electric field of the microcavity eigenmode. All the parameters we use in the calculation are those of existing structures. Namely, the QW exciton energy (3543 meV), oscillator strength (0.6 meV) and inhomogeneous broadening (8 meV) are taken from Ref. Reference Zamfirescu, Gil, Grandjean, Malpuech, Kavokin, Bigenwald and Massies[86], although reduced inhomogeneous widths are now available. A single exciton resonance is considered. The refractive indices of AlGaN are taken from Ref. Reference Brunner, Angerer, Bustarret, Freudenberg, Höpler, Dimitrov, Ambacher and Stutzmann[87] Reference Bergmann, Ozgur, C Casey, Everitt and Muth[88]. The polariton dispersion relation of the microcavity for small wave vectors and for zero detuning between the exciton and the cavity mode is obtained by the scattering state method as shown on figure 3-b. A remarkable fact is that the vacuum-field Rabi-splitting between upper and lower polaritons exceeds 90 meV in our system which is larger than in any other semiconductors microcavity. Thus, the strong coupling in GaN microcavities is convincingly retained at room temperature which is one of the most important conditions for realisation of room-temperature polariton lasers.
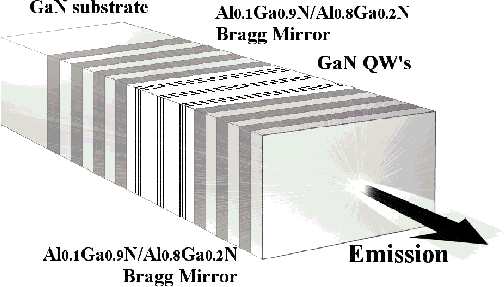
Figure 11. Schematic proposed GaN-based polariton laser.

Figure 12. Solid lines: exciton-polariton kinetic distribution functions of the GaN microcavity under non-resonant cw optical pumping at 300 K. The pump power densities used are (a) 1000 W/cm2 and (b) 40000 W/cm2. Black points and open circles show the values of the distribution function for the lowest energy states (assuming the exciting light spot is 50 μm radius) for pump densities of 1000 W/cm2 and 40000 W/cm2, respectively. Dashed line shows the Bose-Einstein polariton distribution function of the same microcaity assuming a vanishing chemical potential. Inset shows the radiative efficiency of the polariton laser versus the pumping power density at 300 K.
Figure 12 shows the equilibrium distribution functions of the exciton-polaritons in our cavity at the cw non-resonant excitation density of (a) 1000 W/cm2 or (b) 40000 W/cm2. A free electron density of 1011 cm−2 is assumed. The dynamics of the distribution function is found as a solution of equation (9.1). The discrete nature of the reciprocal space is taken into account for the lowest energy states corresponding to k=0, k=2π/R, … At the small excitation density (a) the population of the polariton ground state n0 is approximately unity, marking the threshold to the bosonic amplification regime. For a large excitation density (b), n0 ≈ 104. In this case the Bose condensation of the MC polaritons is definitely achieved, as one concludes when comparing the curve (b) with the Bose-Einstein distribution function of the exciton-polaritons for μ=0 (dashed line). The radiative efficiency of the laser versus pumping power is presented in the inset. It shows a clear threshold amplification at the extremely low power of 100 mW and a quantum efficiency close to 50%. Smaller area devices have a correspondingly smaller threshold power, so we envisage thresholds below 1mW. This simulation shows that a new generation of optoelectronic devices called polariton lasers based on the Bose-condensation of MC polaritons, can be realised with use of n-doped microcavities based on GaN materials. The model polariton laser we have considered here is based on current technologies and shows an extremely low threshold power at room temperature and a high quantum efficiency.
10 Conclusions
In this article we have reviewed and commented on experimental and theoretical works performed to evidence light-exciton strong coupling and polariton lasing or polariton transition to a superfluid phase in semiconductor microcavities. Our main conclusions are as follow:
-
1. Cavity polaritons seem to be much more suitable than excitons weakly coupled to light for observation of bosonic effects because they are much less sensitive to structural imperfections of real structures. Exciton-polaritons do behave as weakly interacting bosons as it has been experimentally proved by Saviddis and Baumberg Reference Houdre, Stanley, Oesterle, Ilegems, Weisbuch and de Physique[15]. A few weeks ago, a coherence buildup in a non resonantly pumped microcavity has even been reported Reference Fisher and Hohenberg[48]. This result still needs to be confirmed.
-
2. Cavity polaritons cannot Bose condense because they are 2D particles. They are subject to the Kosterlitz-Thouless phase transition towards a superfluid phase and to local quasi-condensation permitting polariton lasing with critical temperatures larger than 300 K in large band gap semiconductors microcavities. These effects cannot be observed for bulk polaritons.
-
3. The size of quasi-condensation droplets at their percolation transition strongly depends on temperature and concentration of polaritons at the transition points. In the most usual experimental situation of rather low polariton concentration and low temperature, the local BEC within the laser spot takes place before the KT transition.
-
4. One of the most important obstacles on the way towards realisation of a working polariton laser is the kinetic blocking of the polariton relaxation (“bottleneck effect”). Our simulations show that this effect can be suppressed if a low concentration of free electrons is introduced in the system because of an efficient electron-polariton scattering present in this case. Also, at room temperature, if the strong coupling regime holds, polariton relaxation with acoustic phonons is expected to be much more efficient than at low temperatures.
-
5. Cavity polariton quasi-condensation is not only a fundamental effect, but it has quite important application perspectives. A polariton laser is strictly speaking a zero threshold laser. Strong non-linear effects based on bosonic properties of cavity polaritons could form the physical basis of a future generation of optoelectronic devices.
-
6. Gallium nitride seems to be one of the most suitable materials for realisation of room-temperature polariton lasers. Other candidates could be CdSe, ZnO and organic materials.
It is worth mentioning that there remains still a long way to go before experimental realisation of a polariton laser and building of its complete theory. From the experimental point of view the main steps are the fabrication of cavities that would exhibit strong exciton-light coupling at room temperature and the systematic study of the kinetics of polariton relaxation both in doped and undoped cavities. An improvement of mirrors quality increasing polariton lifetime would also be extremely helpful. From the theoretical point of view, the quantum theory of polariton lasing should be developed in order to describe formation of the coherent state at k=0, the coherence of light emitted by condensed polaritons and spin relaxation in the Bose-gas of polaritons. The role of exciton localisation and scattering in microcavities should be clarified.
Acknowledgments
We wish to thank Aldo Di Carlo, Jeremy J. Baumberg, Pavlos Lagoudakis, Pierre Bigenwald, Fabrice Laussy, Yuri Rubo and Marian Zamfirescu for all the fruitful discussions we had together on the topic of this article.
Appendices
1 Transfer matrix method for a light wave propagating in a planar structure
Here we describe the transfer matrix method to obtain the solution of the wave-equation for light propagating in planar structures. Most frequently, bases of tangential components of electric and magnetic fields and amplitudes of light waves propagating in positive and negative directions are considered. In these two bases the transfer matrix looks different. Note, that a variety of similar techniques is used to solve Maxwell or Schroedinger equations in planar structures, in particular, the scattering matrix method is a common encounter. We do not use this method in the paper and do not describe it here.
Appendix 1.1
Basis of tangential components of electric and magnetic fields
Consider a light-wave propagating along z-direction in a media characterized by a refractive index n homogeneous in the xy plane but possibly z-dependent. The wave equation reads in this case:
where k0 is the wave-vector of light in vacuum. We will chose two linearly independent solutions of Equation (A1) y1(z), y2(z) subject to the set of boundary conditions:
where k = k0n. The transfer matrix

If n is a constant across the layer a, y 1(z)=coskz y 2(z), and

It is easy to check that for a vector

where E(z), H(z) are the amplitudes of electric and magnetic field of any light wave propagating in z direction in the structure under study, the condition if fulfilled:
Note that
where
The transfer matrix across a layer can be expressed via reflection r and trasmission t coefficients of this layer. If reflection and transmission coefficients for light incident from right-hand side and left-hand side on the layer are the same (symmetric case realized, in particular, in a QW embedded in a cavity) condition (A6) yields:

In (A8) the first equation is written for the light incident from the left and the second equation is written for the light incident from the right. nis the refractive index of the surrounding media. It allows to express the matrix

Appendix 1.2
Basis of amplitudes of light-waves propagating towards z=+∞ and z=−∞
A solution of Equation (A1) can be formally represented as:
where E+(−)(z) is the complex amplitude of light-wave propagating in positive (negative) direction. One can define the transfer matrix
Consider a few particular cases.
If the refractive index n is constant across the layer a, the transfer matrix has a simple form:
The transfer matrix across an interface between a media having the refractive index n 1 and a media having the refractive index n 2 is
It can be obtained with use of the condition (B2) applied to the light waves incident from the left side and right side of the interface and bearing in mind the well-known expressions for the reflection and transmission coefficients of interfaces. In a similar way, the transfer matrix across a symmetric object (QW embedded in the cavity, for instance) can be written as:
where r and t are amplitude reflection and transmission coefficients of the object.
Appendix 1.4
Photonic bands of 1D periodic structures
Consider an infinite structure whose refractive index is homogeneous in the (xy)-plane and its dependence on the coordinate z is a periodical function having a period d. The shape of this function is not essential, we will only assume that a transfer matrix
where
where UE,H(z) have the periodicity of the structure and Q is, in general, a complex number. Note that the factor eiQz is the same for electric (E) and magnetic (H) fields in a light wave because in the normal incidence case they are linked by:
Substitution of ((C2)) into ((C1)) yields
thus eiQd is an eigen-value of the matrix
where
Thus we reduce equation (C4) to
and T ij are elements of the matrix
Right part of this equation is frequency-dependent. Frequency bands for which
are allowed photonic bands. In them Q is purely real, and the light wave can propagate freely without attenuation. Conversely, the bands for which
are usually called stop-bands or optical gaps. In them Q has a non-zero imaginary part which determines the decay of propagating light-waves. All this is completely analogous to conventional crystals. Eqs. ((C7), (C8), (C9)) are valid also in the oblique incidence case while the form of the matrix















