Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T23:37:09.799Z Has data issue: false hasContentIssue false
  • English
  • Français

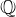Computing cardinalities of $\mathbb{Q}$-curve reductions over finite fields

Part of: Computational number theory Arithmetic algebraic geometry

Published online by Cambridge University Press:  26 August 2016

François Morain ,
Charlotte Scribot  and
Benjamin Smith
François Morain
Affiliation:
École Polytechnique/LIX, and Centre national de la recherche scientifique (CNRS), and Institut national de recherche en informatique et en automatique (INRIA), France email morain@lix.polytechnique.fr
Charlotte Scribot
Affiliation:
Ministère de l’Éducation Nationale, France
Benjamin Smith
Affiliation:
Institut national de recherche en informatique et en automatique (INRIA), and École Polytechnique/LIX, and Centre national de la recherche scientifique (CNRS), France email smith@lix.polytechnique.fr

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a specialized point-counting algorithm for a class of elliptic curves over 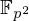$\mathbb{F}_{p^{2}}$ that includes reductions of quadratic 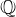$\mathbb{Q}$-curves modulo inert primes and, more generally, any elliptic curve over 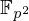$\mathbb{F}_{p^{2}}$ with a low-degree isogeny to its Galois conjugate curve. These curves have interesting cryptographic applications. Our algorithm is a variant of the Schoof–Elkies–Atkin (SEA) algorithm, but with a new, lower-degree endomorphism in place of Frobenius. While it has the same asymptotic asymptotic complexity as SEA, our algorithm is much faster in practice.

MSC classification

Primary: 11Y16: Algorithms; complexity
Secondary: 11G20: Curves over finite and local fields 11G05: Elliptic curves over global fields
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 115 - 129
Copyright
© The Author(s) 2016 

References

Bostan, A., Morain, F., Salvy, B. and Schost, É., ‘Fast algorithms for computing isogenies between elliptic curves’, Math. Comp. 77 (2008) no. 263, 1755–1778.Google Scholar
Cheng, Q., ‘Straight-line programs and torsion points on elliptic curves’, Comput. Complexity 12 (2003) 150–161.CrossRefGoogle Scholar
Costello, C., Hisil, H. and Smith, B., ‘Faster compact Diffie–Hellman: endomorphisms on the x-line’, Advances in cryptology – EUROCRYPT 2014 – Proceedings of the 33rd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Copenhagen, Denmark, May 11–15, 2014 , Lecture Notes in Computer Science 8441 (eds Nguyen, P. Q. and Oswald, E.; Springer, Berlin, 2014) 183–200.Google Scholar
Costello, C. and Longa, P., ‘Fourℚ: four-dimensional decompositions on a ℚ-curve over the Mersenne prime’, Advances in cryptology – ASIACRYPT 2015 – 21st International Conference on the Theory and Application of Cryptology and Information Security, Auckland, New Zealand, November 29–December 3, 2015, Proceedings, Part I , Lecture Notes in Computer Science 9452 (eds Iwata, T. and Cheon, J. H.; Springer, Berlin, 2015) 214–235.Google Scholar
Couveignes, J.-M. and Morain, F., ‘Schoof’s algorithm and isogeny cycles’, Algorithmic number theory, 1st Algorithmic Number Theory Symposium, Cornell University, May 6–9, 1994 , Lecture Notes in Computer Science 877 (eds Adleman, L. and Huang, M.-D.; Springer, Berlin, 1994) 43–58.Google Scholar
Fouquet, M. and Morain, F., ‘Isogeny volcanoes and the SEA algorithm’, Algorithmic number theory, Proceedings of the 5th International Symposium, ANTS-V, Sydney, Australia, July 2002 , Lecture Notes in Computer Science 2369 (eds Fieker, C. and Kohel, D. R.; Springer, Berlin, 2002) 276–291.Google Scholar
von zur Gathen, J. and Gerhard, J., Modern computer algebra (Cambridge University Press, Cambridge, 1999).Google Scholar
Gaudry, P. and Morain, F., ‘Fast algorithms for computing the eigenvalue in the Schoof–Elkies–Atkin algorithm’, ISSAC ’06: Proceedings of the 2006 International Symposium on Symbolic and Algebraic Computation (ACM Press, New York, NY, 2006) 109–115.Google Scholar
González, J., ‘Isogenies of polyquadratic ℚ-curves to their Galois conjugates’, Arch. Math. 77 (2001) 383–390.Google Scholar
Guillevic, A. and Ionica, S., ‘Four-dimensional GLV via the Weil restriction’, Advances in cryptology – ASIACRYPT 2013 , Lecture Notes in Computer Science 8269 (eds Sako, K. and Sarkar, P.; Springer, 2013) 79–96.CrossRefGoogle Scholar
Hasegawa, Y., ‘Q-curves over quadratic fields’, Manuscripta Math. 94 (1997) no. 1, 347–364.Google Scholar
Joux, A. and Lercier, R., ‘Chinese & match, an alternative to Atkin’s match and sort method used in the SEA algorithm’, Math. Comp. 70 (2001) no. 234, 827–836.CrossRefGoogle Scholar
Kaltofen, E. and Shoup, V., ‘Subquadratic-time factoring of polynomials over finite fields’, Math. Comp. 67 (1998) no. 223, 1179–1197.Google Scholar
Lercier, R., ‘Finding good random elliptic curves for cryptosystems defined over F2 n ’, Advances in cryptology – EUROCRYPT ’97 , Lecture Notes in Computer Science 1233 (ed. Fumy, W.; Springer, Berlin, 1997) 379–392.CrossRefGoogle Scholar
Mihăilescu, P., Morain, F. and Schost, É., ‘Computing the eigenvalue in the Schoof–Elkies–Atkin algorithm using Abelian lifts’, ISSAC ’07: Proceedings of the 2007 International Symposium on Symbolic and Algebraic Computation (ACM Press, New York, NY, 2007) 285–292.Google Scholar
Sako, K. and Sarkar, P. (eds), Advances in cryptology – ASIACRYPT 2013 , Lecture Notes in Computer Science 8269 (Springer, 2013).Google Scholar
Satoh, T., ‘On p-adic point counting algorithms for elliptic curves over finite fields’, Algorithmic number theory, Proceedings of the 5th International Symposium, ANTS-V, Sydney, Australia, July 7–12, 2002 , Lecture Notes in Computer Science 2369 (eds Fieker, C. and Kohel, D. R.; Springer, 2002) 43–66.Google Scholar
Schoof, R., ‘Elliptic curves over finite fields and the computation of square roots mod p ’, Math. Comp. 44 (1985) 483–494.Google Scholar
Schoof, R., ‘Nonsingular plane cubic curves over finite fields’, J. Combin. Theory Ser. A 46 (1987) no. 2, 183–211.Google Scholar
Schoof, R., ‘Counting points on elliptic curves over finite fields’, J. Théor. Nombres Bordeaux 7 (1995) 219–254.CrossRefGoogle Scholar
Shparlinski, I. E. and Sutherland, A. V., ‘On the distribution of Atkin and Elkies primes’, Found. Comput. Math. 14 (2014) no. 2, 285–297.CrossRefGoogle Scholar
Shparlinski, I. E. and Sutherland, A. V., ‘On the distribution of Atkin and Elkies primes for reductions of elliptic curves on average’, LMS J. Comput. Math. 18 (2015) no. 1, 308–322.Google Scholar
Smith, B., ‘Families of fast elliptic curves from ℚ-curves’, Advances in cryptology – ASIACRYPT 2013 , Lecture Notes in Computer Science 8269 (eds Sako, K. and Sarkar, P.; Springer, 2013) 61–78.Google Scholar
Smith, B., ‘The ℚ-curve construction for endomorphism-accelerated elliptic curves’, J. Cryptology (2015).Google Scholar
Sutherland, A. V., ‘Identifying supersingular elliptic curves’, LMS J. Comput. Math. 15 (2012) 317–325.CrossRefGoogle Scholar
Sutherland, A. V., ‘On the evaluation of modular polynomials’, ANTS X—Proceedings of the Tenth Algorithmic Number Theory Symposium, Open Book Series 1 (Mathematical Science Publishers, Berkeley, CA, 2013) 531–555.Google Scholar
Zhu, H. J., ‘Group structures of elementary supersingular abelian varieties over finite fields’, J. Number Theory 81 (2000) 292–309.CrossRefGoogle Scholar