Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-18T08:48:10.378Z Has data issue: false hasContentIssue false
  • English
  • Français

Computation of Mordell–Weil bases for ordinary elliptic curves in characteristic two

Part of: Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  01 August 2014

G. Moehlmann
G. Moehlmann*
Affiliation:
Institut für Mathematik, Technische Universität Berlin, Straße des 17. Juni 136, D-10623 Berlin, Germany email moehlman@math.tu-berlin.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider ordinary elliptic curves over global function fields of characteristic 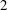$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}2$. We present a method for performing a descent by using powers of the Frobenius and the Verschiebung. An examination of the local images of the descent maps together with a duality theorem yields information about the global Selmer groups. Explicit models for the homogeneous spaces representing the elements of the Selmer groups are given and used to construct independent points on the elliptic curve. As an application we use descent maps to prove an upper bound for the naive height of an 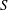$S$-integral point on 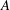$A$. To illustrate our methods, a detailed example is presented.

MSC classification

Secondary: 11G05: Elliptic curves over global fields 11G07: Elliptic curves over local fields 14G25: Global ground fields 14G17: Positive characteristic ground fields
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Special Issue A: Algorithmic Number Theory Symposium XI , 2014 , pp. 1 - 13
Copyright
© The Author 2014 

References

Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: the user language’, J. Symbolic Comput. 24 (1997) no. 3/4, 235–265.CrossRefGoogle Scholar
Broumas, A., ‘Effective p-descent’, PhD Thesis, University of Texas, 1995.Google Scholar
Broumas, A., ‘Effective p-descent’, Compos. Math. 107 (1997) 125–141.CrossRefGoogle Scholar
Cremona, J. E., Fisher, T. A. and Stoll, M., ‘Minimisation and reduction of 2-, 3- and 4-coverings of elliptic curves’, Algebra Number Theory 4 (2010) 763–820.CrossRefGoogle Scholar
Cremona, J. E., Prickett, M. and Siksek, S., ‘Height difference bounds for elliptic curves over number fields’, J. Number Theory 116 (2006) no. 1, 42–68.Google Scholar
Gebel, J., Pethő, A. and Zimmer, H., ‘Computing integral points on elliptic curves’, Acta Arith. 68 (1994) no. 2, 171–192.CrossRefGoogle Scholar
Kramer, K., ‘Two-descent for elliptic curves in characteristic two’, Trans. Amer. Math. Soc. 232 (1977) 279–295.CrossRefGoogle Scholar
Milne, J. S., Arithmetic duality theorems, 2nd edn (BookSurge, 2006).Google Scholar
Shatz, S., ‘Cohomology of Artinian group schemes over local fields’, Ann. of Math. (2) 79 (1963) no. 3, 411–449.CrossRefGoogle Scholar
Siksek, S., ‘Descent on curves of genus 1’, PhD Thesis, University of Exeter, 1995.Google Scholar
Silverman, J. H., The arithmetic of elliptic curves (Springer, 1986).CrossRefGoogle Scholar
Silverman, J. H., ‘The difference between the Weil height and the canonical height on elliptic curves’, Math. Comp. 55 (1990) 723–743.CrossRefGoogle Scholar
Simon, D., Equations dans les corps de nombres et discriminants minimaux’, PhD Thesis, Université Bordeaux, 1998.Google Scholar
Thomas, L., ‘Ramification groups in Artin–Schreier–Witt extensions’, J. Théor. Nombres Bordeaux 17 (2005) 689–720.CrossRefGoogle Scholar
Ulmer, D., ‘Elliptic curves with large rank over function fields’, Ann. of Math. (2) 155 (2002) 295–315.CrossRefGoogle Scholar
Ulmer, D., ‘p-descent in characteristic p’, Duke Math. J. 62 (1991) 237–265.Google Scholar
Voloch, J. F., ‘Explicit p-descent for elliptic curves in characteristic p’, Compos. Math. 74 (1990) 247–258.Google Scholar
Womack, T., ‘Explicit descent on elliptic curves’, PhD Thesis, University of Nottingham, 2003.Google Scholar