1. INTRODUCTION
Despite the great success in development of high-peak-power laser systems and the attainment of the peak intensity of 1022 W/cm2 (Mourou & Tajima, Reference Mourou and Tajima2011, and references therein; Bahk et al., Reference Bahk, Rousseau, Planchon, Chvykov, Kalintchenko, Maksimchuk and Yanovsky2005) the diagnostics used to estimate the peak intensity still does not follow this progress to full extent. Intensity in the beam waist, being a combination of basic parameters of a laser radiation, can be derived from the pulse energy, temporal, and spatial characteristics, measured at lowered energy, and extrapolated to high energy/intensity level. Low accuracy of this method makes it difficult to compare experimental results achieved at different laser facilities. Some of recompression errors that are specific for the chirped pulse amplification technique, as a tilted front for instance, are hardly to be visible. This can lead to substantial errors in determination of the pulse duration in the focal region. Thus, development of an alternative method for estimation of focus intensity directly in the beam waist in the experimental chamber is of great importance for the high-intensity laser community.
Following the progress of laser facilities, during the last few years diagnostics of the peak intensity was investigated in several publications (Gao, Reference Gao2006; Link et al., Reference Link, Chowdhury, Morrison, Ovchinnikov, Offermann, Van Woerkom, Freeman, Pasley, Shipton, Beg, Rambo, Schwarz, Geissel, Edens and Porter2006; Hetzheim & Keitel, Reference Hetzheim and Keitel2009; Smeenk et al., Reference Smeenk, Salvail, Arissian, Corkum, Hebeisen and Staudte2011; Har-Shemesh & Di Piazza, Reference Har-Shemesh and Di Piazza2013; Ekanayake et al., Reference Ekanayake, Luo, Grugan, Crosby, Camilo, McCowan, Scalzi, Tramontozzi, Howard, Wells, Mancuso, Stanev, Decamp and Walker2013). One of the techniques involves in laser irradiation of a low-density noble gas target and the registration of multiple-stage ionization of the gas. Another method concerns analysis of the accelerated electrons and back Thomson/Compton scattering. Most of these methods work in relatively narrow ranges of laser intensity and require in addition external beams of nearly mono energetic electrons or ions of a definite ionization state. This, in addition, strongly narrows possibilities of using such the diagnostic techniques because of the required ability of corresponding additional sources of particles and cost issues.
In the current publication, we experimentally study an alternative approach, proposed theoretically recently (Galkin et al., Reference Galkin, Egorov, Kalashnikov, Korobkin, Romanovsky, Shiryaev, Trofimov and Vorobyev2009; Reference Galkin, Kalashnikov, Klinkov, Korobkin, Romanovsky and Shiryaev2010). This method is based on the measurement of energies of electrons, accelerated in the focal spot that carry residual energy comparable with the oscillations energy in the intense laser field. The electrons are created via the ionization process of a low-density gas target [their concentration is low enough to make the effects stemming from both the Coulomb interactions between the charged particles and the collisions between them negligible, as well as acceleration by plasma wake fields, treated by Geddes et al. (Reference Geddes, Toth, Van Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004), Mangles et al. (Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick2004), Faure et al. (Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004), Kando et al. (Reference Kando, Masuda, Zhidkov, Yamazaki, Kotaki, Kondo, Homma, Kanazawa, Nakajima, Hayashi, Mori, Kiriyama, Akahane, Inoue, Ueda, Nakai, Tsuji, Yamamoto, Yamakawa, Koga, Hosokai, Uesaka and Tajima2005), Leemans e t al. (Reference Leemans, Nagler, Gonsalves, Tóth, Nakamura, Geddes, Esarey, Schroeder and Hooker2006)]. Dynamics and energy distribution of electrons expelled from the interaction area are determined by the laser pulse parameters. Consequently, experimental measurement of the particle energy distribution can serve as an instrument of diagnosing the laser pulse parameters in the focal spot, in particular the maximum intensity. For a focused Gaussian beam several studies of laser-driven electron dynamics have been reported (Hartemann et al., Reference Hartemann, Fochs, Le Sage, Luhmann, Woodworth, Perry, Chen and Kerman1995; Pang et al., Reference Pang, Ho, Yuan, Cao, Kong, Wang, Shao, Esarey and Sessler2002; Wang et al., Reference Wang, Hua, Lin and Ho2002; Galkin et al., Reference Galkin, Galstian, Korobkin, Romanovsky and Shiryaev2007a; Reference Galkin, Korobkin, Romanovsky and Shiryaev2007b). It was shown that for a certain period of time the electron remains trapped by the laser pulse and moves with it along the pulse propagation axis (Pang et al., Reference Pang, Ho, Yuan, Cao, Kong, Wang, Shao, Esarey and Sessler2002; Wang et al., Reference Wang, Hua, Lin and Ho2002; Galkin et al., Reference Galkin, Korobkin, Romanovsky and Shiryaev2007b). This approach does not require any additional target or a particle beam and can be used on an everyday basis for a fast control of the laser system.
2. EXPERIMNENTAL SETUP
The experiments were done with a 100 TW High-Field laser system in Max-Born-Institute, Berlin. The laser system running at 10 Hz delivered pulse with energy up to 3 J, duration of ~30 fs, that was focused with an off-axis parabolic mirror (F/D = 5) in a spot with diameter of 2.2 ± 0.1 μm at full width at half maximum and containing about 15% of total energy (see Fig. 1a). Initially the maximum peak intensity was evaluated from the energy and spatio-temporal distribution of radiation in the focal area. As a result, the estimation of the peak intensity gave the value of ~3 × 1020 W/cm2.
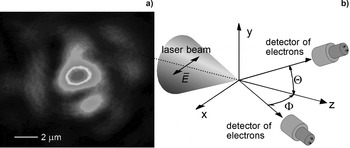
Fig. 1. (a) Distribution of laser intensity in the beam waist. (b) Scheme of the experimental setup.
The scheme of the experimental setup is shown in Figure 1b. The recompressed laser beam polarized in the X-direction was focused in a chamber filled with a gas at a pressure of 10−5 – 10−3 mbar. Three types of gases [helium (He), argon (Ar), and krypton (Kr)] were used in experiments. The spectra of accelerated electrons were measured by a 1 cm thick plastic scintillator-based detector with a photomultiplier (PMT) and an analyzer. The detector had linear energy sensitivity in the range from ~0.3 to ~2 MeV and the energy resolution of 15%. The electron spectrometer was calibrated with a Sr-90 beta source. The detector worked in a counting mode measuring ~0.3 events per laser shot. During the experiments vacuum pumps of the experimental chamber and the gas flow were permanently running. The spectra were accumulated over 10.000 laser shots at constant pressure. The detector could be placed outside the vacuum chamber behind vacuum flanges covered by a thin (13 μm) mylar foil. Several directions in the X–Z plane with angles Ф of 70°, 35°–55°, 22°, 0°–5° relative to the Z-axis and one at ϑ~40° in the Y–Z plane were available for experimenting with angle coverage dФ (or dϑ) of <1°.
3. EXPERIMENTAL RESULTS
Results of experiments can be summarized as follows. First, the measurements of electron spectra in the X–Z and Y–Z planes at the same angle (Φ = ϑ ≈ 40°) approved that the electron spectra are independent of polarization of the incident laser light. In the second series of experiments different gases were tested.
Starting with He, we found that the counting rate decreased gradually with time after turning the laser on. This degradation resulted from the fact that the recombination time at the given gas pressure (~10−3 mbar) is large and can be estimated at the level of about 100 s. This behavior was also observed with other gases (e.g., Ar and Kr), however, at a much lesser extent. The impact of this effect was reduced by choosing a quasi-periodic run of the experiment. The laser was turned on for a period of 50 s until the moment when the counting rate started to decrease. A pause of 5 min followed for recombination of ionized gas. After several tens of cycles the electron spectra taken at the same experimental conditions were summarized and processed using Monte-Carlo simulations of electron interaction with a scintillation medium based on CASINO code to take into account the detector efficiency (Drouin et al., Reference Drouin, Couture, Joly, Tastet, Aimez and Gauvin2007).
It is worth mentioning that we did not find any substantial difference in the electron spectra taken with Ar and Kr, which insured us that the ionization process did not have a substantial impact in our experiment and we were not above the full ionization of Ar. Two main features were observed (raw experimental spectra are presented in Fig. 2a–2c): At low energies (up to ~500 keV, depending on the observation angle) a tailing off electron distribution was registered. In addition, a broad peak with the central energy expanding in a MeV range appeared when we moved closer to the Z-axis. Both parts of spectra disappeared, when a thick, light-transparent plastic absorber was placed in front of the detector. This ensured that the measured signal was coming from electrons.
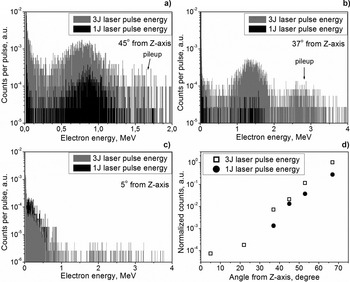
Fig. 2. Raw electron spectra, measured at 45° (a), 37° (b), and 5° (c) relative to the laser beam in the plane of the pulse polarization (X–Z). The laser pulse energy – 1 J (black columns) and 3 J (gray columns). The background gas Ar had a pressure of 3 × 10−4 mbar. (d) Dependence of the total number of particles emitted from the focal area on the angle of observation relative to the laser wave vector in the plane of the pulse polarization (X–Z). Detector efficiency is taken into account.
Since the detector cut-off in the low-energy range is about 300 keV due to absorption in the window of the vacuum chamber, air, and a thin filter in front of the detector, the low-energy falling part may be related to the contribution of scattered particles. However, for the spectra taken at small angle (5°), the falling part extends to 1 MeV and must be treated as the net electron signal (in the range above the cut-off energy).
The experimental results showed that the electrons with maximum energy are observed at smaller angles. The broad peak appeared at angle of 3°–5° for the pulse energy of 3 J with the maximum registered electron energy about 4 MeV (see Fig. 2c). This energy does not depend on the gas pressure inside the vacuum chamber. It is worth mentioning that this value may be even higher due to uncertainty of particle energy determination with our detector in the range above ~2–2.5 MeV. The stopping power for electrons in plastic is ~2 MeV/cm. Hence, almost all particles with higher energies passing through our 1 cm thick detector could contribute only with a part of their energy. For the pulse energy of 1 J the broad peak at small angles was not observed. The particles having the maximum energy of ~1 MeV were registered in the falling part of the spectrum. The absolute number of accelerated electrons in the broad peak exponentially decreases approaching the Z-axis; see Figure 2d.
4. COMPARISON WITH THEORY
To analyze the experimental data and to explain the observed effects we used a modified two-dimensional particle-in-cell (2D-PIC) code (Andreev et al., Reference Andreev, Steinke, Sokollik, Schnurer, Ter Avetisyan, Platonov and Nickles2009). We considered propagation of a Gaussian-shaped laser pulse with intensity I = 1019–1022 W/cm2 in the Ar plasma of ion density n i = 1014 cm−3 along the Z-axis. Dependence of the average charge of Ar atoms on the laser intensity was taken from the model (Delone & Krainov, Reference Delone and Krainov2001; Amosov et al., Reference Amosov, Delone and Krainov1986). The pulse duration t L = 40 fs and the beam diameter d L = 10 μm. The size of the simulation box was 100 × 100 μm2, and grid size 40 nm. The time step was 0.1 fs and 20 particles per cell were taken.
The simulation showed that the particles distribution in the space of momenta (p y, pz) displayed in Figure 3a has the form of a parabola, which shape is conserved for varied intensities. The particles with higher energies are observed at a smaller angle relative to the beam axis. This elucidates appearance of a broad peak in the experimental spectra with central energy, increasing at smaller angles.
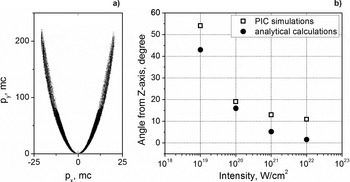
Fig. 3. (a) The momenta distribution of electrons propagating out of the focal volume at laser intensity 1020 W/cm2. (b) The position of the maximum of angular electron density distribution (open squares – simulation results) and angle φ of single electron propagation in a plane wave (closed circles – analytical results).
The concentration of electrons in the parabola arms is strongly dependent on laser intensity. A maximum of electron density moving toward the Z-axis with the intensity growth is observed (Fig. 3b), which is in a good agreement with the analytical formula considering propagation of a single electron in a plane wave: ϕ = arctg(2/a), where ![]() $a = \sqrt {0.6 \times I\, {\rm \lambda} _{{\rm \mu m}}^2 /10^{18} {\rm W}/{\rm cm}^2} $ (Landau et al., Reference Landau and Lifshitz1971).
$a = \sqrt {0.6 \times I\, {\rm \lambda} _{{\rm \mu m}}^2 /10^{18} {\rm W}/{\rm cm}^2} $ (Landau et al., Reference Landau and Lifshitz1971).
However, in the experiment we do not observe a maximum in angular distribution of electrons (Fig. 2d). This discrepancy may be attributed to the fact, that in the simulations only the particles generated in the beam waist were taken into account, whereas in the experiment the electrons expelled from a much wider area around the focal spot could be registered. It is also worth mentioning, that in the direction of laser pulse propagation a large number of particles with energies up to few MeV, trapped by the pulse at different moments of time, were observed. This fact explains the presence of the quasi-exponential part in the experimental spectra at small angles.
The measurement of particles with the highest energy at a small angle may be used to determine the peak intensity. In our experiment, however, this technique could not be used because for the peak intensity above 1020 W/cm2 this requires to measure electrons in the energy band of several tens of MeV that was not possible with our detector.
To estimate the peak intensity in the focus we use the method proposed earlier (see Galkin et al., Reference Galkin, Kalashnikov, Klinkov, Korobkin, Romanovsky and Shiryaev2010). According to this model the energy distribution of the expelled from the waist particles exhibits an exponential tail with an effective electron temperature, determining both the peak laser intensity and the caustic parameter ρ0/λ, where ρ0 is the waist size. Thus, both the values can be derived from the ratio of experimentally measured mean values of the effective temperature taken in two experiments at slightly different levels of laser energy. In particular, these dependences calculated for different values of laser intensity and the caustic parameter ρ0/λ are presented in Figure 4b. Parameter S = (I m/I r)(ρ0/λ), where I m-intensity realized in the experiment, I r = 1.37 × 1018 [1/λ(m)]2(W/cm2) – relativistic intensity. The experimental spectra integrated over the angles Ф form quasi-exponential distributions are presented in Figure 4a. The data after that were processed by a Monte-Carlo simulation by taking into account the detector efficiency. This allowed one to determine the slope of the distribution or the effective temperature. This procedure was applied to experimental data taken at two values of the laser energy (1 and 3 J) for Ar as the background gas at a pressure of 3 × 10−4 mbar. Calculated this way the effective temperatures Θ (in units of mc2) had the values of 0.80 ± 0.05 for 3 J, and 0.56 ± 0.04 for 1 J. The results of PIC simulations have shown that the electron distribution functions at time longer than 100 fs can be characterized by two or three components (cold and hot) with different temperatures. The cold component has temperature slightly below MeV that corresponds well with the observed experiment values and the hot components a few times higher. Also there is the dependence of the temperature on the angle of observation. The temperature decreases at bigger angles with respect to the laser axis.
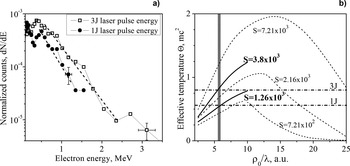
Fig. 4. (a) Electron spectra integrated over angles Ф for 1 J (circles) and 3 J (open squares) pulses. The solid red lines schematically depict the fit of the slopes. (b) Calculation of the laser beam caustic waist radius ρ0/λ using the Θ value based on the Θ(ρ0/λ) dependence for different pulse total power S. See all notations in Figure 7 of Galkin et al. (Reference Galkin, Kalashnikov, Klinkov, Korobkin, Romanovsky and Shiryaev2010). The horizontal solid straight lines correspond to evaluated Θ at 3 and 1 J laser energy. The vertical gray line denotes the obtained value ρ0/λ.
Now, taking the given above mean values of effective temperatures, one gets that the experimental results fit the curves S 1 = 3.8 × 103 and S 2 = 1.26 × 103 (that correspond to laser pulse energies of 3 and 1 J) in the point ρ0/λ = 5.7 ± 0.5 (see Fig. 4b). Taking into account that the relation between the maximum intensity and the parameter S is I m = I r × S × (λ/ρ0 )2, where the value of relativistic intensity taken at 800 nm is I r(800 nm) = 2.14 × 1018 W/cm2. Finally one gets the value of the peak intensity achieved in the experiment for the incident laser energy of 3 J: I m = (2.5 ± 0.4) × 1020 W/cm2. The accuracy of the proposed method is mainly defined by the error in evaluation of the effective temperature Θ. This value for the case of a given pulse energy does not exceed 10%. Since our method requires two measurements of Θ taken at different laser energies (1 and 3 J in our case), we estimate the total error below 20%. Despite that this value is slightly higher than that reported by Har-Shemesh and Di Piazza (Reference Har-Shemesh and Di Piazza2013) and Smeenk et al. (Reference Smeenk, Salvail, Arissian, Corkum, Hebeisen and Staudte2011), our method has a great advantage – simplicity. Supplying the accuracy sufficient for many of laser–matter interaction experiments at relativistic intensity it does not require complicated and expensive diagnostics and additional equipment.
We are convinced that this method will work well for much higher intensity levels than were achieved in the current experiment. This can be testified experimentally using a wider range of laser parameters (pulse energy, duration, focusing, etc.). The current step toward development of a simple diagnostics to measure directly the laser intensity of a relativistic level may be useful in the rapidly developing field of ultra-relativistic laser systems.
At higher intensities, however, the experiments should be carried out at lowered (at least by two orders of magnitude) gas density to avoid nonlinear effects due to high electron concentration in the focal area. Other instruments for electron detection must be used as well to simplify the investigation of electron spectra at higher energies. It is worth mentioning that for the intensity level above 1022–1023 W/cm2 different quantum electrodynamics (QED) phenomena may be involved into the diagnostics, which is also interesting from the point of view of fundamental physics. For instance, it was shown previously, that at interaction of high-peak-power laser pulse with high-charged ions at rest the production of electron–positron pair may occur (Sieczka et al., Reference Sieczka, Krajewska, Kaminski, Panek and Ehlotzky2006). The consequent acceleration of electrons/positrons in the surrounding laser field may lead with a finite probability to the electromagnetic cascade, resulting in self-generation of electron–positron pair plasma at the intensity level below 1024–1025 W/cm2 (Bell & Kirk, Reference Bell and Kirk2008; Nerush et al., Reference Nerush, Kostyukov, Fedotov, Narozhny, Elkina and Ruhl2011). Thus, the strongly rarefied ionized target may serve as a seed for the QED effects.
5. SUMMARY
To summarize, a new method to determine the maximum laser pulse intensity based on the measurement of integrated over the observation angle spectra of electrons that were accelerated in the beam waist via ionization of a low-density gas was experimentally justified. The peak intensity in the focal region estimated from the theory was found to be 2.5 × 1020 W/cm2 that is in an agreement with a simple estimate of the peak intensity based on spatio-temporal characteristics of the pulse in the beam waist.
It was found that a broad peak with central energy increasing from a few hundred KeV up to several MeV is observed at angles ranging from 70° to 5° relative to the laser beam propagation axis. This is in agreement with PIC simulations of laser–low-density plasma interaction and the analytical model of acceleration of a single electron in an intense electromagnetic plane wave. The particles with the highest energy are accelerated toward the beam propagation axis, in consistence with the experimental results. This can be used as an additional method to measure the peak intensity of above the relativistic level in the beam waist.
ACKNOWLEDGMENTS
Authors acknowledge the provided computation resources of JSC at project HBU15. The work was financially supported by Alexander von Humboldt Foundation and BMBF, the Russian Federal Property Fund 13-03-01259, Deutsche Forschungsgemeinschaft within the program CRC/Transregio 18 and LASERLAB-EUROPE (grants agreement No. 284464, EC's Seventh Framework Program).






