Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-29T06:17:20.135Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIVERSAL MIXED ELLIPTIC MOTIVES

Part of: Curves (Co)homology theory Arithmetic algebraic geometry Cycles and subschemes $K$-theory in geometry

Published online by Cambridge University Press:  30 April 2018

Richard Hain  and
Makoto Matsumoto
Richard Hain
Affiliation:
Department of Mathematics, Duke University, Durham, NC 27708-0320, USA (hain@math.duke.edu)
Makoto Matsumoto
Affiliation:
Graduate School of Sciences, Hiroshima University, Hiroshima 739-8526, Japan (m-mat@math.sci.hiroshima-u.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we construct a 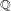$\mathbb{Q}$-linear tannakian category 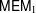$\mathsf{MEM}_{1}$ of universal mixed elliptic motives over the moduli space 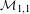${\mathcal{M}}_{1,1}$ of elliptic curves. It contains $\mathsf{MTM}$, the category of mixed Tate motives unramified over the integers. Each object of 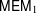$\mathsf{MEM}_{1}$ is an object of $\mathsf{MTM}$ endowed with an action of 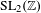$\text{SL}_{2}(\mathbb{Z})$ that is compatible with its structure. Universal mixed elliptic motives can be thought of as motivic local systems over 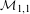${\mathcal{M}}_{1,1}$ whose fiber over the tangential base point 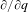$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}q$ at the cusp is a mixed Tate motive. The basic structure of the tannakian fundamental group of 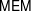$\mathsf{MEM}$ is determined and the lowest order terms of a set (conjecturally, a minimal generating set) of relations are deduced from computations of Brown. This set of relations includes the arithmetic relations, which describe the ‘infinitesimal Galois action’. We use the presentation to give a new and more conceptual proof of the Ihara–Takao congruences.

Keywords

mixed elliptic motivemixed Tate motivemodular curvemodular formelliptic polylogarithmvariation of mixed Hodge structure

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory 14F35: Homotopy theory; fundamental groups 14H52: Elliptic curves
Secondary: 11G55: Polylogarithms and relations with $K$-theory 14C30: Transcendental methods, Hodge theory , Hodge conjecture 19E20: Relations with cohomology theories
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 3 , May 2020 , pp. 663 - 766
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research was supported in part by the Scientific Grants-in-Aid 19204002, 23244002, 15K13460, JST-CREST 151001, and by the Core-to-Core grant 18005 from the Japan Society for the Promotion of Science; and grants DMS-0706955, DMS-1005675 and DMS-1406420 from the National Science Foundation.

References

Arapura, D., An abelian category of motivic sheaves, Adv. Math. 233 (2013), 135–195.Google Scholar
Ayoub, J., A Guide to (Étale) Motivic Sheaves, Proceedings of the International Congress of Mathematicians, Seoul 2014, Volume II, pp. 1101–1124 (Kyung Moon Sa, Seoul).Google Scholar
Baumard, S. and Schneps, L., On the derivation representation of the fundamental Lie algebra of mixed elliptic motives, Ann. Math. Qué. 41 (2017), 4362.Google Scholar
Beilinson, A., Higher Regulators and Values of L-Functions, Current Problems in Mathematics, Volume 24, pp. 181–238 (Itogi Nauki i Tekhniki, Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1984).Google Scholar
Beilinson, A., Higher regulators of modular curves, in Applications of Algebraic K-Theory to Algebraic Geometry and Number theory, Parts I, II (Boulder, CO, 1983), Contemporary Mathematics, Volume 55, pp. 1–34 (American Mathematical Society, Providence, RI, 1986).Google Scholar
Beilinson, A., Notes on absolute Hodge cohomology, in Applications of Algebraic K-Theory to Algebraic Geometry and Number Theory, Parts I, II (Boulder, CO, 1983), Contemporary Mathematics, Volume 55, pp. 35–68 (American Mathematical Society, Providence, RI, 1986).Google Scholar
Beilinson, A. and Levin, A., The elliptic polylogarithm, in Motives (Seattle, WA, 1991), Proc. Sympos. Pure Math., Volume 55, Part 2, pp. 123–190 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Borel, A., Cohomologie de SLn et valeurs de fonctions zeta aux points entiers, Ann. Sc. Norm. Super. Pisa Cl. Sci. 4 (1977), 613–636.Google Scholar
Brown, F., Multiple zeta values and periods of moduli spaces 𝓜0, n, Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 371–489.Google Scholar
Brown, F., Mixed Tate motives over ℤ, Ann. of Math. (2) 175 (2012), 949–976.Google Scholar
Brown, F., Multiple modular values for $\text{SL}_{2}(\mathbb{Z})$, Preprint, 2014, arXiv:1407.5167.Google Scholar
Brown, F., Zeta elements in depth 3 and the fundamental Lie algebra of the infinitesimal Tate curve, Forum Math. Sigma 5 (2017), e1, 56 pp.Google Scholar
Calaque, D., Enriquez, B. and Etingof, P., Universal KZB equations I: the elliptic case, in Algebra, Arithmetic, and Geometry: in Honor of Yu. I. Manin, Volume I, Progr. Math., Volume 269, pp. 165–266 (Birkhäuser, Boston, 2009).Google Scholar
Deligne, P., La conjecture de Weil, II, Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.Google Scholar
Deligne, P., Le groupe fondamental de la droite projective moins trois points, in Galois Groups Over ℚ (Berkeley, CA, 1987), Math. Sci. Res. Inst. Publ., Volume 16, pp. 79–297 (Springer, 1989).Google Scholar
Deligne, P., Le groupe fondamental unipotent motivique de 𝔾m -𝜇N, pour N = 2, 3, 4, 6 ou 8, Publ. Math. Inst. Hautes Études Sci. 112 (2010), 101–141.Google Scholar
Deligne, P. and Goncharov, A., Groupes fondamentaux motiviques de Tate mixte, Ann. Sci. Éc. Norm. Supér. (4) 38 (2005), 1–56.Google Scholar
Drinfeld, V., On quasitriangular quasi-Hopf algebras and on a group that is closely connected with Gal(ℚ/ℚ), Algebra i Analiz 2 (1990), 149–181; translation in Leningrad Math. J. 2 (1991), 829–860.Google Scholar
Enriquez, B., Elliptic associators, Selecta Math. (N.S.) 20 (2014), 491–584.Google Scholar
Fontaine, J.-M. and Perrin-Riou, B., Autour des conjectures de Bloch et Kato: cohomologie galoisienne et valeurs de fonctions L, in Motives (Seattle, WA, 1991), Proc. Sympos. Pure Math., Volume 55, Part 1, pp. 599–706 (American Mathematical Society, 1994).Google Scholar
Goncharov, A., Mixed elliptic motives, in Galois Representations in Arithmetic Algebraic Geometry (Durham, 1996), London Mathematical Society Lecture Note Series, Volume 254, pp. 147–221 (Cambridge University Press, 1998).Google Scholar
Goncharov, A., The dihedral Lie algebras and Galois symmetries of 𝜋1(ℓ)(¶1 - ({0, ∞}∪𝜇N)), Duke Math. J. 110 (2001), 397–487.Google Scholar
Hain, R., Hodge–de Rham theory of relative Malcev completion, Ann. Sci. Éc. Norm. Supér. 31 (1998), 47–92.Google Scholar
Hain, R., Relative weight filtrations on completions of mapping class groups, in Groups of Diffeomorphisms, Adv. Stud. Pure Mathematics, Volume 52, pp. 309–368 (Math. Soc., Japan, Tokyo, 2008).Google Scholar
Hain, R., Letter to P. Deligne, December, 2009.Google Scholar
Hain, R., Lectures on moduli spaces of elliptic curves, in Transformation Groups and Moduli Spaces of Curves, Adv. Lect. Math. (ALM), Volume 16, pp. 95–166 (International Press, 2011).Google Scholar
Hain, R., Notes on the Universal Elliptic KZB Equation, Pure and Applied Mathematics Quarterly, Volume 12, no. 2, (International Press, Somerville, MA, 2016).Google Scholar
Hain, R., The Hodge–de Rham theory of modular groups, in Recent Advances in Hodge Theory Period Domains, Algebraic Cycles, and Arithmetic (ed. Kerr, M. and Pearlstein, G.), LMS Lecture Notes Series, Volume 427, pp. 422–514 (Cambridge University Press, Cambridge, 2016).Google Scholar
Hain, R., Deligne–Beilinson cohomology of affine groups, in Hodge Theory and L 2 Methods (ed. Ji, L. and Zucker, S.), pp. 377–418 (International Press, Somerville, MA).Google Scholar
Hain, R., Unipotent path torsors of Ihara curves, in preparation.Google Scholar
Hain, R. and Matsumoto, M., Weighted completion of Galois groups and Galois actions on the fundamental group of ¶1 -{ 0, 1, ∞}, Compositio Math. 139 (2003), 119–167.Google Scholar
Hain, R. and Matsumoto, M., Tannakian fundamental groups associated to Galois groups, in Galois Groups and Fundamental Groups, Math. Sci. Res. Inst. Publ., Volume 41, pp. 183–216 (Cambridge University Press, 2003).Google Scholar
Hain, R. and Matsumoto, M., Relative pro-l completions of mapping class groups, J. Algebra 321 (2009), 3335–3374.Google Scholar
Hain, R. and Zucker, S., Unipotent variations of mixed Hodge structure, Invent. Math. 88 (1987), 83–124.Google Scholar
Hanamura, M., Mixed motives and algebraic cycles, I, Math. Res. Lett. 2 (1995), 811–821.Google Scholar
Ihara, Y., Some arithmetic aspects of Galois actions in the pro-p fundamental group of ¶1 -{ 0, 1, ∞}, in Arithmetic Fundamental Groups and Noncommutative Algebra (Berkeley, CA, 1999), Proceedings of Symposia in Pure Mathematics, Volume 70, pp. 247–273 (American Mathematical Society, 2002).Google Scholar
Jantzen, J. C., Representations of Algebraic Groups, Pure and Applied Mathematics, Volume 131 (Academic Press, 1987).Google Scholar
Katz, N. and Mazur, B., Arithmetic Moduli of Elliptic Curves, Annals of Mathematics Studies, Volume 108 (Princeton University Press, 1985).Google Scholar
Knudsen, F., The projectivity of the moduli space of stable curves, III. The line bundles on M g, n, and a proof of the projectivity of Mg, n in characteristic 0, Math. Scand. 52 (1983), 200–212.Google Scholar
Lang, S., Introduction to Modular Forms, with appendixes by D. Zagier and Walter Feit, Grundlehren der Mathematischen Wissenschaften, Volume 222 (Springer, 1995). Corrected reprint of the 1976 original.Google Scholar
Levine, M., Tate motives and the vanishing conjectures for algebraic K-theory, in Algebraic K-Theory and Algebraic Topology (Lake Louise, AB, 1991), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., Volume 407, pp. 167–188 (Kluwer, 1993).Google Scholar
Levine, M., Mixed Motives, Mathematical Surveys and Monographs, Volume 57 (American Mathematical Society, 1998).Google Scholar
Levin, A. and Racinet, G., Towards multiple elliptic polylogarithms, Preprint, 2007,arXiv:math/0703237.Google Scholar
Luo, M., The elliptic KZB connection and algebraic de Rham theory for unipotent fundamental groups of elliptic curves, Preprint, 2017, arXiv:1710.07691.Google Scholar
Nakamura, H., Tangential base points and Eisenstein power series, in Aspects of Galois Theory (Gainesville, FL, 1996), London Mathematical Society Lecture Note Series, Volume 256, pp. 202–217 (Cambridge University Press, 1999).Google Scholar
May, P., Matric Massey products, J. Algebra 12 (1969), 533–568.Google Scholar
Noohi, B., Fundamental groups of algebraic stacks, J. Inst. Math. Jussieu 3 (2004), 69–103.Google Scholar
Olsson, M., Towards non-abelian p-adic Hodge theory in the good reduction case, Mem. Amer. Math. Soc. 210(990) (2011), vi+157 pp.Google Scholar
Pollack, A., Relations between derivations arising from modular forms, undergraduate thesis, Duke University, 2009. Available at: http://dukespace.lib.duke.edu/dspace/handle/10161/1281.Google Scholar
Schmid, W., Variation of Hodge structure: the singularities of the period mapping, Invent. Math. 22 (1973), 211–319.Google Scholar
Schneps, L., On the Poisson bracket on the free Lie algebra in two generators, J. Lie Theory 16 (2006), 19–37.Google Scholar
Scholl, A., Motives for modular forms, Invent. Math. 100 (1990), 419–430.Google Scholar
Silverman, J., The Arithmetic of Elliptic Curves, Graduate Texts in Mathematics, Volume 106 (Springer, 1986).Google Scholar
Silverman, J., Advanced Topics in the Arithmetic of Elliptic Curves, Graduate Texts in Mathematics, Volume 151 (Springer, New York, 1994).Google Scholar
Soulé, C., On higher p-adic regulators, in Algebraic K-Theory, Evanston 1980 (Proc. Conf., Northwestern University, Evanston, IL, 1980), Lecture Notes in Mathematics, Volume 854, pp. 372–401 (Springer, 1981).Google Scholar
Steenbrink, J. and Zucker, S., Variation of mixed Hodge structure, I, Invent. Math. 80 (1985), 489–542.Google Scholar
Takao, N., Braid monodromies on proper curves and pro-ℓ Galois representations, J. Inst. Math. Jussieu 11 (2012), 161–181.Google Scholar
Terasoma, T., Relative Deligne cohomologies and higher regulators for Kuga–Sato fiber spaces, Preprint, January 2011.Google Scholar
Tsunogai, H., On some derivations of Lie algebras related to Galois representations, Publ. Res. Inst. Math. Sci. 31 (1995), 113–134.Google Scholar
Voevodsky, V., Suslin, A. and Friedlander, E., Cycles, Transfers, and Motivic Homology Theories, Annals of Mathematics Studies, Volume 143 (Princeton University Press, 2000).Google Scholar
Wasow, W., Asymptotic Expansions for Ordinary Differential Equations, Pure and Applied Mathematics, Volume XIV (Interscience Publishers, 1965).Google Scholar
Zucker, S., Hodge theory with degenerating coefficients, L 2 cohomology in the Poincaré metric, Ann. of Math. (2) 109 (1979), 415–476.Google Scholar