Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-12T01:02:04.752Z Has data issue: false hasContentIssue false
  • English
  • Français

TRUNCATED AFFINE SPRINGER FIBERS AND ARTHUR’S WEIGHTED ORBITAL INTEGRALS

Part of: Discontinuous groups and automorphic forms Special varieties Lie groups

Published online by Cambridge University Press:  10 November 2021

Zongbin Chen Open the ORCID record for Zongbin Chen [Opens in a new window]
Zongbin Chen*
Affiliation:
Yau Mathematical Science Center, Tsinghua University, Jinchunyuan West Building, Office 255, 100084, Haidian District, Beijing, China
*
zbchen@tsinghua.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We explain an algorithm to calculate Arthur’s weighted orbital integral in terms of the number of rational points on the fundamental domain of the associated affine Springer fiber. The strategy is to count the number of rational points of the truncated affine Springer fibers in two ways: by the Arthur–Kottwitz reduction and by the Harder–Narasimhan reduction. A comparison of results obtained from these two approaches gives recurrence relations between the number of rational points on the fundamental domains of the affine Springer fibers and Arthur’s weighted orbital integrals. 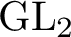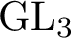As an example, we calculate Arthur’s weighted orbital integrals for the groups ${\textrm {GL}}_{2}$ and ${\textrm {GL}}_{3}$ .

Keywords

Weighted orbital integralsAffine Springer fibersHarder-Narasimhan reductionArthur-Kottwitz reduction

MSC classification

Primary: 22E67: Loop groups and related constructions, group-theoretic treatment 14M15: Grassmannians, Schubert varieties, flag manifolds
Secondary: 11F85: $p$-adic theory, local fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 4 , July 2023 , pp. 1757 - 1818
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arthur, J., The characters of discrete series as orbital integrals, Invent. Math. 32 (1976), 205–261.10.1007/BF01425569CrossRefGoogle Scholar
Arthur, J., The trace formula in invariant form, Ann. of Math. (2) 114 (1981), 1–74.10.2307/1971376CrossRefGoogle Scholar
Arthur, J., A local trace formula, Publ. Math. Inst. Hautes Études Sci. 73 (1991), 5–96.10.1007/BF02699256CrossRefGoogle Scholar
Arthur, J., An introduction to the trace formula , in Harmonic Analysis, the Trace Formula, and Shimura Varieties, Clay Mathematics Proceedings, 4, pp. 1–263 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Bezrukavnikov, R., The dimension of the fixed point set on affine flag manifolds, Math. Res. Lett. 3 (1996), 185–189.10.4310/MRL.1996.v3.n2.a5CrossRefGoogle Scholar
Borovoi, M., Abelian Galois Cohomology of Reductive Groups , Memoirs of the American Mathematical Society, 132(626) (1998).CrossRefGoogle Scholar
Chaudouard, P.-H. and Laumon, G., Sur l’homologie des fibres de Springer affines tronquées, Duke Math. J. 145(3) (2008), 443–535.10.1215/00127094-2008-057CrossRefGoogle Scholar
Chaudouard, P.-H. and Laumon, G., Le lemme fondamental pondéré, I. Constructions géométriques, Compos. Math. 146(6) (2010), 1416–1506.CrossRefGoogle Scholar
Chen, Z., Pureté des fibres de Springer affines pour ${\textrm{GL}}_4$ , Bull. Soc. Math. France 142(2) (2014), 193–222.10.24033/bsmf.2663CrossRefGoogle Scholar
Chen, Z., The $\xi$ -stability on the affine grassmannian, Math. Z. 280(3-4) (2015), 1163–1184.CrossRefGoogle Scholar
Chen, Z., On the fundamental domain of affine Springer fibers, Math. Z. 286(3-4) (2017), 1323–1356.10.1007/s00209-016-1803-xCrossRefGoogle Scholar
Chen, Z., ‘Truncated affine grassmannians and truncated affine Springer fibers for ${\textrm{GL}}_3$ ’, Preprint, (2014), http://arxiv.org/abs/1401.1930.Google Scholar
Goresky, M., Kottwitz, R. and MacPherson, R., Equivariant cohomology, Koszul duality, and the localization theorem. Invent. Math. 131(1) (1998), 25–83.10.1007/s002220050197CrossRefGoogle Scholar
Goresky, M., Kottwitz, R. and MacPherson, R., Homology of affine Springer fibers in the unramified case, Duke Math. J. 121(3) (2004), 509–561.10.1215/S0012-7094-04-12135-9CrossRefGoogle Scholar
Goresky, M., Kottwitz, R. and MacPherson, R., Regular points in affine Springer fibers, Michigan Math. J. 53(1) (2005), 97–107.10.1307/mmj/1114021087CrossRefGoogle Scholar
Goresky, M., Kottwitz, R. and MacPherson, R., Purity of equivalued affine Springer fibers, Represent. Theory 10 (2006), 130–146.10.1090/S1088-4165-06-00200-7CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., Fixed point varieties on affine flag manifolds, Israel. J. Math. 62 (1988), 129–168.10.1007/BF02787119CrossRefGoogle Scholar
Kottwitz, R. E., Isocrystals with additional structure. Compos. Math. 56(2) (1985), 201–220.Google Scholar
Kottwitz, R. E., Isocrystals with additional structure, II, Compos. Math. 109(3) (1997), 255–339.10.1023/A:1000102604688CrossRefGoogle Scholar
Ngô, B. C., Le lemme fondamental pour les algèbres de Lie, Publ. Math. Inst. Hautes Études Sci. 111 (2010), 1–169.CrossRefGoogle Scholar