Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-16T20:27:50.427Z Has data issue: false hasContentIssue false
  • English
  • Français

GAMES AND HEREDITARY BAIRENESS IN HYPERSPACES AND SPACES OF PROBABILITY MEASURES

Part of: Probability theory on algebraic and topological structures Basic constructions Fairly general properties Spaces with richer structures Game theory

Published online by Cambridge University Press:  15 June 2020

Mikołaj Krupski Open the ORCID record for Mikołaj Krupski [Opens in a new window]
Mikołaj Krupski*
Affiliation:
Institute of Mathematics, University of Warsaw, ul. Banacha 2, 02–097Warszawa, Poland (mkrupski@mimuw.edu.pl)
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish that the existence of a winning strategy in certain topological games, closely related to a strong game of Choquet, played in a topological space 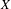$X$ and its hyperspace 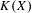$K(X)$ of all nonempty compact subsets of 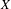$X$ equipped with the Vietoris topology, is equivalent for one of the players. For a separable metrizable space 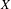$X$, we identify a game-theoretic condition equivalent to 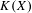$K(X)$ being hereditarily Baire. It implies quite easily a recent result of Gartside, Medini and Zdomskyy that characterizes hereditary Baire property of hyperspaces 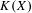$K(X)$ over separable metrizable spaces $X$ via the Menger property of the remainder of a compactification of 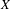$X$. Subsequently, we use topological games to study hereditary Baire property in spaces of probability measures and in hyperspaces over filters on natural numbers. To this end, we introduce a notion of strong $P$-filter 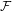${\mathcal{F}}$ and prove that it is equivalent to 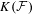$K({\mathcal{F}})$ being hereditarily Baire. We also show that if 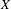$X$ is separable metrizable and 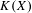$K(X)$ is hereditarily Baire, then the space 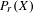$P_{r}(X)$ of Borel probability Radon measures on 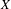$X$ is hereditarily Baire too. It follows that there exists (in ZFC) a separable metrizable space 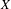$X$, which is not completely metrizable with 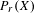$P_{r}(X)$ hereditarily Baire. As far as we know, this is the first example of this kind.

Keywords

hyperspaceVietoris topologyhereditarily Baire spacestrong Choquet gamePorada gameMenger spaceMenger at infinity spacefilterstrong P-filterspace of probability measuresProhorov space

MSC classification

Primary: 54B20: Hyperspaces 54E52: Baire category, Baire spaces 60B05: Probability measures on topological spaces 91A44: Games involving topology or set theory
Secondary: 54D40: Remainders 54D20: Noncompact covering properties (paracompact, Lindelöf, etc.) 54D80: Special constructions of spaces (spaces of ultrafilters, etc.)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 3 , May 2022 , pp. 851 - 868
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aurichi, L. F. and Bella, A., When is a space Menger at infinity? Appl. Gen. Topol. 16 (2015), 75–80.CrossRefGoogle Scholar
Aurichi, L. F. and Dias, R. R., A minicourse on topological games, Topol. Appl. 258 (2019), 305–335.CrossRefGoogle Scholar
Bartoszyński, T. and Tsaban, B., Hereditary topological diagonalizations and the Menger–Hurewicz conjectures, Proc. Amer. Math. Soc. 134 (2006), 605–615.CrossRefGoogle Scholar
Bella, A. and Hernández-Gutiérrez, R., A non-discrete space X with C p(X) Menger at infinity, Appl. Gen. Topol. 20 (2019), 223–230.CrossRefGoogle Scholar
Bella, A., Tokgöz, S. and Zdomskyy, L., Menger remainders of topological groups, Arch. Math. Logic 55 (2016), 767–784.CrossRefGoogle Scholar
Blass, A., Hrušák, M. and Verner, J., On strong P-points, Proc. Amer. Math. Soc. 141 (2013), 2875–2883.CrossRefGoogle Scholar
Bogachev, V. I., Measure Theory. Vol. II (Springer, Berlin, 2007).CrossRefGoogle Scholar
Bouziad, A., A note on consonance of G 𝛿 subsets, Topol. Appl. 87 (1998), 53–61.CrossRefGoogle Scholar
Brown, J. B., Baire category in spaces of probability measures, Fundam. Math. 96 (1977), 189–193.CrossRefGoogle Scholar
Brown, J. B. and Cox, G. V., Baire category in spaces of probability measures. II, Fundam. Math. 121 (1984), 143–148.CrossRefGoogle Scholar
Cao, J., García-Ferreira, S. and Gutev, V., Baire spaces and Vietoris hyperspaces, Proc. Amer. Math. Soc. 135 (2007), 299–303.CrossRefGoogle Scholar
Cao, J. and Tomita, A. H., Baire spaces, Tychonoff powers and the Vietoris topology, Proc. Amer. Math. Soc. 135 (2007), 1565–1573.CrossRefGoogle Scholar
Chaber, J. and Pol, R., On hereditarily Baire spaces, 𝜎-fragmentability of mappings and Namioka property, Topol. Appl. 151 (2005), 132–143.CrossRefGoogle Scholar
Debs, G., Espaces héréditairement de Baire, Fundam. Math. 129 (1988), 199–206.CrossRefGoogle Scholar
Gartside, P., Medini, A. and Zdomskyy, L., The Vietoris hyperspace ${\mathcal{K}}(X)$ is hereditarily Baire if and only if $X$ is co-Menger, preprint, 2018.Google Scholar
Guzmán, O., Hrušák, M. and Martínez-Celis, A., Canjar filters, Notre Dame J. Form. Logic 58 (2017), 79–95.Google Scholar
Henriksen, M. and Isbell, J. R., Some properties of compactifications, Duke Math. J. 25 (1958), 83–105.CrossRefGoogle Scholar
Holá, v. and Pelant, J., Recent progress in hyperspace topologies, in Recent Progress in General Topology, II, pp. 253–285 (North-Holland, Amsterdam, 2002).Google Scholar
Hurewicz, W., Über eine Verallgemeinerung des Borelschen theorems, Math. Z. 24 (1926), 401–421.CrossRefGoogle Scholar
Hurewicz, W., Relativ perfekte Teile von Punktmengen und Mengen (A), Fundam. Math. 12 (1928), 78–109.CrossRefGoogle Scholar
Jordan, F., Consonant spaces and topological games, Topol. Appl. 274 (2020), 107121, 24 pp.CrossRefGoogle Scholar
Kechris, A. S., Classical descriptive set theory, Graduate Texts in Mathematics, Volume 156, (Springer, New York, 1995).CrossRefGoogle Scholar
Laflamme, C., Forcing with filters and complete combinatorics, Ann. Pure Appl. Logic 42 (1989), 125–163.CrossRefGoogle Scholar
Marciszewski, W., P-filters and hereditary Baire function spaces, Topol. Appl. 89 (1998), 241–247.CrossRefGoogle Scholar
McCoy, R. A., Baire spaces and hyperspaces, Pacific J. Math. 58 (1975), 133–142.CrossRefGoogle Scholar
Miller, A. W. and Fremlin, D. H., On some properties of Hurewicz, Menger, and Rothberger, Fundam. Math. 129 (1988), 17–33.CrossRefGoogle Scholar
Porada, E., Jeu de Choquet, Colloq. Math. 42 (1979), 345–353.CrossRefGoogle Scholar
Preiss, D., Metric spaces in which Prohorov’s theorem is not valid, Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 27 (1973), 109–116.CrossRefGoogle Scholar
Scheepers, M., Combinatorics of open covers. I. Ramsey theory, Topol. Appl. 69 (1996), 31–62.CrossRefGoogle Scholar
Telgársky, R., On games of Topsøe, Math. Scand. 54 (1984), 170–176.CrossRefGoogle Scholar
Telgársky, R., Remarks on a game of Choquet, Colloq. Math. 51 (1987), 365–372.CrossRefGoogle Scholar
Topsøe, F., Compactness and tightness in a space of measures with the topology of weak convergence, Math. Scand. 34 (1974), 187–210.CrossRefGoogle Scholar
Tsaban, B. and Zdomskyy, L., Scales, fields, and a problem of Hurewicz, J. Eur. Math. Soc. (JEMS) 10 (2008), 837–866.CrossRefGoogle Scholar
van Douwen, E. K., Closed copies of the rationals, Comment. Math. Univ. Carolin. 28 (1987), 137–139.Google Scholar
Wójcicka, M., Note on the Baire category in spaces of probability measures on nonseparable metrizable spaces, Bull. Polish Acad. Sci. Math. 33 (1985), 305–311.Google Scholar
Wójcicka, M., The space of probability measures on a Prohorov space is Prohorov, Bull. Polish Acad. Sci. Math. 35 (1987), 809–811.Google Scholar