Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhang, Junyong
and
Zheng, Jiqiang
2014.
Scattering theory for nonlinear Schrödinger equations with inverse-square potential.
Journal of Functional Analysis,
Vol. 267,
Issue. 8,
p.
2907.
Bouclet, Jean-Marc
and
Royer, Julien
2015.
Sharp Low Frequency Resolvent Estimates on Asymptotically Conical Manifolds.
Communications in Mathematical Physics,
Vol. 335,
Issue. 2,
p.
809.
Krupchyk, Katsiaryna
and
Uhlmann, Gunther
2015.
On Lp Resolvent Estimates for Elliptic Operators on Compact Manifolds.
Communications in Partial Differential Equations,
Vol. 40,
Issue. 3,
p.
438.
Hassell, Andrew
and
Zhang, Junyong
2016.
Global-in-time Strichartz estimates on nontrapping, asymptotically conic manifolds.
Analysis & PDE,
Vol. 9,
Issue. 1,
p.
151.
Chen, Xi
2018.
Resolvent and spectral measure on non-trapping asymptotically hyperbolic manifolds III: Global-in-time Strichartz estimates without loss.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 35,
Issue. 3,
p.
803.
Huang, Shanlin
Yao, Xiaohua
and
Zheng, Quan
2018.
Remarks on L
p
-limiting absorption principle of Schrödinger operators and applications to spectral multiplier theorems.
Forum Mathematicum,
Vol. 30,
Issue. 1,
p.
43.
Chen, Xi
2018.
Stein–Tomas restriction theorem via spectral measure on metric measure spaces.
Mathematische Zeitschrift,
Vol. 289,
Issue. 3-4,
p.
829.
Bouclet, Jean-Marc
and
Mizutani, Haruya
2018.
Uniform resolvent and Strichartz estimates for Schrödinger equations with critical singularities.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 10,
p.
7293.
Guillarmou, Colin
Hassell, Andrew
and
Krupchyk, Katya
2020.
Eigenvalue bounds for non-self-adjoint
Schrödinger operators with nontrapping metrics.
Analysis & PDE,
Vol. 13,
Issue. 6,
p.
1633.
Sire, Yannick
Sogge, Christopher
Wang, Chengbo
and
Zhang, Junyong
2020.
Strichartz estimates and Strauss conjecture on non-trapping asymptotically hyperbolic manifolds.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 11,
p.
7639.
Gell-Redman, Jesse
Hassell, Andrew
Shapiro, Jacob
and
Zhang, Junyong
2020.
Existence and Asymptotics of Nonlinear Helmholtz Eigenfunctions.
SIAM Journal on Mathematical Analysis,
Vol. 52,
Issue. 6,
p.
6180.
Zhang, Junyong
and
Zheng, Jiqiang
2020.
Strichartz estimates and wave equation in a conic singular space.
Mathematische Annalen,
Vol. 376,
Issue. 1-2,
p.
525.
Mizutani, Haruya
Zhang, Junyong
and
Zheng, Jiqiang
2020.
Uniform resolvent estimates for Schrödinger operator with an inverse-square potential.
Journal of Functional Analysis,
Vol. 278,
Issue. 4,
p.
108350.
Chen, Xi
2022.
The Sobolev inequalities on real hyperbolic
spaces and eigenvalue bounds for Schrödinger operators with complex
potentials.
Analysis & PDE,
Vol. 15,
Issue. 8,
p.
1861.
Zhang, Junyong
2022.
Resolvent and spectral measure for Schrödinger operators on flat Euclidean cones.
Journal of Functional Analysis,
Vol. 282,
Issue. 3,
p.
109311.
Gao, Xiaofen
Yin, Zhiqing
Zhang, Junyong
and
Zheng, Jiqiang
2022.
Decay and Strichartz estimates in critical electromagnetic fields.
Journal of Functional Analysis,
Vol. 282,
Issue. 5,
p.
109350.
Cuenin, Jean-Claude
2024.
From spectral cluster to uniform resolvent estimates on compact manifolds.
Journal of Functional Analysis,
Vol. 286,
Issue. 2,
p.
110214.
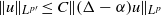 $\Vert u\Vert _{{L}^{p\prime } } \leq C\Vert (\Delta - \alpha )u\Vert _{{L}^{p} } $ for
$\Vert u\Vert _{{L}^{p\prime } } \leq C\Vert (\Delta - \alpha )u\Vert _{{L}^{p} } $ for 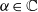 $\alpha \in \mathbb{C} $ and
$\alpha \in \mathbb{C} $ and 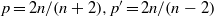 $p= 2n/ (n+ 2), {p}^{\prime } = 2n/ (n- 2)$ on non-trapping asymptotically conic manifolds of dimension
$p= 2n/ (n+ 2), {p}^{\prime } = 2n/ (n- 2)$ on non-trapping asymptotically conic manifolds of dimension 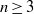 $n\geq 3$, generalizing to non-constant coefficient Laplacians a result of
Kenig, Ruiz and Sogge [13].
$n\geq 3$, generalizing to non-constant coefficient Laplacians a result of
Kenig, Ruiz and Sogge [13].

