Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
McNamara, Peter J.
2012.
Multiple Dirichlet Series, L-functions and Automorphic Forms.
p.
299.
Reich, Ryan
2012.
Twisted geometric Satake equivalence via gerbes on the factorizable grassmannian.
Representation Theory of the American Mathematical Society,
Vol. 16,
Issue. 11,
p.
345.
Brubaker, Benjamin
and
Friedberg, Solomon
2015.
Whittaker Coefficients of Metaplectic Eisenstein Series.
Geometric and Functional Analysis,
Vol. 25,
Issue. 4,
p.
1180.
Lysenko, Sergey
2015.
Twisted Geometric Langlands Correspondence for a Torus.
International Mathematics Research Notices,
Vol. 2015,
Issue. 18,
p.
8680.
Travkin, Roman
2016.
Quantum geometric Langlands correspondence in positive characteristic: The GLN case.
Duke Mathematical Journal,
Vol. 165,
Issue. 7,
Gao, Fan
2017.
Distinguished theta representations for certain covering groups.
Pacific Journal of Mathematics,
Vol. 290,
Issue. 2,
p.
333.
Lysenko, Sergey
2017.
Twisted Whittaker models for metaplectic groups.
Geometric and Functional Analysis,
Vol. 27,
Issue. 2,
p.
289.
Kaplan, Eyal
2017.
THE DOUBLE COVER OF ODD GENERAL SPIN GROUPS, SMALL REPRESENTATIONS, AND APPLICATIONS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 16,
Issue. 3,
p.
609.
Gao, Fan
2018.
Generalized Bump–Hoffstein conjecture for coverings of the general linear groups.
Journal of Algebra,
Vol. 499,
Issue. ,
p.
183.
Lafforgue, Vincent
2018.
Chtoucas pour les groupes réductifs et paramétrisation de Langlands globale.
Journal of the American Mathematical Society,
Vol. 31,
Issue. 3,
p.
719.
Gaitsgory, D.
and
Lysenko, S.
2018.
Parameters and duality for the metaplectic geometric Langlands theory.
Selecta Mathematica,
Vol. 24,
Issue. 1,
p.
227.
Szpruch, Dani
2019.
On Shahidi local coefficients matrix.
manuscripta mathematica,
Vol. 159,
Issue. 1-2,
p.
117.
Cai, Yuanqing
2020.
Unramified Whittaker functions for certain Brylinski–Deligne covering groups.
Forum Mathematicum,
Vol. 32,
Issue. 1,
p.
207.
Zhao, Yifei
2024.
Spectral decomposition of genuine cusp forms over global function fields.
Compositio Mathematica,
Vol. 160,
Issue. 6,
p.
1194.
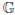 m → E → G(F) → 1; any such extension splits canonically over G(O). Fix a positive integer N and a primitive character ζ : μN(K) →
m → E → G(F) → 1; any such extension splits canonically over G(O). Fix a positive integer N and a primitive character ζ : μN(K) →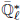 (under some assumption on the characteristic of k). Consider the category of G(O)-bi-invariant perverse sheaves on E with
(under some assumption on the characteristic of k). Consider the category of G(O)-bi-invariant perverse sheaves on E with 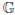 m-monodromy ζ. We show that this is a tensor category, which is tensor equivalent to the category of representations of a reductive group ǦE,N. We compute the root datum of ǦE,N.
m-monodromy ζ. We show that this is a tensor category, which is tensor equivalent to the category of representations of a reductive group ǦE,N. We compute the root datum of ǦE,N.

