No CrossRef data available.
Article contents
SPECTRAL ANALYSIS OF HYPOELLIPTIC RANDOM WALKS
Published online by Cambridge University Press: 08 May 2014
Abstract
We study the spectral theory of a reversible Markov chain This random walk depends on a parameter 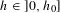 $h\in ]0,h_{0}]$ which is roughly the size of each step of the walk. We prove uniform bounds with respect to
$h\in ]0,h_{0}]$ which is roughly the size of each step of the walk. We prove uniform bounds with respect to 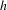 $h$ on the rate of convergence to equilibrium, and the convergence when
$h$ on the rate of convergence to equilibrium, and the convergence when 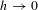 $h\rightarrow 0$ to the associated hypoelliptic diffusion.
$h\rightarrow 0$ to the associated hypoelliptic diffusion.
Keywords
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 3 , July 2015 , pp. 451 - 491
- Copyright
- © Cambridge University Press 2014


