Hostname: page-component-797576ffbb-xg4rj Total loading time: 0 Render date: 2023-12-06T12:19:21.549Z Has data issue: false Feature Flags: { "corePageComponentGetUserInfoFromSharedSession": true, "coreDisableEcommerce": false, "useRatesEcommerce": true } hasContentIssue false
  • English
  • Français

On arithmetic families of filtered 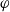$\varphi $-modules and crystalline representations

Part of: Families, fibrations Arithmetic problems. Diophantine geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  19 September 2012

Eugen Hellmann
Eugen Hellmann*
Affiliation:
Mathematisches Institut der Universität Bonn, Endenicher Allee 60, 53115 Bonn, Germany (hellmann@math.uni-bonn.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider stacks of filtered 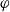$\varphi $-modules over rigid analytic spaces and adic spaces. We show that these modules parameterize 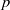$p$-adic Galois representations of the absolute Galois group of a 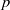$p$-adic field with varying coefficients over an open substack containing all classical points. Further, we study a period morphism (defined by Pappas and Rapoport) from a stack parameterizing integral data, and determine the image of this morphism.

Keywords

Galois representationsp-adic Hodge theory

MSC classification

Secondary: 11F80: Galois representations 11F85: $p$-adic theory, local fields 14D23: Stacks and moduli problems 14G22: Rigid analytic geometry
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 4 , October 2013 , pp. 677 - 726
Copyright
©Cambridge University Press 2012 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berger, L. and Colmez, P., Familles des représentations de de Rham et monodromie $p$-adique, Représentations p-adiques I: représentations Galoisiennes et (φ,Γ)-modules, Asterisque 319 (2008), 303–337.Google Scholar
Berkovich, V., Spectral theory and analytic geometry over non-Archimedian fields, Mathematical Surveys and Monographs, Volume 33 (American Mathematical Society, 1990).Google Scholar
Bosch, S. and Görtz, U., Coherent modules and their descent on relative rigid spaces, J. Reine Angew. Math. 495 (1998), 119–134.Google Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedian Analysis. (Springer-Verlag, Berlin, 1984).Google Scholar
Breuil, C., Groupes $p$-divisibles, groupes finies et modules filtrés, Ann of Math. (2) 152 (2000), 289–549.Google Scholar
Breuil, C., Integral $p$-adic Hodge Theory, in Algebraic Geometry 2000, Azumino, Advanced Studies in Pure Mathematics, Volume 36, pp. 51–80 (Math. Soc. Japan, Tokyo, 2002).Google Scholar
Brinon, O. and Conrad, B., $p$-adic Hodge theory, notes from the CMI summer school, 2009.Google Scholar
Colmez, P. and Fontaine, J.-M., Constructions des représentations $p$-adiques semi-stables, Invent. Math. 140 (2000), 1–43.Google Scholar
Dat, J-F., Orlik, S. and Rapoport, M., Period domains over finite and p-adic fields, Cambridge Tracts in Mathematics, Volume 183 (Cambridge University Press, 2010).Google Scholar
Faltings, G., Coverings of $p$-adic period domains, J. Reine Angew. Math. 643 (2010), 111–139.Google Scholar
Fargues, L. and Fontaine, J.-M., Courbes et fibrés vectoriels en théorie de Hodge $p$-adique, preprint, 2010.Google Scholar
Fontaine, J.-M., Sur certains types des représentations $p$-adiques du groupe d’Galois d’un corps local; construction d’un anneau de Barsotti–Tate, Ann. of Math. (2) 115 (1982), 529–577.Google Scholar
Gruson, L., Fibrés vectoriels sur un polydisque ultramétrique, Ann. Sci. Éc. Norm. Super. (4) 1 (1968), 45–89.Google Scholar
Hartl, U., On a conjecture of Rapoport and Zink, preprint (arXiv:math.NT/0709.3444v3) 2006.Google Scholar
Hartl, U., On period spaces of $p$-divisible groups, C. R. Math. Acad. Sci. Paris, Ser. I 346 (2008), 1123–1128.Google Scholar
Hellmann, E., Weakly admissible filtered $\varphi $-modules and the adjoint quotient of ${\mathrm{GL} }_{d} $, Documenta Math. 16 (2011), 969–991.Google Scholar
Huber, R., Continuous valuations, Math. Z. 212 (1993), 445–447.Google Scholar
Huber, R., A generalization of formal schemes and rigid analytic varieties, Math. Z. 217 (1994), 513–551.Google Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, Volume E30 (Friedr. Vieweg & Sohn, Braunschweig, 1996).Google Scholar
Kedlaya, K., Slope filtrations for relative Frobenius, Représentations p-adiques I: représentations Galoisiennes et (φ,Γ)-modules, Asterisque 319 (2008), 259–301.Google Scholar
Kedlaya, K. and Liu, R., On families of $(\varphi , \Gamma )$-modules, Algebra and Number Theory 4 (7) (2010), 943–967.Google Scholar
Kim, W., The classification of $p$-divisible groups over 2-adic discrete valuation rings, preprint (arXiv:1007.1904) 2010.Google Scholar
Kisin, M., Crystalline representations and $F$-crystals, in Algebraic geometry and number theory, Progress in Mathematics, Volume 253, pp. 459–496 (Birkhäuser Boston, Boston MA, 2006).Google Scholar
Kisin, M., Potentially semi-stable deformation rings, J. Amer. Math. Soc. 21 (2) (2008), 513–546.Google Scholar
Kisin, M., Moduli of finite flat group schemes, and modularity, Ann. of Math. (2) 107 (3) (2009), 1085–1180.Google Scholar
Kisin, M., Modularity of 2-adic Barsotti–Tate representations, Invent. Math. 178 (3) (2009), 587–634.Google Scholar
Lau, E., A relation between Dieudonne displays and crystalline Dieudonne theory, preprint (arXiv:1006.2720) 2010.Google Scholar
Liu, T., The correspondence between Barsotti–Tate groups and Kisin modules when $p= 2$, available at http://41 www.math.purdue.edu/~tongliu/research.html, 1998.Google Scholar
Liu, R., Slope filtrations in families, J. Inst. Math. Jussieu, in press. Available on CJO 2012. doi: 10.1017/S1474748012000709.Google Scholar
Lütkebohmert, W., Vektorraumbündel über nicht archimedischen holomorphen Räumen, Math. Z. 152 (1977), 127–143.Google Scholar
Pappas, G. and Rapoport, M., $\Phi $-modules and coefficient spaces, Moscow Math. J. 9 (3) (2009), 625–664.Google Scholar
Rapoport, M. and Zink, T., Period spaces for p-divisible groups, Annals of Mathematics Studies, Volume 141 (Princeton University Press, Princeton, NJ, 1996).Google Scholar