Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-18T14:32:41.928Z Has data issue: false hasContentIssue false
  • English
  • Français

RIESZ TRANSFORMS AND LITTLEWOOD–PALEY SQUARE FUNCTION ASSOCIATED TO SCHRÖDINGER OPERATORS ON NEW WEIGHTED SPACES

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  18 June 2018

NGUYEN NGOC TRONG  and
LE XUAN TRUONG
NGUYEN NGOC TRONG
Affiliation:
Faculty of Mathematics and Computer Science, VUNHCM – University of Science, Ho Chi Minh city, Vietnam Department of Primary Education, Ho Chi Minh City University of Pedagogy, Ho Chi Minh City, Vietnam email trongnn37@gmail.com
LE XUAN TRUONG*
Affiliation:
University of Economic Ho Chi Minh City, Vietnam email lxuantruong@gmail.com
*
✉lxuantruong@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 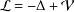${\mathcal{L}}=-\unicode[STIX]{x1D6E5}+{\mathcal{V}}$ be a Schrödinger operator on 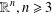$\mathbb{R}^{n},n\geq 3$, where 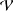${\mathcal{V}}$ is a potential satisfying an appropriate reverse Hölder inequality. In this paper, we prove the boundedness of the Riesz transforms and the Littlewood–Paley square function associated with Schrödinger operators 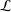${\mathcal{L}}$ in some new function spaces, such as new weighted Bounded Mean Oscillation (BMO) and weighted Lipschitz spaces, associated with 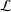${\mathcal{L}}$. Our results extend certain well-known results.

Keywords

Schrödinger operatorRiesz transformsquare functionweighted BMO spaceweighted Lipschitz space

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Secondary: 42B35: Function spaces arising in harmonic analysis
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 105 , Issue 2 , October 2018 , pp. 201 - 228
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Bongioanni, B., Harboure, E. and Salinas, O., ‘Weighted inequalities for negative powers of Schrödinger operators’, J. Math. Anal. Appl. 348 (2008), 12–27.Google Scholar
Bongioanni, B., Harboure, E. and Salinas, O., ‘Riesz transform related to Schrödinger operators acting on BMO type spaces’, J. Math. Anal. Appl. 357 (2009), 115–131.Google Scholar
Bongioanni, B., Harboure, E. and Salinas, O., ‘Classes of weights related to Schrödinger operators’, J. Math. Anal. Appl. 373 (2011), 563–579.Google Scholar
Bui, T. A., ‘The weighted norm inequalities for Riesz transforms of magnetic Schrödinger operators’, Differential Integral Equations 23 (2010), 811–826.Google Scholar
Bui, T. A., ‘Weighted estimates for commutators of some singular integrals related to Schrödinger operators’, Bull. Sci. Math. 138 (2014), 270–292.Google Scholar
Bui, T. A. and Duong, X. T., ‘Boundedness of singular integrals and their commutators with BMO functions on Hardy spaces’, Adv. Differential Equ. 18 (2013), 459–494.Google Scholar
Coulhon, T. and Duong, X. T., ‘Riesz transforms for 1 ≤ p ≤ 2’, Trans. Amer. Math. Soc. 351(3) (1999), 1151–1169.Google Scholar
Duong, X. T., Yan, L. and Zhang, C., ‘On characterization of Poisson integrals of Schrödinger operators with BMO trace’, J. Funct. Anal. 266(4) (2014), 2053–2085.Google Scholar
Dziubański, J., Garrigos, G., Martinez, T., Torrea, J. and Zienkiewicz, J., ‘BMO spaces related to Schrödinger operators with potentials satisfying reverse Hölder inequality’, Math. Z. 249(2) (2005), 329–356.Google Scholar
Dziubański, J. and Zienkiewicz, J., ‘Hardy spaces H 1 associated to Schrödinger operators with potential satisfying reverse Hölder inequality’, Rev. Mat. Iberoam. 15(2) (1999), 279–296.Google Scholar
Dziubański, J. and Zienkiewicz, J., ‘ H p spaces for Schrödinger operators’, Fourier Anal. Relat. Top. 56 (2002), 45–53.Google Scholar
Dziubański, J. and Zienkiewicz, J., ‘ H p spaces associated with Schrödinger operator with potential from reverse Hölder classes’, Colloq. Math. 98(1) (2003), 5–38.Google Scholar
Guo, Z., Li, P. and Peng, L. Z., ‘ L p boundedness of commutators of Riesz transforms associated to Schrödinger operator’, J. Math. Anal. Appl. 341 (2008), 421–432.Google Scholar
Kurata, K., ‘An estimate on the heat kernel of magnetic Schrödinger operators and uniformly elliptic operators with non-negative potentials’, J. Lond. Math. Soc. 62(3) (2000), 885–903.Google Scholar
Liu, H., Tang, L. and Zhu, H., ‘Weighted Hardy spaces and BMO spaces associated with Schrödinger operators’, Math. Nachr. 357 (2012), 1–35.Google Scholar
Morvidone, M., ‘Weighted BMO 𝜙 spaces and the Hilbert transform’, Rev. Un. Mat. Argentina 44 (2003), 1–16.Google Scholar
Muckenhoupt, B. and Wheeden, R. L., ‘Weighted bounded mean oscillation and the Hilbert transform’, Studia Math. 54(3) (1975–1976), 221–237.Google Scholar
Shen, Z., ‘ L p estimates for Schrödinger operators with certain potentials’, Ann. Inst. Fourier 45 (1995), 513–546.Google Scholar
Tang, L., ‘Weighted norm inequalities, spectral multipliers and Littlewood–Paley operators in the Schrödinger settings’, Preprint, 2012, arXiv:1203.0375v1 [math. FA].Google Scholar
Yang, D., Yang, D. and Zhou, Y., ‘Localized BMO and BLO spaces on RD-spaces and applications to Schrödinger operators’, Commun. Pure Appl. Anal. 9 (2010), 779–812.Google Scholar
Yang, D., Yang, D. and Zhou, Y., ‘Localized Morrey–Campanato spaces on metric measure spaces and applications to Schrödinger operators’, Nagoya Math. J. 198 (2010), 77–119.Google Scholar
Yang, D. and Zhou, Y., ‘Localized Hardy spaces H 1 related to admissible functions on RD-spaces and applications to Schrödinger operators’, Trans. Amer. Math. Soc. 363 (2011), 1197–1239.Google Scholar
Zhong, J., ‘Harmonic analysis for some Schrödinger type operators’, PhD Thesis, Princeton University, 1993.Google Scholar