Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-23T16:57:03.125Z Has data issue: false hasContentIssue false
  • English
  • Français

POSITIVE GROUND STATES FOR A CLASS OF SUPERLINEAR 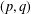$(p,q)$-LAPLACIAN COUPLED SYSTEMS INVOLVING SCHRÖDINGER EQUATIONS

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  29 July 2019

J. C. DE ALBUQUERQUE Open the ORCID record for J. C. DE ALBUQUERQUE [Opens in a new window] ,
JOÃO MARCOS DO Ó Open the ORCID record for JOÃO MARCOS DO Ó [Opens in a new window]  and
EDCARLOS D. SILVA Open the ORCID record for EDCARLOS D. SILVA [Opens in a new window]
J. C. DE ALBUQUERQUE
Affiliation:
Department of Mathematics,Federal University of Pernambuco, 50670-901 Recife – PE, Brazil email joserre@gmail.com, jc@dmat.ufpe.br
JOÃO MARCOS DO Ó
Affiliation:
Department of Mathematics,University of Brasília, 7, 0910-900 Brasília – DF, Brazil email jmbo@pq.cnpq.br
EDCARLOS D. SILVA*
Affiliation:
Institute of Mathematics and Statistics,Federal University of Goiás, 74001-970, Goiás – GO, Brazil email eddomingos@hotmail.com
*
✉eddomingos@hotmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the existence of positive ground state solutions for the following class of 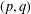$(p,q)$-Laplacian coupled systems

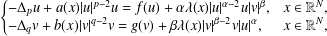$$\begin{eqnarray}\left\{\begin{array}{@{}lr@{}}-\unicode[STIX]{x1D6E5}_{p}u+a(x)|u|^{p-2}u=f(u)+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D706}(x)|u|^{\unicode[STIX]{x1D6FC}-2}u|v|^{\unicode[STIX]{x1D6FD}}, & x\in \mathbb{R}^{N},\\ -\unicode[STIX]{x1D6E5}_{q}v+b(x)|v|^{q-2}v=g(v)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D706}(x)|v|^{\unicode[STIX]{x1D6FD}-2}v|u|^{\unicode[STIX]{x1D6FC}}, & x\in \mathbb{R}^{N},\end{array}\right.\end{eqnarray}$$
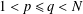where $1<p\leq q<N$. Here the coefficient 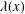$\unicode[STIX]{x1D706}(x)$ of the coupling term is related to the potentials by the condition 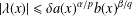$|\unicode[STIX]{x1D706}(x)|\leq \unicode[STIX]{x1D6FF}a(x)^{\unicode[STIX]{x1D6FC}/p}b(x)^{\unicode[STIX]{x1D6FD}/q}$, where 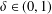$\unicode[STIX]{x1D6FF}\in (0,1)$ and 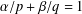$\unicode[STIX]{x1D6FC}/p+\unicode[STIX]{x1D6FD}/q=1$. Using a variational approach based on minimization over the Nehari manifold, we establish the existence of positive ground state solutions for a large class of nonlinear terms and potentials.

Keywords

ground statescoupled systemssuperlinear problemsNehari manifold

MSC classification

Primary: 35J47: Second-order elliptic systems
Secondary: 35J50: Variational methods for elliptic systems 35J92: Quasilinear elliptic equations with $p$-Laplacian
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 2 , October 2020 , pp. 193 - 216
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by INCTmat/MCT/Brazil, CNPq and CAPES/Brazil. The third author was also partially supported by Fapeg/CNpq grants 03/2015-PPP.

References

Akhmediev, N. and Ankiewicz, A., ‘Partially coherent solitons on a finite background’, Phys. Rev. Lett. 82 (1999), 1–4.Google Scholar
Alves, C. O. and Figueiredo, G. M., ‘Existence and multiplicity of positive solutions to a p-Laplacian equation in ℝN’, Differential Integral Equations 19 (2006), 143–162.Google Scholar
Ambrosetti, A. and Colorado, E., ‘Standing waves of some coupled nonlinear Schrödinger equations’, J. Lond. Math. Soc. 75 (2007), 67–82.Google Scholar
Ambrosetti, A. and Rabinowitz, P. H., ‘Dual variational methods in critical point theory and applications’, J. Funct. Anal. 14 (1973), 349–381.Google Scholar
Ambrosetti, A., Cerami, G. and Ruiz, D., ‘Solitons of linearly coupled systems of semilinear non-autonomous equations on ℝN’, J. Funct. Anal. 254 (2008), 2816–2845.10.1016/j.jfa.2007.11.013Google Scholar
Atkinson, C. and Champion, C. R., ‘On some boundary value problems for the equations 𝛻⋅(F (|𝛻u|)𝛻w) = 0’, Proc. R. Soc. Lond. A 448 (1995), 269–279.Google Scholar
Bartsch, T. and Wang, Z. Q., ‘Existence and multiplicity results for some superlinear elliptic problems on ℝN’, Comm. Partial Differential Equations 20 (1995), 1725–1741.Google Scholar
Boccardo, L. and de Figueiredo, D. G., ‘Some remarks on a system of quasilinear elliptic equations’, NoDEA Nonlinear Differential Equations Appl. 9 (2002), 309–323.Google Scholar
Chen, C. and Fu, S., ‘Infinitely many solutions to quasilinear Schrödinger system in ℝN’, Comput. Math. Appl. 71(7) (2016), 1417–1424.Google Scholar
Chen, Z. and Zou, W., ‘On coupled systems of Schrödinger equations’, Adv. Differential Equations 16 (2011), 775–800.Google Scholar
Chen, Z. and Zou, W., ‘Ground states for a system of Schrödinger equations with critical exponent’, J. Funct. Anal. 262 (2012), 3091–3107.Google Scholar
Costa, D. G., ‘On a class of elliptic systems in ℝN’, Electron. J. Differential Equations 7 (1994), 1–14.Google Scholar
Costa, D. G. and Magalhães, C. A., ‘Existence results for perturbations of the p-Laplacian’, Nonlinear Anal. 24 (1995), 409–418.Google Scholar
Díaz, J. I., Nonlinear Partial Differential Equations and Free Boundaries, Vol. I. Elliptic Equations, Research Notes in Mathematics, 106 (Pitman, Boston, 1985).Google Scholar
Dinca, G., Jebelean, P. and Mawhin, J., ‘Variational and topological methods for Dirichlet problems with p-Laplacian’, Port. Math. 58(Fasc. 3) (2001), 339–378.Google Scholar
do Ó, J. M. and de Albuquerque, J. C., ‘Positive ground sate of coupled systems of Schrödinger equations in ℝ2 involving critical exponential growth’, Math. Meth. Appl. Sci. 40 (2017), 6864–6879.Google Scholar
do Ó, J. M. and de Albuquerque, J. C., ‘On coupled systems of nonlinear Schrödinger equations with critical exponential growth’, Appl. Anal. 97(6) (2018), 1000–1015.Google Scholar
do Ó, J. M., de Souza, M. and da Silva, T., ‘On a class quasilinear Schrödinger equations in ℝN’, Appl. Anal. 95 (2016), 323–340.Google Scholar
Drabek, P. and Pohozaev, S. I., ‘Positive solutions for the p-Laplacian: application of the fibering method’, Proc. R. Soc. Edinburgh Sect. A 127 (1997), 703–726.Google Scholar
Esteban, J. R. and Vazquez, J. L., ‘On the equation of turbulent filtration in one dimensional porous media’, Nonlinear Anal. 10 (1986), 1303–1325.Google Scholar
Li, C. and Tang, C.-L., ‘Three solutions for a class of quasilinear elliptic systems involving the (p, q)-Laplacian’, Nonlinear Anal. 69 (2008), 3322–3329.Google Scholar
Li, Q. and Yang, Z., ‘Existence of solutions for a perturbed p-Laplacian system with critical exponent in ℝN’, Appl. Anal. 96(11) (2017), 1885–1905.Google Scholar
Lieberman, G. M., ‘Boundary regularity for solutions of degenerate elliptic equations’, Nonlinear Anal. 12 (1988), 1203–1219.Google Scholar
Lieberman, G. M., ‘The natural generalization of the natural conditions of Ladyzhenskaya and Ural’tseva for elliptic equation’, Comm. Partial Differential Equations 16 (1991), 311–361.Google Scholar
Lions, P. L., ‘The concentration-compactness principle in the calculus of variations. The locally compact case, Part 2’, Ann. Inst. H. Poincaré Anal. Non Linaire 1(4) (1984), 223–283.Google Scholar
Liu, S. B., ‘Existence of solutions to a superlinear p-Laplacian equation’, Electron. J. Differential Equations 66 (2001), 1–6.Google Scholar
Liu, S. B., ‘On ground states of superlinear p-Laplacian equations in ℝN’, J. Math. Anal. Appl. 361 (2010), 48–58.Google Scholar
Maia, L. A. and Silva, E. A. B., ‘On a class of coupled elliptic systems in ℝN’, NoDEA Nonlinear Differential Equations Appl. 14 (2007), 303–313.Google Scholar
Maia, L. A., Montefusco, E. and Pellacci, B., ‘Positive solutions for a weakly coupled nonlinear Schrödinger system’, J. Differ. Equ. 229 (2006), 743–767.Google Scholar
Manouni, S. E. and Touzani, A., ‘On some nonlinear elliptic systems with coercive perturbations in ℝN’, Rev. Mat. Complut. 16(2) (2003), 483–494.Google Scholar
Peral, I., ‘Multiplicity of solutions for the p-Laplacian. Second School of Nonlinear Functional Analysis and Applications to Differential Equations’, Internat. Cent. Theoret. Phys. Trieste (1997), 1–113.Google Scholar
Perera, K. and Tintatev, C., ‘A nodal solution of the scalar field equation at the second minimax level’, Bull. Lond. Math. Soc. 46 (2014), 1218–1225.Google Scholar
Pucci, P. and Serrin, J., ‘The strong maximum principle revisited’, J. Differ. Equ. 196 (2004), 1–66.Google Scholar
Rabinowitz, P., ‘On a class of nonlinear Schrödinger equations’, Z. Angew. Math. Phys. 43 (1992), 270–291.Google Scholar
Stavrakakis, N. M. and Zographopoulos, N. B., ‘Existence results for quasilinear elliptic systems in ℝN’, Electron. J. Differential Equations 39 (1999), 1–15.Google Scholar
Szulkin, A. and Weth, T., ‘Ground state solutions for some indefinite variational problems’, J. Funct. Anal. 257 (2009), 3802–3822.Google Scholar
Szulkin, A. and Weth, T., ‘The method of Nehari manifold’, in: Handbook of Nonconvex Analysis and Applications (International Press, Somerville, MA, 2010), 597–632.Google Scholar
Vélin, J., ‘On an existence result for a class of (p, q)-gradient elliptic systems via a fibering method’, Nonlinear Anal. 75 (2012), 6009–6033.Google Scholar
Vélin, J., ‘Multiple solutions for a class of (p, q)-gradient elliptic systems via a fibering method’, Proc. R. Soc. Edinburgh Sect. A. 144 (2014), 363–393.Google Scholar
Vélin, J. and de Thélin, F., ‘Existence and nonexistence of nontrivial solutions for some nonlinear elliptic systems’, Rev. Mat. Univ. Complut. Madrid 6 (1993), 153–194.Google Scholar
Willem, M., Minimax Theorems (Birkhäser, Boston, 1996).Google Scholar
Wu, T. F., ‘Multiple positive solutions for a class of concave–convex elliptic problems in ℝN involving sign-changing weight’, J. Funct. Anal. 258(1) (2010), 99–131.Google Scholar
Yang, J., ‘Positive solutions of quasilinear elliptic obstacle problems with critical exponents’, Nonlinear Anal. 25 (1995), 1283–1306.Google Scholar
Zhang, G. Q., Liu, X. P. and Liu, S. Y., ‘Remarks on a class of quasilinear elliptic systems involving the (p, q)-Laplacian’, Electron. J. Differential Equations 20 (2005), 1–10.Google Scholar