The ring 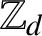$\mathbb Z_{d}$ of d-adic integers has a natural interpretation as the boundary of a rooted d-ary tree 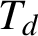$T_{d}$ . Endomorphisms of this tree (that is, solenoidal maps) are in one-to-one correspondence with 1-Lipschitz mappings from 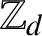$\mathbb Z_{d}$ to itself. In the case when 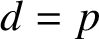$d=p$ is prime, Anashin [‘Automata finiteness criterion in terms of van der Put series of automata functions’,p-Adic Numbers Ultrametric Anal. Appl. 4(2) (2012), 151–160] showed that 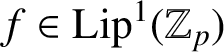$f\in \mathrm {Lip}^{1}(\mathbb Z_{p})$ is defined by a finite Mealy automaton if and only if the reduced coefficients of its van der Put series constitute a p-automatic sequence over a finite subset of 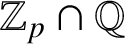$\mathbb Z_{p}\cap \mathbb Q$ . We generalize this result to arbitrary integers 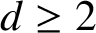$d\geq 2$ and describe the explicit connection between the Moore automaton producing such a sequence and the Mealy automaton inducing the corresponding endomorphism of a rooted tree. We also produce two algorithms converting one automaton to the other and vice versa. As a demonstration, we apply our algorithms to the Thue–Morse sequence and to one of the generators of the lamplighter group acting on the binary rooted tree.