Research Article
Venn-type diagrams for arguments of n terms
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 113-118
-
- Article
- Export citation
Other
Index of reviews
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 429-445
-
- Article
- Export citation
Research Article
Some structure results for propositional calculi1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 271-292
-
- Article
- Export citation
Transcendence of cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-7
-
- Article
- Export citation
A generalization of Nelson's algorithm for obtaining prime implicants
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 8-12
-
- Article
- Export citation
Comments on a variant form of natural deduction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 119-121
-
- Article
- Export citation
Other
Index of reviews by subjects
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 446-480
-
- Article
- Export citation
Research Article
Some consequences of the axiom of power-set
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 293-294
-
- Article
- Export citation
Front matter
JSL volume 30 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Satisfaction for n-th order languages defined in n-th order languages
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 13-25
-
- Article
- Export citation
Analytic natural deduction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 123-139
-
- Article
- Export citation
A formalization of the theory of ordinal numbers1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 295-317
-
- Article
- Export citation
Back matter
JSL volume 30 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Research Article
Interpretations of Kleene's metamathematical predicate Γ ∣ a in intuitionistic arithmetic1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 140-154
-
- Article
- Export citation
Modus ponens under hypotheses
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 26
-
- Article
- Export citation
Metarecursive sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 318-338
-
- Article
- Export citation
An incorrect theorem1
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 27
-
- Article
- Export citation
Some applications of infinitely long formulas
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 339-349
-
- Article
- Export citation
Functionals defined by transfinite recursion
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 155-174
-
- Article
- Export citation
A rudimentary definition of addition
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 350-354
-
- Article
- Export citation

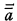 the cardinal of
the cardinal of 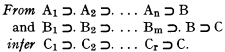
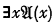 ,
, 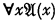 allgemeingültig ist. Die Ausdrücke, die die Identität enthalten, sind dabei eingeschlossen
allgemeingültig ist. Die Ausdrücke, die die Identität enthalten, sind dabei eingeschlossen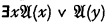 , or from this formula with any other variable in place of
, or from this formula with any other variable in place of 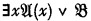 (“Upper formula” in the transitive sense of an upper formula of an upper formula being an upper formula). But then it is stated (incorrectly) that if
(“Upper formula” in the transitive sense of an upper formula of an upper formula being an upper formula). But then it is stated (incorrectly) that if 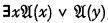 , then
, then 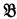 is an upper formula of
is an upper formula of 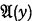 . To show that this is incorrect we here append a proof of the universally valid formula mentioned above:
. To show that this is incorrect we here append a proof of the universally valid formula mentioned above: