Research Article
On first-order sentences without finite models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 329-339
-
- Article
- Export citation
A completeness theorem for symmetric product phase spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 340-370
-
- Article
- Export citation
A universal extender model without large cardinals in V
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 371-386
-
- Article
- Export citation
Implicit proofs
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 387-397
-
- Article
- Export citation
On almost orthogonality in simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 398-408
-
- Article
- Export citation
Bi-isolation in the d.c.e. degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 409-420
-
- Article
- Export citation
A partial analysis of modified realizability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 421-429
-
- Article
- Export citation
Degree spectra of prime models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 430-442
-
- Article
- Export citation
Formalized token models and duality in semantics: an algebraic approach
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 443-477
-
- Article
- Export citation
On a question of Herzog and Rothmaler
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 478-481
-
- Article
- Export citation
Combinatorics for the dominating and unsplitting numbers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 482-498
-
- Article
- Export citation
Semi-bounded relations in ordered modules
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 499-517
-
- Article
- Export citation
Ladder gaps over stationary sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 518-532
-
- Article
- Export citation
Schnorr randomness
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 533-554
-
- Article
- Export citation
Degrees of unsolvability of continuous functions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 555-584
-
- Article
- Export citation
Π11 relations and paths through
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 585-611
-
- Article
- Export citation
An incompleteness theorem for βn-models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 612-616
-
- Article
- Export citation
Front matter
JSL volume 69 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JSL volume 69 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation

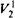 and hence, in particular, polynomially simulates the quantified prepositional calculus
and hence, in particular, polynomially simulates the quantified prepositional calculus 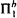 -consequences of
-consequences of 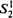 proved with one use of exponentiation. Furthermore, the soundness of
proved with one use of exponentiation. Furthermore, the soundness of 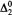 degree
degree 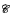 [0,1] computes a non-computable subset of ℕ there is a non-total degree between Turing degrees
[0,1] computes a non-computable subset of ℕ there is a non-total degree between Turing degrees 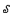 ⊆ 2
⊆ 2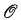
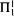 on a structure. We consider some examples of computable structures
on a structure. We consider some examples of computable structures 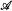 and intrinsically
and intrinsically 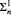 formulas. We prove the following
formulas. We prove the following