Research Article
On Scott and Karp trees of uncountable models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 897-908
-
- Article
- Export citation
The Kunen-Miller chart (Lebesgue measure, the Baire property, Laver reals and preservation theorems for forcing)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 909-927
-
- Article
- Export citation
Weakly minimal groups of unbounded exponent
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 928-937
-
- Article
- Export citation
Partition properties and Prikry forcing on simple spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 938-947
-
- Article
- Export citation
Notions of relative ubiquity for invariant sets of relational structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 948-986
-
- Article
- Export citation
Undecidability and initial segments of the (r.e.) tt-degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 987-1006
-
- Article
- Export citation
Decidable fragments of field theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1007-1018
-
- Article
- Export citation
Partitioning pairs of countable sets of ordinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1019-1021
-
- Article
- Export citation
Set theoretic properties of Loeb measure
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1022-1036
-
- Article
- Export citation
Omitting types for stable ccc theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1037-1047
-
- Article
- Export citation
Maximal r.e. equivalence relations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1048-1058
-
- Article
- Export citation
The interpretability logic of Peano arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1059-1089
-
- Article
- Export citation
Finite Kripke models and predicate logics of provability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1090-1098
-
- Article
- Export citation
Intermediate predicate logics determined by ordinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1099-1124
-
- Article
- Export citation
On the angular component map modulo P
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1125-1129
-
- Article
- Export citation
Coinductive ℵ0-categorical theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1130-1137
-
- Article
- Export citation
Differentially algebraic group chunks
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1138-1142
-
- Article
- Export citation
The axiomatization of randomness
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1143-1167
-
- Article
- Export citation
Effective model theory vs. recursive model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1168-1191
-
- Article
- Export citation
Théories d'algèbres de Boole munies d'idéaux distingués. II
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1192-1212
-
- Article
- Export citation



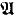 and
and 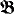 be two countable relational models of the same first order language. If the models are nonisomorphic, there is a unique countable ordinal
be two countable relational models of the same first order language. If the models are nonisomorphic, there is a unique countable ordinal 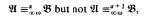
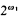 mutually noncomparable Scott trees.
mutually noncomparable Scott trees. of
of 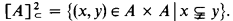
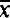 )
)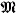 and
and  denote (countable) transitive models of ZFC. cov
denote (countable) transitive models of ZFC. cov 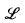 for valued fields. This language
for valued fields. This language 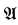 is
is 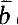 are in k, then a is in the definable closure of k
are in k, then a is in the definable closure of k de
de  composée de l'algèbre de Heyting des idéaux définissables munie de l'opérateur sa et des idéaux distingués, et par l'application qui à tout
composée de l'algèbre de Heyting des idéaux définissables munie de l'opérateur sa et des idéaux distingués, et par l'application qui à tout