Research Article
An abstract Church-Rosser theorem. II: Applications
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-21
-
- Article
- Export citation
Beth definability in infinitary languages
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 22-26
-
- Article
- Export citation
Some remarks on changing cofinalities
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 27-30
-
- Article
- Export citation
Logics containing K4. Part I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 31-42
-
- Article
- Export citation
A result concerning cardinalities of ultraproducts1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 43-48
-
- Article
- Export citation
Least upper bounds for minimal pairs of α-R.E. α-degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 49-56
-
- Article
- Export citation
Sets constructible from sequences of ultrafilters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 57-66
-
- Article
- Export citation
A sequence of decidable finitely axiomatizable intermediate logics with the disjunction property1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 67-78
-
- Article
- Export citation
PCA well-orderings of the line
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 79-80
-
- Article
- Export citation
A formalization of Essenin-Volpin's proof theoretical studies by means of nonstandard analysis
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 81-87
-
- Article
- Export citation
A hierarchy for the 1-section of any type two object
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 88-94
-
- Article
- Export citation
Π10 classes and Boolean combinations of recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 95-96
-
- Article
- Export citation
Index sets in Ershov's hierarchy1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 97-104
-
- Article
- Export citation
Σ1 compactness for next admissible sets1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 105-116
-
- Article
- Export citation
Projective model completeness
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 117-123
-
- Article
- Export citation
Scott's interpolation theorem fails for Lω1, ω
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 124-126
-
- Article
- Export citation
Honest bounds for complexity classes of recursive functions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 127-138
-
- Article
- Export citation
Turing machines and the spectra of first-order formulas
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 139-150
-
- Article
- Export citation
On certain types and models for arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 151-162
-
- Article
- Export citation
A new proof that analytic sets are Ramsey
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 163-165
-
- Article
- Export citation



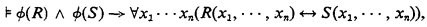
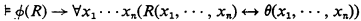
 over a set
over a set  ? Although many special results are known, several problems remain open (see [5] for a survey). For example, consider a uniform ultrafilter
? Although many special results are known, several problems remain open (see [5] for a survey). For example, consider a uniform ultrafilter 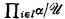 has power
has power 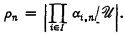
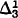 well-ordering of the reals. In addition we generalize a result of Kunen to characterize the countaby complete ultrafilters of
well-ordering of the reals. In addition we generalize a result of Kunen to characterize the countaby complete ultrafilters of 
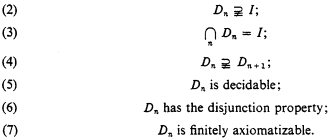
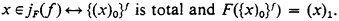
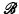 be the collection of all sets which are finite Boolean combinations of recursively enumerable (r.e.) sets of numbers. Dale Myers asked [private correspondence] whether there exists a nonempty
be the collection of all sets which are finite Boolean combinations of recursively enumerable (r.e.) sets of numbers. Dale Myers asked [private correspondence] whether there exists a nonempty 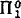 class of sets containing no member of
class of sets containing no member of 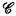 be a class of subsets of
be a class of subsets of 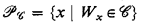 be the set of indices of recursively enumerable sets
be the set of indices of recursively enumerable sets 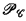
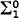 complete set. This theorem will be partially extended to classes which are boolean combinations of open sets by the following:
complete set. This theorem will be partially extended to classes which are boolean combinations of open sets by the following: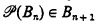 for each
for each 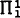 reflection [2]. While his characterization has been of interest in understanding the Σ
reflection [2]. While his characterization has been of interest in understanding the Σ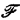 -sentence C such that A → C and C → B iff whenever
-sentence C such that A → C and C → B iff whenever 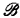 and
and 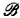 are
are 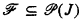 define an
define an 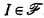 , i.e., a sentence consisting of
, i.e., a sentence consisting of 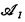 , be the structure obtained by restricting
, be the structure obtained by restricting 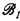 for each
for each 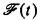 be the set of recursive functions computable by machines using at most
be the set of recursive functions computable by machines using at most 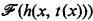 . This turns out not to be the case: The “gap theorem” ([2], [3]) implies that for every recursive
. This turns out not to be the case: The “gap theorem” ([2], [3]) implies that for every recursive 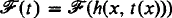 . However, if we restrict our attention to names from a certain subclass of the recursive functions, then we can indeed uniformly increase the size of our
. However, if we restrict our attention to names from a certain subclass of the recursive functions, then we can indeed uniformly increase the size of our 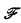 -classes. Informally, we call a recursive function
-classes. Informally, we call a recursive function 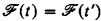 .
.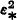 and are properly included in
and are properly included in 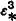 . However, no progress has been made toward establishing whether spectra properly include
. However, no progress has been made toward establishing whether spectra properly include