Research Article
The complexity of ODDnA
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-18
-
- Article
- Export citation
The distribution of properly Σ20 e-degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 19-32
-
- Article
- Export citation
The anatytic conception of truth and the foundations of arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 33-102
-
- Article
- Export citation
Pure-projective modules and positive constructibility
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 103-110
-
- Article
- Export citation
Trois theoremes sur l'induction pour les formules ouvertes munies de l'exponentielle
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 111-154
-
- Article
- Export citation
Vaught's conjecture for modules over a serial ring
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 155-163
-
- Article
- Export citation
Recursive in a generic real
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 164-172
-
- Article
- Export citation
A non-standard construction of Haar measure and weak König's lemma
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 173-186
-
- Article
- Export citation
A finite basis theorem for residually finite, congruence meet-semidistributive varieties
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 187-200
-
- Article
- Export citation
An extension of the Cobham-Semënov Theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 201-211
-
- Article
- Export citation
Property theory and the revision theory of definitions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 212-246
-
- Article
- Export citation
Separating stationary reflection principles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 247-258
-
- Article
- Export citation
Filters, Cohen sets and consistent extensions of the Erdős-Dushnik-Miller Theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 259-271
-
- Article
- Export citation
On inverse γ-systems and the number of L∞λ-equivalent, non-isomorphic models for λ singular
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 272-284
-
- Article
- Export citation
Structural properties and Σ20 enumeration degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 285-292
-
- Article
- Export citation
Coordinatisation and canonical bases in simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 293-309
-
- Article
- Export citation
Logical questions concerning the μ-calculus: Interpolation, Lyndon and Łoś-Tarski
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 310-332
-
- Article
- Export citation
Two consistency results on set mappings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 333-338
-
- Article
- Export citation
The liar paradox and fuzzy logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 339-346
-
- Article
- Export citation
Some applications of ordinal dimensions to the theory of differentially closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 347-356
-
- Article
- Export citation



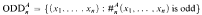
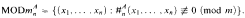
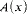 with
with 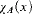 , where χ
, where χ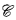 contained in the set of 1-generic reals and a first order structure
contained in the set of 1-generic reals and a first order structure 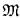 such that for any real number
such that for any real number 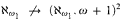 and consistently,
and consistently, 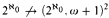 .
.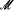 of cardinality λ, let No(
of cardinality λ, let No(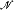 of cardinality λ which are
of cardinality λ which are 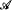 of abelian groups and their certain kind of quotient limits Gr(
of abelian groups and their certain kind of quotient limits Gr(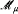 , of cardinality λ with No(
, of cardinality λ with No(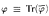 for all sentences φ? This problem is investigated in the frame of Łukasiewicz infinitely valued logic.
for all sentences φ? This problem is investigated in the frame of Łukasiewicz infinitely valued logic.