Research Article
Gentzenizations of relevant logics without distribution. I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 353-378
-
- Article
- Export citation
Gentzenizations of relevant logics without distribution. II
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 379-401
-
- Article
- Export citation
Gentzenizations of relevant logics with distribution
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 402-420
-
- Article
- Export citation
Canonical formulas for K4. Part II: Cofinal subframe logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 421-449
-
- Article
- Export citation
The Sacks density theorem and Σ2-bounding
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 450-467
-
- Article
- Export citation
On power set in explicit mathematics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 468-489
-
- Article
- Export citation
Set theoretic naturalism
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 490-514
-
- Article
- Export citation
Definability and decidability issues in extensions of the integers with the divisibility predicate
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 515-540
-
- Article
- Export citation
The undecidability of second order linear logic without exponentials
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 541-548
-
- Article
- Export citation
On finite rigid structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 549-562
-
- Article
- Export citation
Stretchings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 563-585
-
- Article
- Export citation
On external Scott algebras in nonstandard models of Peano arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 586-607
-
- Article
- Export citation
Fluted formulas and the limits of decidability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 608-620
-
- Article
- Export citation
Fine structure for tame inner models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 621-639
-
- Article
- Export citation
Automorphism–invariant measures on ℵ0-categorical structures without the independence property
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 640-652
-
- Article
- Export citation
Did Tarski commit “Tarski's fallacy”?
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 653-686
-
- Article
- Export citation
Reviews
Alexandre Borovik and Ali Nesin. Groups of finite Morley rank. Oxford logic guides, no. 26. Clarendon Press, Oxford University Press, Oxford and New York1994, xvii + 409 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 687-688
-
- Article
- Export citation
Richard Dedekind. What are numbers and what should they be? (Was sind und was sollen die Zahlen?) Revised English translation of 70½ 1 with added notes by H. Pogorzelski, W. Ryan, and W. Snyder. RIM monographs in mathematics. Research Institute for Mathematics, Orono, Maine, 1995, viii + 91 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 688-689
-
- Article
- Export citation
Wolfgang Carl. Frege's theory of sense and reference. Its origins and scope. Modern European philosophy. Cambridge University Press, Cambridge, Neuyork, und Oakleigh, Victoria, 1994, viii + 220 S.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 689-691
-
- Article
- Export citation
Truth or consequences, Essays in honor of Nuel Belnap, edited by J. Michael Dunn and Anil Gupta, Kluwer Academic Publishers, Dordrecht, Boston, and London, 1990, xii + 378 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 691-693
-
- Article
- Export citation

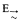 and proved its decidability, though their Gentzenization employed commas on both sides of the turnstile. Subsequently, in 1966, the logic R without distribution, now called LR (for lattice R), was Gentzenized in a similar style by Meyer in [20]. He also went on to show decidability for LR by extending Kripke's argument. Later, in 1969, Dunn Gentzenized R
and proved its decidability, though their Gentzenization employed commas on both sides of the turnstile. Subsequently, in 1966, the logic R without distribution, now called LR (for lattice R), was Gentzenized in a similar style by Meyer in [20]. He also went on to show decidability for LR by extending Kripke's argument. Later, in 1969, Dunn Gentzenized R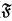 and every set
and every set 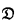 of antichains (which were called
of antichains (which were called 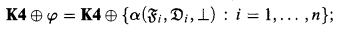
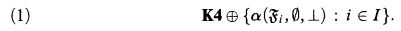
 . As was shown in Part I, almost all standard modal logics are in
. As was shown in Part I, almost all standard modal logics are in  be a first-order structure; we denote by DEF(
be a first-order structure; we denote by DEF(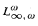 formula with counting quantifiers defines a linear order.
formula with counting quantifiers defines a linear order.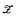 of sets of integers to be equal to the algebra of all sets of integers definable in a nonstandard elementary extension of
of sets of integers to be equal to the algebra of all sets of integers definable in a nonstandard elementary extension of 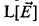 models all of whose levels are tame (defined in [St2] and below). As a consequence, more powerful large cardinal properties reflect to fine structural inner models. For example, we get the following extension to [MiSt, Theorem 11.3] and [St2, Theorem 0.3].
models all of whose levels are tame (defined in [St2] and below). As a consequence, more powerful large cardinal properties reflect to fine structural inner models. For example, we get the following extension to [MiSt, Theorem 11.3] and [St2, Theorem 0.3].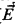 such that
such that