Other
Related Citations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 348-356
-
- Article
- Export citation
Notice of a meeting of the Association for Symbolic Logic
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 356
-
- Article
- Export citation
Research Article
Some theorems on R-maximal sets and major subsets of recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 193-215
-
- Article
- Export citation
Infinitary analogs of theorems from first order model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 216-228
-
- Article
- Export citation
Decision problems for tag systems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 229-239
-
- Article
- Export citation
On theories categorical in their own power
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 240-244
-
- Article
- Export citation
On effectively discontinuous type-2 objects
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 245-248
-
- Article
- Export citation
A logic stronger than intuitionism1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 249-261
-
- Article
- Export citation
Two interpolation theorems for a
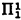 predicate calculus1
predicate calculus1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 262-270
-
- Article
- Export citation
Recursively enumerable sets which are uniform for finite extensions1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 271-287
-
- Article
- Export citation
Natural well-orderings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 288-300
-
- Article
- Export citation
Some contrasts between degrees and the arithmetical hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 301-304
-
- Article
- Export citation
On large cardinals and partition relations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 305-308
-
- Article
- Export citation
Can there be no nonrecursive functions?
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 309-315
-
- Article
- Export citation
Reviews
Reviews - L. Jonathan Cohen. The diversity of meaning. Methuen & Co. Ltd, London1962, and Herder and Herder, New York 1963, xi + 340 pp.; also second edition, Methuen & Co. Ltd, London 1966, xii + 369 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 316-318
-
- Article
- Export citation
Isaac Levi. Gambling with truth. An essay on induction and the aims of science. Alfred A. Knopf, New York, and Routledge & Kegan Paul, Ltd., London, 1967, xiv + 246 + v pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 318-320
-
- Article
- Export citation
Jerrold J. Katz. The problem of induction and its solution. The University of Chicago Press, Chicago1962, xiii + 125 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 320
-
- Article
- Export citation
Rudolf Carnap. On the use of Hilbert's ε-operator in scientific theories. Essays on the foundations of mathematics, dedicated to A. A. Fraenkel on his seventieth anniversary, edited by Y. Bar-Hillel, E. I. J. Poznanski, M. O. Rabin, and A. Robinson for The Hebrew University of Jerusalem, Magnes Press, Jerusalem 1961, and North-Holland Publishing Company, Amsterdam1962, pp. 156–164.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 320-321
-
- Article
- Export citation
William W. Rozeboom. Of selection operators and semanticists. Philosophy of science vol. 31 (1964), pp. 282–285.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 321
-
- Article
- Export citation
David Lewis. How to define theoretical terms. The journal of philosophy, vol. 67 (1970), pp. 427–446.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 321
-
- Article
- Export citation

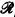 /
/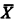 denote the complement of
denote the complement of 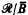 are elementarily equivalent (
are elementarily equivalent (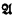
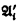 , have the same true
, have the same true 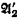 have the same true
have the same true  ), partial recursive in
), partial recursive in 
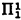 predicate calculus
predicate calculus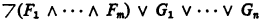
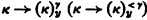 the partition relation
the partition relation 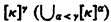
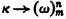 for each
for each  set of integers.
set of integers.