In recent years, much work in descriptive set theory has been focused on the Borel complexity of naturally occurring classification problems, in particular, the study of countable Borel equivalence relations and their structure under the quasi-order of Borel reducibility. Following the approach of Louveau and Rosendal for the study of analytic equivalence relations, we study countable Borel quasi-orders.

In this paper we are concerned with universal countable Borel quasi-orders, i.e., countable Borel quasi-orders above all other countable Borel quasi-orders with regard to Borel reducibility. We first establish that there is a universal countable Borel quasi-order, and then establish that several countable Borel quasi-orders are universal. An important example is an embeddability relation on descriptive set theoretic trees.

Our main result states that embeddability of finitely generated groups is a universal countable Borel quasi-order, answering a question of Louveau and Rosendal. This immediately implies that biembeddability of finitely generated groups is a universal countable Borel equivalence relation. The same techniques are also used to show that embeddability of countable groups is a universal analytic quasi-order.

Finally, we show that, up to Borel bireducibility, there are 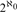${2^{{\aleph _0}}}$ distinct countable Borel quasi-orders, which symmetrize to a universal countable Borel equivalence relation.