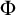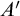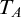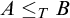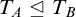Keisler’s order (Definition 1.1) is a pre-order on complete countable first-order theories introduced by Keisler in 1967 [Reference Keisler6], often thought of as a partial order on the equivalence classes. Informally, this order puts
![]() $T_1 \trianglelefteq T_2$
if it is “harder” for the regular ultrapowers of
$T_1 \trianglelefteq T_2$
if it is “harder” for the regular ultrapowers of
![]() $T_2$
to be saturated than those of
$T_2$
to be saturated than those of
![]() $T_1$
. Sorting out the structure of this order has long been an important test problem for model theory. For orientation, we note the following. A minimum class and a maximum class exist [Reference Keisler6]. The union of the smallest two classes is precisely the stable theories [Reference Shelah13]. The maximum class includes clearly complicated theories like Peano arithmetic [Reference Keisler6], but also any theory with linear order (with the strict order property) [Reference Shelah13], and indeed with
$T_1$
. Sorting out the structure of this order has long been an important test problem for model theory. For orientation, we note the following. A minimum class and a maximum class exist [Reference Keisler6]. The union of the smallest two classes is precisely the stable theories [Reference Shelah13]. The maximum class includes clearly complicated theories like Peano arithmetic [Reference Keisler6], but also any theory with linear order (with the strict order property) [Reference Shelah13], and indeed with
![]() $\operatorname {SOP_2}$
[Reference Malliaris and Shelah9]. In between, no classes have yet been characterized, but we know that the random graph is in the minimum unstable class [Reference Malliaris8, Reference Malliaris and Shelah10].
$\operatorname {SOP_2}$
[Reference Malliaris and Shelah9]. In between, no classes have yet been characterized, but we know that the random graph is in the minimum unstable class [Reference Malliaris8, Reference Malliaris and Shelah10].
A recent breakthrough in [Reference Malliaris and Shelah11] has shown that Keisler’s order has the maximum number of classes, continuum many, and that this is already witnessed by theories which look like “filtered random graphs”—indeed, so-called simple unstable rank 1 theories. Recall that by [Reference Shelah13], all NIP theories (informally, those without any randomness) fall into three classes. The recent work shows that near the random graph, things are very different, due in part to interactions of model theory and finite combinatorics (see [Reference Malliaris and Shelah11, Section 3]). Indeed, [Reference Malliaris and Shelah11, Section 12] shows that Keisler’s order embeds
![]() $\mathcal {P}(\omega )/\operatorname {fin}$
, in this region. At this point it was natural to ask (as was recorded in [Reference Malliaris and Shelah11, 13.7], and noticed by readers of that paper, who encouraged us) whether Keisler’s order embeds the “gold standard” for complexity, the Turing degrees.
$\mathcal {P}(\omega )/\operatorname {fin}$
, in this region. At this point it was natural to ask (as was recorded in [Reference Malliaris and Shelah11, 13.7], and noticed by readers of that paper, who encouraged us) whether Keisler’s order embeds the “gold standard” for complexity, the Turing degrees.
The aim of this paper is to answer this question positively, hopefully as groundwork for future theorems. First we give an embedding, with no information about complexity, of an arbitrary partial order with the countable predecessor property into Keisler’s order (Theorem 1.2). Then we show that in the case of the Turing degrees the complexity can be meaningfully calibrated: Theorem 3.11 shows that there is a Turing machine
![]() $\Phi $
, which on input
$\Phi $
, which on input
![]() $A^\prime $
produces a theory
$A^\prime $
produces a theory
![]() $T_A$
, which is uniform in the jump and degree invariant, and which has the property that
$T_A$
, which is uniform in the jump and degree invariant, and which has the property that
![]() $A \leq _T B$
if and only if
$A \leq _T B$
if and only if
![]() $T_A \trianglelefteq T_B$
in Keisler’s order. As will be discussed below, this can be seen as a best possible effective version of Theorem 1.2 on the Turing degrees. In the last section, we show (surprisingly) that for related theories we may stay at the level of the complexity of A, avoiding the jump.
$T_A \trianglelefteq T_B$
in Keisler’s order. As will be discussed below, this can be seen as a best possible effective version of Theorem 1.2 on the Turing degrees. In the last section, we show (surprisingly) that for related theories we may stay at the level of the complexity of A, avoiding the jump.
Are there substantive connections between the structure of Turing degrees and classes of simple unstable theories? We do not assert this, but a priori, it may seem no less likely than the connections to cardinal invariants of the continuum [Reference Malliaris and Shelah9].
We are very grateful to D. Hirschfeldt, I. Scott, and the anonymous referee for comments and questions which significantly improved the presentation, and encouraging us to solve the problem of avoiding the jump.
1 A baseline proof
Definition 1.1 (Keisler’s order [Reference Keisler6])
Let
![]() $T_1, T_2$
be complete countable first-order theories. We say
$T_1, T_2$
be complete countable first-order theories. We say
![]() $T_1 \trianglelefteq T_2$
if for every infinite
$T_1 \trianglelefteq T_2$
if for every infinite
![]() $\lambda $
, every regular ultrafilter
$\lambda $
, every regular ultrafilter
![]() $\mathcal {D}$
on
$\mathcal {D}$
on
![]() $\lambda $
, every model
$\lambda $
, every model
![]() $M_1 \models T_1$
, and every model
$M_1 \models T_1$
, and every model
![]() $M_2 \models T_2$
, if
$M_2 \models T_2$
, if
![]() $(M_2)^\lambda /\mathcal {D}$
is
$(M_2)^\lambda /\mathcal {D}$
is
![]() $\lambda ^+$
-saturated, then
$\lambda ^+$
-saturated, then
![]() $(M_1)^\lambda /\mathcal {D}$
is
$(M_1)^\lambda /\mathcal {D}$
is
![]() $\lambda ^+$
-saturated.
$\lambda ^+$
-saturated.
Regular ultrafilters are easy to find (all nonprincipal ultrafilters on
![]() $\omega $
are regular; consistently all ultrafilters are regular; see [Reference Chang and Keisler3, Chapter 3]). Their significance here is that they make Keisler’s order about theories, not models, since by a lemma of Keisler, if
$\omega $
are regular; consistently all ultrafilters are regular; see [Reference Chang and Keisler3, Chapter 3]). Their significance here is that they make Keisler’s order about theories, not models, since by a lemma of Keisler, if
![]() $M \equiv N$
in a countable language and
$M \equiv N$
in a countable language and
![]() $\mathcal {D}$
is a regular ultrafilter on
$\mathcal {D}$
is a regular ultrafilter on
![]() $\lambda $
, then either both
$\lambda $
, then either both
![]() $M^\lambda /\mathcal {D}$
and
$M^\lambda /\mathcal {D}$
and
![]() $N^\lambda /\mathcal {D}$
are
$N^\lambda /\mathcal {D}$
are
![]() $\lambda ^+$
-saturated, or neither is. See [Reference Keisler6, 2.1a]. For more on Keisler’s order, see, e.g., [Reference Keisler6], [Reference Shelah13, Chapter VI], [Reference Malliaris7, Chapter 1], [Reference Malliaris and Shelah10, Section 1], or [Reference Casey and Malliaris2, Sections 2 and 3].
$\lambda ^+$
-saturated, or neither is. See [Reference Keisler6, 2.1a]. For more on Keisler’s order, see, e.g., [Reference Keisler6], [Reference Shelah13, Chapter VI], [Reference Malliaris7, Chapter 1], [Reference Malliaris and Shelah10, Section 1], or [Reference Casey and Malliaris2, Sections 2 and 3].
For our first proof, we will need the following theorem of [Reference Malliaris and Shelah11], which establishes the surprising fact that Keisler’s order has continuum many classes. (For orientation, note that up to renaming of symbols in the language, there are really only continuum many complete countable theories, and of course each class must contain at least one theory; so there could not be more than continuum many classes.)
Theorem A (see Theorem 11.3 of [Reference Malliaris and Shelah11])
There exist continuum many complete countable simple theories
![]() $\langle T_\alpha : \alpha < 2^{\aleph _0} \rangle $
such that for any countable
$\langle T_\alpha : \alpha < 2^{\aleph _0} \rangle $
such that for any countable
![]() $u, v \subseteq 2^{\aleph _0}$
,
$u, v \subseteq 2^{\aleph _0}$
,
![]() $T_u \trianglelefteq T_v$
if and only if
$T_u \trianglelefteq T_v$
if and only if
![]() $u \subseteq v$
, where
$u \subseteq v$
, where
![]() $T_u$
denotes the disjoint union of the theories
$T_u$
denotes the disjoint union of the theories
![]() $\{ T_\alpha : \alpha \in u \}$
, and similarly for
$\{ T_\alpha : \alpha \in u \}$
, and similarly for
![]() $T_v$
.
$T_v$
.
From Theorem A we may now easily derive:
Theorem 1.2. Let
![]() $(\mathcal {T}, \leq )$
be a partial order which satisfies:
$(\mathcal {T}, \leq )$
be a partial order which satisfies:
-
(1)
 $|\mathcal {T}| \leq 2^{\aleph _0}$
,
$|\mathcal {T}| \leq 2^{\aleph _0}$
, -
(2) for every
 $\mathfrak {b} \in \mathcal {T}$
, the set
$\mathfrak {b} \in \mathcal {T}$
, the set
 $\{ \mathfrak {a} \in \mathcal {T} : \mathfrak {a} \leq \mathfrak {b} \}$
is at most countable.
$\{ \mathfrak {a} \in \mathcal {T} : \mathfrak {a} \leq \mathfrak {b} \}$
is at most countable.
Then
![]() $(\mathcal {T}, \leq )$
embeds in Keisler’s order. That is, there is a map f from
$(\mathcal {T}, \leq )$
embeds in Keisler’s order. That is, there is a map f from
![]() $\mathcal {T}$
to the set of complete countable first order theories such that for any two
$\mathcal {T}$
to the set of complete countable first order theories such that for any two
![]() $\mathfrak {a}, \mathfrak {b} \in \mathcal {T}$
,
$\mathfrak {a}, \mathfrak {b} \in \mathcal {T}$
,
![]() $\mathfrak {a} \leq \mathfrak {b}$
in
$\mathfrak {a} \leq \mathfrak {b}$
in
![]() $\mathcal {T}$
if and only if
$\mathcal {T}$
if and only if
![]() $f(\mathfrak {a}) \trianglelefteq f(\mathfrak {b})$
.
$f(\mathfrak {a}) \trianglelefteq f(\mathfrak {b})$
.
Proof Start with the family of theories from Theorem A above. Fix an injection g from
![]() $\mathcal {T}$
to this family, notation
$\mathcal {T}$
to this family, notation
![]() $\mathfrak {a} \mapsto T_{\alpha (\mathfrak {a})}$
, possible by condition (1). Note that any two elements in the range of g are
$\mathfrak {a} \mapsto T_{\alpha (\mathfrak {a})}$
, possible by condition (1). Note that any two elements in the range of g are
![]() $\trianglelefteq $
-incomparable. Now define
$\trianglelefteq $
-incomparable. Now define
![]() $T_{\mathfrak {a}}$
to be the disjoint union of
$T_{\mathfrak {a}}$
to be the disjoint union of
![]() $\{ T_{\alpha (\mathfrak {b})} : \mathfrak {b} \leq \mathfrak {a} \}$
. This remains a countable theory by condition (2). By construction,
$\{ T_{\alpha (\mathfrak {b})} : \mathfrak {b} \leq \mathfrak {a} \}$
. This remains a countable theory by condition (2). By construction,
![]() $\mathfrak {b} \leq \mathfrak {a}$
if and only if
$\mathfrak {b} \leq \mathfrak {a}$
if and only if
![]() $T_{\mathfrak {b}} \trianglelefteq T_{\mathfrak {a}}$
.
$T_{\mathfrak {b}} \trianglelefteq T_{\mathfrak {a}}$
.
Conclusion 1.3. There is an embedding of the partial order of Turing degrees into Keisler’s order.
Proof The Turing degrees as a partial order satisfy the hypotheses of Theorem 1.2.
Observe that Theorem 1.2 (or Conclusion 1.3) tells us nothing a priori about the complexity of the embedding f. It is natural to hope that restricting the embedding to the Turing degrees, which come equipped with natural notions of complexity, it may be possible to determine the complexity of the map in a meaningful way.
2 Discussion
One reason to hope for more than Conclusion 1.3 on the Turing degrees is that the theories
![]() $T_\alpha $
in Theorem A are themselves parametrized by subsets of
$T_\alpha $
in Theorem A are themselves parametrized by subsets of
![]() $\omega $
. Briefly, each theory involves two key ingredients: a fast-growing sequence of sparse finite graphs
$\omega $
. Briefly, each theory involves two key ingredients: a fast-growing sequence of sparse finite graphs
![]() $\bar {E} = \langle E_n : n < \omega \rangle $
, and a subset
$\bar {E} = \langle E_n : n < \omega \rangle $
, and a subset
![]() $A \subseteq \omega $
. The set A represents the “active levels”
$A \subseteq \omega $
. The set A represents the “active levels”
![]() $n \in \omega $
where constraints coming from
$n \in \omega $
where constraints coming from
![]() $E_n$
apply; at “lazy levels”
$E_n$
apply; at “lazy levels”
![]() $n \in \omega \setminus A$
,
$n \in \omega \setminus A$
,
![]() $E_n$
is replaced by a complete graph on the same set of vertices, which corresponds to no constraints. (In [Reference Malliaris and Shelah11], instead of a set A we often write its characteristic function
$E_n$
is replaced by a complete graph on the same set of vertices, which corresponds to no constraints. (In [Reference Malliaris and Shelah11], instead of a set A we often write its characteristic function
![]() $\xi $
, and there we list separately the sequence
$\xi $
, and there we list separately the sequence
![]() $\bar {m}$
of integers giving the sizes of the vertex sets of the E’s.) The data of
$\bar {m}$
of integers giving the sizes of the vertex sets of the E’s.) The data of
![]() $\bar {E}$
and A (or
$\bar {E}$
and A (or
![]() $\xi $
), and implicitly
$\xi $
), and implicitly
![]() $\bar {m}$
, are part of a “parameter,” denoted by
$\bar {m}$
, are part of a “parameter,” denoted by
![]() $\mathfrak {m}$
, which then determines a theory
$\mathfrak {m}$
, which then determines a theory
![]() $T_{\mathfrak {m}}$
. In [Reference Malliaris and Shelah11], we used a fixed sequence
$T_{\mathfrak {m}}$
. In [Reference Malliaris and Shelah11], we used a fixed sequence
![]() $\bar {E}$
and continuum many sets A which were “suitably independent” (in the sense of Engelking–Kar[Reference Engelking and Karłowicz4]; see [Reference Malliaris and Shelah11, 6.20–6.22]) to produce the many different theories. This is a compact way of simulating many independent growth rates of graph sequences. So we can consider the parameters (thus, the theories) as given by certain subsets of
$\bar {E}$
and continuum many sets A which were “suitably independent” (in the sense of Engelking–Kar[Reference Engelking and Karłowicz4]; see [Reference Malliaris and Shelah11, 6.20–6.22]) to produce the many different theories. This is a compact way of simulating many independent growth rates of graph sequences. So we can consider the parameters (thus, the theories) as given by certain subsets of
![]() $\omega $
.
$\omega $
.
Convention 2.4. For the rest of the paper, we fix a sequence of graphs
![]() $\bar {E}$
as in [Reference Malliaris and Shelah11, Section 6], so a parameter in the sense of [Reference Malliaris and Shelah11] is specified by the additional data of the set of active levels, and it makes sense to write “
$\bar {E}$
as in [Reference Malliaris and Shelah11, Section 6], so a parameter in the sense of [Reference Malliaris and Shelah11] is specified by the additional data of the set of active levels, and it makes sense to write “
![]() $\mathfrak {m}[A]$
” and “
$\mathfrak {m}[A]$
” and “
![]() $T_{\mathfrak {m}[A]}$
.”
$T_{\mathfrak {m}[A]}$
.”
However, consider the following theorem.Footnote 1
Theorem B (Translation of [Reference Malliaris and Shelah11, Conclusion 10.25])
Let
![]() $\lambda \geq \aleph _1$
. Let
$\lambda \geq \aleph _1$
. Let
![]() ${\mathcal {I}}$
be an ideal on
${\mathcal {I}}$
be an ideal on
![]() $\omega $
and A a set which is almost disjoint from every
$\omega $
and A a set which is almost disjoint from every
![]() $B \in {\mathcal {I}}$
. Then there exists a regular ultrafilter
$B \in {\mathcal {I}}$
. Then there exists a regular ultrafilter
![]() $\mathcal {D}$
on
$\mathcal {D}$
on
![]() $\lambda $
which handles every
$\lambda $
which handles every
![]() $T_{\mathfrak {m}[B]}$
for
$T_{\mathfrak {m}[B]}$
for
![]() $B \in {\mathcal {I}}$
and does not handle
$B \in {\mathcal {I}}$
and does not handle
![]() $T_{\mathfrak {m}[A]}$
. (In the notation of Keisler’s order,
$T_{\mathfrak {m}[A]}$
. (In the notation of Keisler’s order,
![]() $T_{\mathfrak {m}[A]} \not \trianglelefteq T_{\mathfrak {m}[B]}$
for every such
$T_{\mathfrak {m}[A]} \not \trianglelefteq T_{\mathfrak {m}[B]}$
for every such
![]() $T_{\mathfrak {m}[B]}$
.)
$T_{\mathfrak {m}[B]}$
.)
Note that in the language of Theorem B, if
![]() ${\mathcal {I}}$
is countable and T is the theory corresponding to the “disjoint union” of the theories
${\mathcal {I}}$
is countable and T is the theory corresponding to the “disjoint union” of the theories
![]() $T_{\mathfrak {m}[B]}$
for
$T_{\mathfrak {m}[B]}$
for
![]() $B \in {\mathcal {I}}$
, then a regular ultrafilter
$B \in {\mathcal {I}}$
, then a regular ultrafilter
![]() $\mathcal {D}$
handles every
$\mathcal {D}$
handles every
![]() $T_{\mathfrak {m}[B]}$
if and only if it handles T. Theorem B suggests that in order for Keisler’s order to separate theories, their sets of active levels should be quite different in the sense of the ideals they generate. Here is a theorem which says, in a certain case, this is a characterization: condition (1) says, informally, “some ultrafilter picks out precisely these theories from our family to saturate.”
$T_{\mathfrak {m}[B]}$
if and only if it handles T. Theorem B suggests that in order for Keisler’s order to separate theories, their sets of active levels should be quite different in the sense of the ideals they generate. Here is a theorem which says, in a certain case, this is a characterization: condition (1) says, informally, “some ultrafilter picks out precisely these theories from our family to saturate.”
Theorem C (Theorem 11.10 from [Reference Malliaris and Shelah11])
There is a family of parameters
![]() $\{ \mathfrak {m}[A] : A \subseteq \omega \}$
such that each
$\{ \mathfrak {m}[A] : A \subseteq \omega \}$
such that each
![]() $T_{\mathfrak {m}[A]}$
is countable, complete, and simpleFootnote
2
and the following are equivalent for any
$T_{\mathfrak {m}[A]}$
is countable, complete, and simpleFootnote
2
and the following are equivalent for any
![]() $\lambda \geq 2^{\aleph _0}$
and any set
$\lambda \geq 2^{\aleph _0}$
and any set
![]() $\mathbf {X} \subseteq \mathcal {P}(\omega )$
:
$\mathbf {X} \subseteq \mathcal {P}(\omega )$
:
-
(1) There exists a regular ultrafilter
 $\mathcal {D}$
on
$\mathcal {D}$
on
 $\lambda $
such that
$\lambda $
such that
 $\mathbf {X} = \{ A \subseteq \omega : \mathcal {D} $
is
$\mathbf {X} = \{ A \subseteq \omega : \mathcal {D} $
is
 $(\lambda ^+, T_{\mathfrak {m}[A]})$
-good
$(\lambda ^+, T_{\mathfrak {m}[A]})$
-good
 $\}$
.
$\}$
. -
(2)
 $\mathbf {X} \supseteq [\omega ]^{<\aleph _0}$
is an ideal.
$\mathbf {X} \supseteq [\omega ]^{<\aleph _0}$
is an ideal.
So, before connecting the Keisler complexity of (the theory arising from) a set of active levels to the Turing complexity of a set of natural numbers, we should deal with the fact that Turing degrees are rarely ideals. This motivates the opening move of the next section.
3 Second proof
Observation 3.5. There is an injection
![]() $h: \mathcal {P}(\omega ) \rightarrow \mathcal {P}(\omega )$
which is computable and has computable inverse, so that writing
$h: \mathcal {P}(\omega ) \rightarrow \mathcal {P}(\omega )$
which is computable and has computable inverse, so that writing
![]() $\mathcal {H}$
for the range of h we have:
$\mathcal {H}$
for the range of h we have:
-
(1) The elements of
 $\mathcal {H}$
are almost disjoint, i.e., if
$\mathcal {H}$
are almost disjoint, i.e., if
 $A, B \subseteq \omega $
are disjoint then
$A, B \subseteq \omega $
are disjoint then
 $h(A) \cap h(B)$
is finite.
$h(A) \cap h(B)$
is finite. -
(2) For any two disjoint nonempty
 $\mathbf {X}, \mathbf {Y} \subseteq \mathcal {H}$
and for
$\mathbf {X}, \mathbf {Y} \subseteq \mathcal {H}$
and for
 ${\mathcal {I}}, {\mathcal {J}}$
the ideals of subsets of
${\mathcal {I}}, {\mathcal {J}}$
the ideals of subsets of
 $\mathbb {N}$
generated by
$\mathbb {N}$
generated by
 $\mathbf {X}, \mathbf {Y}$
respectively, and for every
$\mathbf {X}, \mathbf {Y}$
respectively, and for every
 $A \in {\mathcal {I}}$
, A is almost disjoint from every element of
$A \in {\mathcal {I}}$
, A is almost disjoint from every element of
 ${\mathcal {J}}$
.
${\mathcal {J}}$
. -
(3) If in (2) we replace disjoint by “
 $\mathbf {X} \setminus \mathbf {Y} \neq \emptyset $
” then there exists
$\mathbf {X} \setminus \mathbf {Y} \neq \emptyset $
” then there exists
 $A \in {\mathcal {I}}$
such that A is almost disjoint from every element of
$A \in {\mathcal {I}}$
such that A is almost disjoint from every element of
 ${\mathcal {J}}$
.
${\mathcal {J}}$
.
Proof Fix a computable bijection between
![]() $\mathbb {N}$
and the internal nodes of a binary tree of countable height. Identify each
$\mathbb {N}$
and the internal nodes of a binary tree of countable height. Identify each
![]() $A \subseteq \omega $
with its characteristic function, which uniquely determines a branch, and let h send A to the set of integers assigned to nodes on that branch.
$A \subseteq \omega $
with its characteristic function, which uniquely determines a branch, and let h send A to the set of integers assigned to nodes on that branch.
For the rest of the paper, fix
![]() $h: \mathcal {P}(\omega ) \rightarrow \mathcal {H}$
as in Observation 3.5. Recall that
$h: \mathcal {P}(\omega ) \rightarrow \mathcal {H}$
as in Observation 3.5. Recall that
![]() $X \leq _1 Y$
means there is a total computable
$X \leq _1 Y$
means there is a total computable
![]() $1:1$
function such that
$1:1$
function such that
![]() $x \in X$
iff
$x \in X$
iff
![]() $f(x) \in Y$
.
$f(x) \in Y$
.
Remark 3.6.
A and
![]() $h(A)$
are clearly Turing-equivalent, even
$h(A)$
are clearly Turing-equivalent, even
![]() $\equiv _1$
. Thus any Turing degree
$\equiv _1$
. Thus any Turing degree
![]() $\mathbf {a} \subseteq \mathcal {P}(\omega )$
naturally corresponds computably to a countably infinite
$\mathbf {a} \subseteq \mathcal {P}(\omega )$
naturally corresponds computably to a countably infinite
![]() $\mathbf {a}_{\mathcal {H}} = \{ h(A) : A \in \mathbf {a} \} \subseteq \mathcal {H}$
.
$\mathbf {a}_{\mathcal {H}} = \{ h(A) : A \in \mathbf {a} \} \subseteq \mathcal {H}$
.
Convention 3.7. For the rest of the paper, we fix an enumeration
![]() $\{ \psi _e : e < \omega \}$
of Turing machines, so that the program
$\{ \psi _e : e < \omega \}$
of Turing machines, so that the program
![]() $\psi _e$
is computable from the index e and vice versa, and as usual let
$\psi _e$
is computable from the index e and vice versa, and as usual let
![]() $\psi ^A_e$
denote
$\psi ^A_e$
denote
![]() $\psi _e$
with A on the input tape.
$\psi _e$
with A on the input tape.
Notation 3.8. Let
![]() $X_{h, e, A} = h ( ~\{ n < \omega : \psi ^A_e(n)$
halts and outputs
$X_{h, e, A} = h ( ~\{ n < \omega : \psi ^A_e(n)$
halts and outputs
![]() $1 \}~)$
, and let
$1 \}~)$
, and let
![]() $H^A = \langle X_{h, e, A} : e < \omega \rangle $
.
$H^A = \langle X_{h, e, A} : e < \omega \rangle $
.
Observation 3.9. Suppose
![]() $A, B \subseteq \omega $
.
$A, B \subseteq \omega $
.
-
(1) The complexity of
 $H^A$
is exactly that of
$H^A$
is exactly that of
 $A^\prime $
, the jump of A.
$A^\prime $
, the jump of A. -
(2) If A is not Turing-reducible to B, then
 $H^A \setminus H^B \neq \emptyset $
.
$H^A \setminus H^B \neq \emptyset $
.
Proof (1) On one hand,
![]() $A^\prime = \{ n : \varphi ^A_n(n) $
halts
$A^\prime = \{ n : \varphi ^A_n(n) $
halts
![]() $\}$
can be read off from
$\}$
can be read off from
![]() $H^A$
, since there is a computable function f which takes an index n to an index
$H^A$
, since there is a computable function f which takes an index n to an index
![]() $f(n)$
such that for any m,
$f(n)$
such that for any m,
![]() $\psi _{f(n)}(m)$
halts and outputs
$\psi _{f(n)}(m)$
halts and outputs
![]() $1$
if and only if
$1$
if and only if
![]() $\psi _n(m)$
halts. On the other, each
$\psi _n(m)$
halts. On the other, each
![]() $X_{h, e, A}$
is c.e. in A so is
$X_{h, e, A}$
is c.e. in A so is
![]() $\leq _1 A^\prime $
by the Jump Theorem [Reference Soare14, 3.4.3].
$\leq _1 A^\prime $
by the Jump Theorem [Reference Soare14, 3.4.3].
(2) There is a set which is c.e. relative to A and not c.e. relative to B. (By the Jump Theorem, X is c.e. in Y if and only if
![]() $X \leq _1 Y^\prime $
, and
$X \leq _1 Y^\prime $
, and
![]() $X \leq _T Y$
if and only if
$X \leq _T Y$
if and only if
![]() $X^\prime \leq _1 Y^\prime $
. Now
$X^\prime \leq _1 Y^\prime $
. Now
![]() $A^\prime $
is c.e. in A, but
$A^\prime $
is c.e. in A, but
![]() $\neg (A \leq _T B)$
thus
$\neg (A \leq _T B)$
thus
![]() $\neg (A^\prime \leq _1 B^\prime )$
.)
$\neg (A^\prime \leq _1 B^\prime )$
.)
Corollary 3.10. If
![]() $A, B \subseteq \omega $
and A is not Turing-reducible to B then in the notation of Observation 3.5, letting
$A, B \subseteq \omega $
and A is not Turing-reducible to B then in the notation of Observation 3.5, letting
![]() $\mathbf {X} = H^A$
and
$\mathbf {X} = H^A$
and
![]() $\mathbf {Y} = H^B$
, and letting
$\mathbf {Y} = H^B$
, and letting
![]() ${\mathcal {I}}, {\mathcal {J}}$
be the ideals of subsets of
${\mathcal {I}}, {\mathcal {J}}$
be the ideals of subsets of
![]() $\mathbb {N}$
generated by
$\mathbb {N}$
generated by
![]() $\mathbf {X}$
,
$\mathbf {X}$
,
![]() $\mathbf {Y}$
respectively, there is
$\mathbf {Y}$
respectively, there is
![]() $X \in {\mathcal {I}}$
which is almost disjoint from every element of
$X \in {\mathcal {I}}$
which is almost disjoint from every element of
![]() ${\mathcal {J}}$
.
${\mathcal {J}}$
.
Theorem 3.11. There is a Turing functional
![]() $\Phi $
taking
$\Phi $
taking
![]() $A^\prime $
to a theory
$A^\prime $
to a theory
![]() $T_A$
which satisfies:
$T_A$
which satisfies:
-
(a) Each
 $T_A$
is a set of axioms for a complete, countable, simple unstable theory.
$T_A$
is a set of axioms for a complete, countable, simple unstable theory. -
(b)
 $\Phi $
is uniform in the jump: the complexity of
$\Phi $
is uniform in the jump: the complexity of
 $T_A$
is exactly
$T_A$
is exactly
 $A^\prime $
.
$A^\prime $
. -
(c) If A, B are Turing-equivalent then
 $T_A$
and
$T_A$
and
 $T_B$
are model-theoretically the same (i.e., up to renaming of symbols) and computable from each other.
$T_B$
are model-theoretically the same (i.e., up to renaming of symbols) and computable from each other. -
(d) Thus
 $\Phi $
is degree-invariant.
$\Phi $
is degree-invariant. -
(e)
 $A \leq _T B$
if and only if
$A \leq _T B$
if and only if
 $T_A \trianglelefteq T_B$
in Keisler’s order.
$T_A \trianglelefteq T_B$
in Keisler’s order.
Discussion 3.12. Theorem 3.11 can be seen as a best possible effective version of Theorem 1.2 on the Turing degrees, in the sense that we are getting degree invariance with no more power beyond what already accrues from the downward closure in Theorem 1.2.
Proof sketch The work of
![]() $\Phi $
is described explicitly in Section 4, but we give the punchline here. Fix in advance the computable signature given in Section 4, which observe is the union of the partial signatures
$\Phi $
is described explicitly in Section 4, but we give the punchline here. Fix in advance the computable signature given in Section 4, which observe is the union of the partial signatures
![]() $\tau ^{\psi _e}$
for
$\tau ^{\psi _e}$
for
![]() $e < \omega $
. When
$e < \omega $
. When
![]() $\Phi $
receives a set
$\Phi $
receives a set
![]() $A \subseteq \omega $
, it divides its computation among
$A \subseteq \omega $
, it divides its computation among
![]() $\{ \psi ^A_e \}_e$
and proceeds to list the axioms as in Section 4, with
$\{ \psi ^A_e \}_e$
and proceeds to list the axioms as in Section 4, with
![]() $X_{h, e, A}$
(Notation 3.8) determining the rules for predicates in the partial signature
$X_{h, e, A}$
(Notation 3.8) determining the rules for predicates in the partial signature
![]() $\tau ^{\psi _e}$
. There is no nontrivial interaction of predicates across the partial signatures. For each
$\tau ^{\psi _e}$
. There is no nontrivial interaction of predicates across the partial signatures. For each
![]() $\psi _e$
, items (0), (1), (3), (4), and (5) from Section 4 are computable and for (2), (6), and (7) it suffices to know
$\psi _e$
, items (0), (1), (3), (4), and (5) from Section 4 are computable and for (2), (6), and (7) it suffices to know
![]() $X_{h, e, A}$
. Also from, e.g., (2), one can read off the characteristic function of
$X_{h, e, A}$
. Also from, e.g., (2), one can read off the characteristic function of
![]() $X_{h, e, A}$
from the axioms restricted to
$X_{h, e, A}$
from the axioms restricted to
![]() $\tau ^{\psi _e}$
.
$\tau ^{\psi _e}$
.
As for the claims of the Theorem:
(a) This is the work of the earlier paper (see [Reference Malliaris and Shelah11, 2.20 and 2.21]).
(b) The uniformity follows from the description in Section 4. The set of axioms
![]() $T_A$
has exactly the complexity of the jump of A, since to determine
$T_A$
has exactly the complexity of the jump of A, since to determine
![]() $T^A$
it is both necessary and sufficient to know the characteristic functions of all sets computed by all the
$T^A$
it is both necessary and sufficient to know the characteristic functions of all sets computed by all the
![]() $\psi ^A$
’s.
$\psi ^A$
’s.
(c) Suppose
![]() $B \leq _T A$
and we are given
$B \leq _T A$
and we are given
![]() $T_A$
. In the notation of Section 4, in order to generate
$T_A$
. In the notation of Section 4, in order to generate
![]() $T_B \upharpoonright \tau ^{\psi _i}$
it is sufficient to know what
$T_B \upharpoonright \tau ^{\psi _i}$
it is sufficient to know what
![]() $\psi _i$
computes with B on its input tape. Fixing a given means of computing B from A we can computably produce an index
$\psi _i$
computes with B on its input tape. Fixing a given means of computing B from A we can computably produce an index
![]() $e = e(i)$
so that
$e = e(i)$
so that
![]() $\psi _e$
simulates
$\psi _e$
simulates
![]() $\psi ^B_i$
, and then we just copy the axioms of
$\psi ^B_i$
, and then we just copy the axioms of
![]() $T_A \upharpoonright \tau ^{\psi _e}$
replacing each predicate superscripted
$T_A \upharpoonright \tau ^{\psi _e}$
replacing each predicate superscripted
![]() ${\psi _e}$
with the corresponding one superscripted
${\psi _e}$
with the corresponding one superscripted
![]() $\psi _i$
.
$\psi _i$
.
(d) Follows from (c).
(e) If A is Turing-reducible to B, then
![]() $T_{A}$
is interpretable in
$T_{A}$
is interpretable in
![]() $T_{B}$
so
$T_{B}$
so
![]() $T_{A} \trianglelefteq T_{B}$
. If A is not Turing-reducible to B, apply Corollary 3.10 with
$T_{A} \trianglelefteq T_{B}$
. If A is not Turing-reducible to B, apply Corollary 3.10 with
![]() $\mathbf {X} = \{ X_{h, e, A} : e < \omega \}$
and
$\mathbf {X} = \{ X_{h, e, A} : e < \omega \}$
and
![]() $\mathbf {Y} = \{ X_{h, e, B} : e < \omega \}$
, followed by Theorem B.
$\mathbf {Y} = \{ X_{h, e, B} : e < \omega \}$
, followed by Theorem B.
Discussion 3.13. We thank Hirschfeldt for pointing out that this proof also gives an embedding of the enumeration degrees [Reference Cai, Ganchev, Lempp, Miller and Soskova1, Definition 1.1] (and thus, the Turing degrees) into Keisler’s order, replacing the
![]() $\psi _e$
’s by enumeration operators.
$\psi _e$
’s by enumeration operators.
4 The operation of
 $\Phi $
$\Phi $
To justify Theorem 3.11 we look more carefully at the theories constructed in [Reference Malliaris and Shelah11, Section 2], clarifying the computable content. (A motivated model theoretic exposition of these theories is in [Reference Malliaris and Shelah11, Section 3].) Here is a high-level summary of what to look for below. The theories have three kinds of ingredients: a fast-growing sequence of natural numbers, an associated sequence of graphs, and at least one and no more than countably many subsets of
![]() $\omega $
. The signature involves unary and binary predicates. We will fix in advance the sequence of natural numbers and the sequence of graphs. We then observe that everything about these two sequences, and about the unary predicates, may be computably axiomatized. The only remaining ingredient is to list the axioms relating to the subsets of
$\omega $
. The signature involves unary and binary predicates. We will fix in advance the sequence of natural numbers and the sequence of graphs. We then observe that everything about these two sequences, and about the unary predicates, may be computably axiomatized. The only remaining ingredient is to list the axioms relating to the subsets of
![]() $\omega $
, which control the binary predicates. Formally, our operator will take in
$\omega $
, which control the binary predicates. Formally, our operator will take in
![]() $A \subseteq \omega $
and produce the remaining axioms based on the countably many subsets
$A \subseteq \omega $
and produce the remaining axioms based on the countably many subsets
![]() $X_{h, e, A}$
. To determine
$X_{h, e, A}$
. To determine
![]() $T_A$
it will be necessary and sufficient to know the characteristic functions of each of these subsets.
$T_A$
it will be necessary and sufficient to know the characteristic functions of each of these subsets.
4.1 Background step and fixing notation
We choose and fix (a) a rapidly growing sequence
![]() $\langle m_n : n < \omega \rangle $
of natural numbers,Footnote
3
and (b) a sequence
$\langle m_n : n < \omega \rangle $
of natural numbers,Footnote
3
and (b) a sequence
![]() $\langle E_n : n < \omega \rangle $
of graphs where
$\langle E_n : n < \omega \rangle $
of graphs where
![]() $E_n$
has
$E_n$
has
![]() $m_n$
vertices which we identify with
$m_n$
vertices which we identify with
![]() $[0, \dots , m_n-1]$
. A technical point: in
$[0, \dots , m_n-1]$
. A technical point: in
![]() $E_n$
, each vertex is connected to itself.
$E_n$
, each vertex is connected to itself.
-
(a) About
 $\bar {m}$
: the required lower bounds on its growth rate are given in [Reference Malliaris and Shelah11, Definition 6.1]. We can easily choose this sequence to be computable, for instance by using the formula in [Reference Malliaris and Shelah11, 6.1], with equality.
$\bar {m}$
: the required lower bounds on its growth rate are given in [Reference Malliaris and Shelah11, Definition 6.1]. We can easily choose this sequence to be computable, for instance by using the formula in [Reference Malliaris and Shelah11, 6.1], with equality. -
(b) About
 $\bar {E}$
: the requirements on
$\bar {E}$
: the requirements on
 $\bar {E}$
are given in [Reference Malliaris and Shelah11, Definition 6.2], expressing that in each
$\bar {E}$
are given in [Reference Malliaris and Shelah11, Definition 6.2], expressing that in each
 $E_n$
any small set of vertices has a common neighbor, and no large set of vertices does. For our purposes here, [Reference Malliaris and Shelah11, Lemma 6.7] (which proves such sequences exist, via finite random graphs) should be understood as an existence result. Knowing that for each n, some graph
$E_n$
any small set of vertices has a common neighbor, and no large set of vertices does. For our purposes here, [Reference Malliaris and Shelah11, Lemma 6.7] (which proves such sequences exist, via finite random graphs) should be understood as an existence result. Knowing that for each n, some graph
 $E_n$
on
$E_n$
on
 $m_n$
vertices exists which satisfies the requirements, we may generate the sequence computably, for instance at stage n lexicographically ordering the graphs on
$m_n$
vertices exists which satisfies the requirements, we may generate the sequence computably, for instance at stage n lexicographically ordering the graphs on
 $m_n$
vertices and checking in order until we find the first one which works.
$m_n$
vertices and checking in order until we find the first one which works.
In sum, the data of
![]() $\bar {m}$
and
$\bar {m}$
and
![]() $\bar {E}$
can be chosen to be computable, even if perhaps not very efficiently.
$\bar {E}$
can be chosen to be computable, even if perhaps not very efficiently.
Notation: For each n, let
![]() $\mathcal {T}_{1,n} = \mathcal {T}_{2,n}$
be the set of sequences
$\mathcal {T}_{1,n} = \mathcal {T}_{2,n}$
be the set of sequences
![]() $\eta $
of length n such that
$\eta $
of length n such that
![]() $\eta (i) < m_i$
for
$\eta (i) < m_i$
for
![]() $i \leq n$
. (There are two such: a “left tree” and a “right tree,” distinct but symmetric.) Let
$i \leq n$
. (There are two such: a “left tree” and a “right tree,” distinct but symmetric.) Let
![]() $\mathcal {T}_{1,\leq n}$
, or
$\mathcal {T}_{1,\leq n}$
, or
![]() $\mathcal {T}_{2,\leq n}$
mean all such sequences of length
$\mathcal {T}_{2,\leq n}$
mean all such sequences of length
![]() $\leq n$
. (So these are the nodes of a finite tree of height n with
$\leq n$
. (So these are the nodes of a finite tree of height n with
![]() $m_i$
-branching at level i.) Let
$m_i$
-branching at level i.) Let
![]() $\mathcal {T}_{1} = \bigcup _n \mathcal {T}_{1,\leq n} = \mathcal {T}_2 = \bigcup _n \mathcal {T}_{2,\leq n}$
be the sets of all such finite sequences.
$\mathcal {T}_{1} = \bigcup _n \mathcal {T}_{1,\leq n} = \mathcal {T}_2 = \bigcup _n \mathcal {T}_{2,\leq n}$
be the sets of all such finite sequences.
We now describe a set of axioms for a complete, countable theory
![]() $T_A$
, for any
$T_A$
, for any
![]() $A \subseteq \omega $
. The computable signature is
$A \subseteq \omega $
. The computable signature is
where each
![]() $R^\psi $
is a binary predicate and the rest are unary. As a reminder,
$R^\psi $
is a binary predicate and the rest are unary. As a reminder,
![]() $X_{h,e, A}$
denotes the image under h of the set computed by
$X_{h,e, A}$
denotes the image under h of the set computed by
![]() $\psi $
with A on the input tape.
$\psi $
with A on the input tape.
The axioms we will need to enumerate are the following. Observe in these conditions that writing
![]() $\tau ^\psi $
for the restriction of
$\tau ^\psi $
for the restriction of
![]() $\tau $
to predicates superscripted by a specific Turing machine
$\tau $
to predicates superscripted by a specific Turing machine
![]() $\psi $
, the only nontrivial interactions between predicates are among those in the same
$\psi $
, the only nontrivial interactions between predicates are among those in the same
![]() $\tau ^\psi $
, and indeed one can think of the resulting theory as the disjoint union of its restriction to each
$\tau ^\psi $
, and indeed one can think of the resulting theory as the disjoint union of its restriction to each
![]() $\tau ^\psi $
.
$\tau ^\psi $
.
-
(0) For each
 $\psi _i, \psi _j$
a universal axiom stating that
$\psi _i, \psi _j$
a universal axiom stating that
 $(\mathcal {Q}^{\psi _i} \cup \mathcal {P}^{\psi _i}) \cap (\mathcal {Q}^{\psi _j} \cup \mathcal {P}^{\psi _j}) = \emptyset $
whenever
$(\mathcal {Q}^{\psi _i} \cup \mathcal {P}^{\psi _i}) \cap (\mathcal {Q}^{\psi _j} \cup \mathcal {P}^{\psi _j}) = \emptyset $
whenever
 $i \neq j$
.
$i \neq j$
.
-
(1) For every
 $n<\omega $
and each
$n<\omega $
and each
 $\psi $
, universal axioms stating that:Footnote
4
$\psi $
, universal axioms stating that:Footnote
4
-
•
 $\mathcal {Q}^\psi $
and
$\mathcal {Q}^\psi $
and
 $\mathcal {P}^\psi $
are disjoint. Identify
$\mathcal {P}^\psi $
are disjoint. Identify
 $\mathcal {Q}^\psi $
and
$\mathcal {Q}^\psi $
and
 $Q^\psi _{\langle \rangle }$
,
$Q^\psi _{\langle \rangle }$
,
 $\mathcal {P}^\psi $
and
$\mathcal {P}^\psi $
and
 $P^\psi _{\langle \rangle }$
.
$P^\psi _{\langle \rangle }$
. -
•
 $\langle Q^\psi _{\eta } : \eta \in \mathcal {T}_{1, m} \rangle $
partitions
$\langle Q^\psi _{\eta } : \eta \in \mathcal {T}_{1, m} \rangle $
partitions
 $\mathcal {Q}^\psi $
for each
$\mathcal {Q}^\psi $
for each
 $m\leq n$
and this partition satisfies
$m\leq n$
and this partition satisfies
 $ \eta ^\prime \trianglelefteq \eta \in \mathcal {T}_{1, \leq k} \mbox { implies } Q^\psi _{\eta ^\prime } \supseteq Q^\psi _\eta $
. (Concentric predicates represent advancing along a branch.)
$ \eta ^\prime \trianglelefteq \eta \in \mathcal {T}_{1, \leq k} \mbox { implies } Q^\psi _{\eta ^\prime } \supseteq Q^\psi _\eta $
. (Concentric predicates represent advancing along a branch.) -
•
 $\langle P^\psi _{\nu } : \nu \in \mathcal {T}_{2, m} \rangle $
partitions
$\langle P^\psi _{\nu } : \nu \in \mathcal {T}_{2, m} \rangle $
partitions
 $\mathcal {P}^\psi $
for each
$\mathcal {P}^\psi $
for each
 $m\leq n$
and this partition satisfies
$m\leq n$
and this partition satisfies
 $ \nu ^\prime \trianglelefteq \nu \in \mathcal {T}_{2,\leq k} \mbox { implies }P^\psi _{\nu ^\prime } \supseteq P^\psi _\nu $
. (The same on the other side.)
$ \nu ^\prime \trianglelefteq \nu \in \mathcal {T}_{2,\leq k} \mbox { implies }P^\psi _{\nu ^\prime } \supseteq P^\psi _\nu $
. (The same on the other side.) -
•
 $R^\psi \subseteq \mathcal {Q}^\psi \times \mathcal {P}^\psi $
. (
$R^\psi \subseteq \mathcal {Q}^\psi \times \mathcal {P}^\psi $
. (
 $\mathcal {R}^\psi $
holds between elements of
$\mathcal {R}^\psi $
holds between elements of
 $\mathcal {Q}^\psi $
and of
$\mathcal {Q}^\psi $
and of
 $\mathcal {P}^\psi $
.)
$\mathcal {P}^\psi $
.)
-
-
(2) If
 $n \in X_{h, e, A}$
, add a universal axiom saying “n is an active level,” meaning:
$n \in X_{h, e, A}$
, add a universal axiom saying “n is an active level,” meaning:-
•
 $R^{\psi _e}(x,y)$
only if for some
$R^{\psi _e}(x,y)$
only if for some
 $\eta _1 \in \mathcal {T}_{1, n}$
and
$\eta _1 \in \mathcal {T}_{1, n}$
and
 $\eta _2 \in \mathcal {T}_{2, n}$
, we have
$\eta _2 \in \mathcal {T}_{2, n}$
, we have
 $Q^{\psi _e}_{\eta _1}(x)$
and
$Q^{\psi _e}_{\eta _1}(x)$
and
 $P^{\psi _e}_{\eta _2}(y)$
and in the graph
$P^{\psi _e}_{\eta _2}(y)$
and in the graph
 $E_{n}$
there is an edge between
$E_{n}$
there is an edge between
 $\eta _1(n-1)$
and
$\eta _1(n-1)$
and
 $\eta _2(n-1)$
.Footnote
5
$\eta _2(n-1)$
.Footnote
5
Informally, at “active levels” we put new constraints on the behavior of
 $R^{\psi _e}$
, and at non-active (“lazy”) levels there are no new constraints.
$R^{\psi _e}$
, and at non-active (“lazy”) levels there are no new constraints.The axioms so far enumerate a universal theory; we would like to axiomatize its model completion. Corollary 2.20 and Conclusion 2.21 of [Reference Malliaris and Shelah11] show this model completion exists and is quite simple, for instance it eliminates quantifiers. The remaining axioms give the necessary information.
-
-
(3) For each k, and each
 $\eta \in \mathcal {T}_{1,\leq k}$
an axiom saying: whether there exists x in
$\eta \in \mathcal {T}_{1,\leq k}$
an axiom saying: whether there exists x in
 $Q^{\psi _e}_\eta $
which is
$Q^{\psi _e}_\eta $
which is
 $R^{\psi _e}$
-connected to
$R^{\psi _e}$
-connected to
 $y_1, \dots , y_k$
and not to
$y_1, \dots , y_k$
and not to
 $z_1, \dots , z_k$
, all in
$z_1, \dots , z_k$
, all in
 $\mathcal {P}^{\psi _e}$
, depends on the quantifier-free type of
$\mathcal {P}^{\psi _e}$
, depends on the quantifier-free type of
 $y_1, \dots , y_k, z_1, \dots , z_k$
restricted to the finite signature
$y_1, \dots , y_k, z_1, \dots , z_k$
restricted to the finite signature
 $\{ Q^{\psi _e}_{\eta } : \eta \in \mathcal {T}_{1, \leq k} \} \cup \{ P^{\psi _e}_\eta : \eta \in \mathcal {T}_{2, \leq k} \}$
. (This can be expressed in terms of complete formulas in the variables
$\{ Q^{\psi _e}_{\eta } : \eta \in \mathcal {T}_{1, \leq k} \} \cup \{ P^{\psi _e}_\eta : \eta \in \mathcal {T}_{2, \leq k} \}$
. (This can be expressed in terms of complete formulas in the variables
 $y_i$
,
$y_i$
,
 $z_j$
which specify the unary predicates for each variable, along with equalities and inequalities.)
$z_j$
which specify the unary predicates for each variable, along with equalities and inequalities.) -
(4) Parallel to (3), swapping Q/P,
 $T_{1,k}$
/
$T_{1,k}$
/
 $T_{2,k}$
, and changing the direction of R.
$T_{2,k}$
, and changing the direction of R. -
(5) For each k, an axiom saying: there exists x in
 $\mathcal {Q}^{\psi _e}$
which is
$\mathcal {Q}^{\psi _e}$
which is
 $R^{\psi _e}$
-connected to
$R^{\psi _e}$
-connected to
 $y_1, \dots , y_k$
and not to
$y_1, \dots , y_k$
and not to
 $z_1, \dots , z_k$
, all in
$z_1, \dots , z_k$
, all in
 $\mathcal {P}^{\psi _e}$
, if and only if (
$\mathcal {P}^{\psi _e}$
, if and only if (
 $\{ y_1, \dots , y_k \} \cap \{ z_1, \dots , z_k \} = \emptyset $
and there exists
$\{ y_1, \dots , y_k \} \cap \{ z_1, \dots , z_k \} = \emptyset $
and there exists
 $x R^{\psi _e}$
-connected to
$x R^{\psi _e}$
-connected to
 $y_1, \dots , y_k$
). (If the formula is not inconsistent, it reduces to the positive part. Since
$y_1, \dots , y_k$
). (If the formula is not inconsistent, it reduces to the positive part. Since
 $R^{\psi _e}$
is not symmetric, we have two copies of any such axiom, swapping
$R^{\psi _e}$
is not symmetric, we have two copies of any such axiom, swapping
 $\mathcal {P}^{\psi _e}(x)$
for
$\mathcal {P}^{\psi _e}(x)$
for
 $\mathcal {Q}^{\psi _e}(x)$
.)
$\mathcal {Q}^{\psi _e}(x)$
.) -
(6) For each choice of
-
• k,
-
•
 $\rho \in \mathcal {T}_{1,k}$
and
$\rho \in \mathcal {T}_{1,k}$
and
 $\nu _1, \dots , \nu _k \in \mathcal {T}_{2,k}$
, such that for all
$\nu _1, \dots , \nu _k \in \mathcal {T}_{2,k}$
, such that for all
 $t \leq k$
,if
$t \leq k$
,if
 $t \in X_{h, e, A}$
then
$t \in X_{h, e, A}$
then
 $(\rho (t-1), \nu _i(t-1)) \in E_{t}$
,
$(\rho (t-1), \nu _i(t-1)) \in E_{t}$
, -
• complete quantifier-free formula
 $\theta (y_1,\dots , y_k)$
in the free variables
$\theta (y_1,\dots , y_k)$
in the free variables
 $y_1,\dots , y_k$
such that
$y_1,\dots , y_k$
such that
 $\theta (y_1,\dots , y_k)$
implies
$\theta (y_1,\dots , y_k)$
implies
 $P^{\psi _e}_{\nu _1}(y_1) \land \cdots \land P^{\psi _e}_{\nu _k}(y_k)$
,
$P^{\psi _e}_{\nu _1}(y_1) \land \cdots \land P^{\psi _e}_{\nu _k}(y_k)$
,
an axiom saying:
(The fact that these are the only cases where such x’s will exist follows from the list in (2), and notice that it’s enough to say this works for some such $$\begin{align*}(\exists y_1, \dots, y_n)(\exists x)\left(\theta(y_1, \dots, y_n) \land Q^{\psi_e}_\rho(x) \land \bigwedge_{1 \leq i \leq k} R^{\psi_e}(x,y_i)\right). \end{align*}$$
$$\begin{align*}(\exists y_1, \dots, y_n)(\exists x)\left(\theta(y_1, \dots, y_n) \land Q^{\psi_e}_\rho(x) \land \bigwedge_{1 \leq i \leq k} R^{\psi_e}(x,y_i)\right). \end{align*}$$
 $y_1,\dots , y_n$
because of (3).)
$y_1,\dots , y_n$
because of (3).)
-
-
(7) Parallel to (6), swapping
 $Q^{\psi _e}$
’s and
$Q^{\psi _e}$
’s and
 $P^{\psi _e}$
’s,
$P^{\psi _e}$
’s,
 $\mathcal {T}_{1}$
and
$\mathcal {T}_{1}$
and
 $\mathcal {T}_{2}$
, and changing the direction of
$\mathcal {T}_{2}$
, and changing the direction of
 $R^{\psi _e}$
.
$R^{\psi _e}$
.
From the above axioms, it should be clear that for each
![]() $A \subseteq \omega $
and for each
$A \subseteq \omega $
and for each
![]() ${\psi _e}$
, the theory
${\psi _e}$
, the theory
![]() $T_A$
restricted to the signature
$T_A$
restricted to the signature
![]() $\tau ^{\psi _e}$
is determined by the subset
$\tau ^{\psi _e}$
is determined by the subset
![]() $X_{h, e, A}$
, and in turn determines it.
$X_{h, e, A}$
, and in turn determines it.
Remark 4.14. As it is now clear how the theories depend on subsets of
![]() $\omega $
, we note that the “
$\omega $
, we note that the “
![]() $\mathfrak {m}$
” notation of Section 2 records this also. That is, each theory
$\mathfrak {m}$
” notation of Section 2 records this also. That is, each theory
![]() $T_A \upharpoonright \tau ^{\psi _e}$
here is model-theoretically the same as
$T_A \upharpoonright \tau ^{\psi _e}$
here is model-theoretically the same as
![]() $T_{\mathfrak {m}[X_{h,e,A}]}$
there, under the interpretation corresponding to erasing the superscript
$T_{\mathfrak {m}[X_{h,e,A}]}$
there, under the interpretation corresponding to erasing the superscript
![]() ${\psi _e}$
from each of the predicates. Moreover, in model theoretic language, our theory
${\psi _e}$
from each of the predicates. Moreover, in model theoretic language, our theory
![]() $T_A$
and the theory which is the disjoint union of the theories
$T_A$
and the theory which is the disjoint union of the theories
![]() $\{ T_{\mathfrak {m}[X_{h, e, A}]} : e < \omega \} $
can each be interpreted in the other.
$\{ T_{\mathfrak {m}[X_{h, e, A}]} : e < \omega \} $
can each be interpreted in the other.
5 On avoiding the jump
As noted above, Theorem 3.11 is very natural because of its relation to Theorem 1.2. However, we thank the referee for encouraging us to consider whether some other operator may be found which is uniform in A rather than
![]() $A^\prime $
. A priori, this may seem unlikely, and indeed, a priori, the above theories do not seem adapted to answer this question; they can even be seen as orthogonal to it, since they were built to interact with each other in some sense as freely as possible. Already in [Reference Malliaris and Shelah11] some kind of disjoint union was needed whenever a dependence was called for. This is related to the fact that Keisler’s order quantifies over all regular ultrafilters.
$A^\prime $
. A priori, this may seem unlikely, and indeed, a priori, the above theories do not seem adapted to answer this question; they can even be seen as orthogonal to it, since they were built to interact with each other in some sense as freely as possible. Already in [Reference Malliaris and Shelah11] some kind of disjoint union was needed whenever a dependence was called for. This is related to the fact that Keisler’s order quantifies over all regular ultrafilters.
In this concluding section we prove, perhaps quite surprisingly, that the answer is yes. The construction will build on what was done above, essentially by modifying the previous section in ways which are important for computability and unimportant for model theory. It is best to read with an understanding of the proof of Theorem 3.11.
We fix as before an enumeration
![]() $\{ \psi _e : e < \omega \}$
of Turing machines, and working towards Theorem 5.16, we shall now describe the operation of
$\{ \psi _e : e < \omega \}$
of Turing machines, and working towards Theorem 5.16, we shall now describe the operation of
![]() $\Psi $
which takes in
$\Psi $
which takes in
![]() $A \subseteq \omega $
and outputs a set of axioms
$A \subseteq \omega $
and outputs a set of axioms
![]() $T^*_A$
. Similarly to the earlier case,
$T^*_A$
. Similarly to the earlier case,
![]() $T^*_A$
will be the disjoint union of axioms
$T^*_A$
will be the disjoint union of axioms
![]() $T^*_{e, A}$
for
$T^*_{e, A}$
for
![]() $e < \omega $
. We shall fix A and e and describe
$e < \omega $
. We shall fix A and e and describe
![]() $T^*_{e, A}$
.
$T^*_{e, A}$
.
Let
![]() $X_{h, e, A}$
be as in Notation 3.8 and let
$X_{h, e, A}$
be as in Notation 3.8 and let
![]() $\chi _{h, e, A}$
denote the partial characteristic function of the h-image of the set computed by
$\chi _{h, e, A}$
denote the partial characteristic function of the h-image of the set computed by
![]() $\psi ^A_e$
, that is, for
$\psi ^A_e$
, that is, for
![]() $\mathbf {t} \in \{ 0, 1 \}$
,
$\mathbf {t} \in \{ 0, 1 \}$
,
![]() $\chi _{h, e, A}(n) = \mathbf {t}$
if and only if
$\chi _{h, e, A}(n) = \mathbf {t}$
if and only if
![]() $\psi ^A_e$
halts on input
$\psi ^A_e$
halts on input
![]() $h^{-1}(n)$
and outputs
$h^{-1}(n)$
and outputs
![]() $\mathbf {t}$
. Let
$\mathbf {t}$
. Let
![]() $\chi _{h, e, A}(n, k) = \mathbf {t}$
mean that
$\chi _{h, e, A}(n, k) = \mathbf {t}$
mean that
![]() $\psi ^A_e$
halts after exactly k steps on input
$\psi ^A_e$
halts after exactly k steps on input
![]() $h^{-1}(n)$
and outputs
$h^{-1}(n)$
and outputs
![]() $\mathbf {t}$
.
$\mathbf {t}$
.
The computable signature for
![]() $T^*_{e,A}$
will be (note here e is fixed):
$T^*_{e,A}$
will be (note here e is fixed):
where
![]() $R^{\psi _e}$
is a binary predicate and the rest are unary.
$R^{\psi _e}$
is a binary predicate and the rest are unary.
Discussion 5.15 (Informal explanation/intention)
We start at level
![]() $0$
with countably many copies of the predicate
$0$
with countably many copies of the predicate
![]() $Q_{\langle \rangle }$
, indexed as
$Q_{\langle \rangle }$
, indexed as
![]() $Q_{\langle \rangle , \langle k \rangle }$
for
$Q_{\langle \rangle , \langle k \rangle }$
for
![]() $k <\omega $
. We start running
$k <\omega $
. We start running
![]() $\psi ^A_e$
on input
$\psi ^A_e$
on input
![]() $h^{-1}(0)$
, where observe
$h^{-1}(0)$
, where observe
![]() $0 = \operatorname {lg} (\langle \rangle )$
. If after exactly k steps the computation halts, specify that
$0 = \operatorname {lg} (\langle \rangle )$
. If after exactly k steps the computation halts, specify that
![]() $Q_{\langle \rangle , \langle k \rangle }$
is nonempty, else specify it is empty. Do the same on the other side for the
$Q_{\langle \rangle , \langle k \rangle }$
is nonempty, else specify it is empty. Do the same on the other side for the
![]() $P_{\langle \rangle , \langle k \rangle }$
’s. In this case
$P_{\langle \rangle , \langle k \rangle }$
’s. In this case
![]() $\rho $
is a sequence of integers of length one. So for all but at most one
$\rho $
is a sequence of integers of length one. So for all but at most one
![]() $\rho $
on each side (and if one exists, it is the same
$\rho $
on each side (and if one exists, it is the same
![]() $\rho $
), these predicates will be empty, and all these decisions are clearly computable. If this computation does halt after exactly
$\rho $
), these predicates will be empty, and all these decisions are clearly computable. If this computation does halt after exactly
![]() $k_0$
steps, then: if the output is
$k_0$
steps, then: if the output is
![]() $1$
, add axioms saying that
$1$
, add axioms saying that
![]() $0$
is an active level (i.e., for
$0$
is an active level (i.e., for
![]() $Q_{\langle \rangle , \langle k_0 \rangle }$
and
$Q_{\langle \rangle , \langle k_0 \rangle }$
and
![]() $P_{\langle \rangle , \langle k_0 \rangle }$
), if not, just add an axiom saying
$P_{\langle \rangle , \langle k_0 \rangle }$
), if not, just add an axiom saying
![]() $\mathcal {R} \subseteq Q_{\langle \rangle , \langle k_0 \rangle } \times P_{\langle \rangle , \langle k_0 \rangle }$
. Now we deal with level
$\mathcal {R} \subseteq Q_{\langle \rangle , \langle k_0 \rangle } \times P_{\langle \rangle , \langle k_0 \rangle }$
. Now we deal with level
![]() $1$
. For each predicate of the form
$1$
. For each predicate of the form
![]() $Q_{\langle a \rangle , \rho }$
where
$Q_{\langle a \rangle , \rho }$
where
![]() $\rho = \langle i_0, i_1 \rangle $
, we have an axiom saying that
$\rho = \langle i_0, i_1 \rangle $
, we have an axiom saying that
![]() $Q_{\langle a \rangle , \langle i_0, i_1 \rangle } \subseteq Q_{\langle \rangle , \langle i_0 \rangle }$
so most of these are immediately empty, unless
$Q_{\langle a \rangle , \langle i_0, i_1 \rangle } \subseteq Q_{\langle \rangle , \langle i_0 \rangle }$
so most of these are immediately empty, unless
![]() $k_0$
from level 0 exists and
$k_0$
from level 0 exists and
![]() $i_0 = k_0$
. In this case, we run
$i_0 = k_0$
. In this case, we run
![]() $\psi ^A_e$
on input
$\psi ^A_e$
on input
![]() $h^{-1}(1)$
and if after exactly k steps the computation halts, specify that
$h^{-1}(1)$
and if after exactly k steps the computation halts, specify that
![]() $Q_{\langle a \rangle , \langle k_0, k \rangle } \neq \emptyset $
, else specify it is empty. Do the same on the other side for the
$Q_{\langle a \rangle , \langle k_0, k \rangle } \neq \emptyset $
, else specify it is empty. Do the same on the other side for the
![]() $P_{\langle a \rangle , \langle k_0, k \rangle }$
’s. If the computation does halt after exactly
$P_{\langle a \rangle , \langle k_0, k \rangle }$
’s. If the computation does halt after exactly
![]() $k_1$
steps, then if the output is
$k_1$
steps, then if the output is
![]() $1$
, add axioms saying that
$1$
, add axioms saying that
![]() $1$
is an active level, if not, just specify that
$1$
is an active level, if not, just specify that
![]() $\mathcal {R} \subseteq \bigcup _a Q_{\langle a \rangle , \langle k_0, k_1 \rangle } \times \bigcup _b P_{\langle b \rangle , \langle k_0, k_1 \rangle }$
. And so forth. In some sense, we are choosing an “isomorphic copy” of the theory from the previous section which exists as a choice of a computable branch in a tree of computations.
$\mathcal {R} \subseteq \bigcup _a Q_{\langle a \rangle , \langle k_0, k_1 \rangle } \times \bigcup _b P_{\langle b \rangle , \langle k_0, k_1 \rangle }$
. And so forth. In some sense, we are choosing an “isomorphic copy” of the theory from the previous section which exists as a choice of a computable branch in a tree of computations.
The axioms are as follows. We will temporarily drop the superscript
![]() $\psi _e$
, and writing “
$\psi _e$
, and writing “
![]() $Q_{\eta , \rho }$
” assumes the two subscripts have appropriate and compatible lengths.
$Q_{\eta , \rho }$
” assumes the two subscripts have appropriate and compatible lengths.
-
(1)
 $Q_{\langle \rangle , \rho } \cap P_{\langle \rangle , \rho } = \emptyset $
.
$Q_{\langle \rangle , \rho } \cap P_{\langle \rangle , \rho } = \emptyset $
. -
(2)
 $Q_{\eta _1, \rho _1} \supseteq Q_{\eta _2, \rho _2}$
if
$Q_{\eta _1, \rho _1} \supseteq Q_{\eta _2, \rho _2}$
if
 $\eta _1 \trianglelefteq \eta _2$
,
$\eta _1 \trianglelefteq \eta _2$
,
 $\rho _1 \trianglelefteq \rho _2$
, and likewise for P.
$\rho _1 \trianglelefteq \rho _2$
, and likewise for P. -
(3) The predicates
 $Q_{\eta ^\smallfrown \langle \ell \rangle , \rho }$
partition
$Q_{\eta ^\smallfrown \langle \ell \rangle , \rho }$
partition
 $Q_{\eta , \rho \upharpoonright _{\operatorname {lg}(\eta ) + 1}}$
, and likewise for P.
$Q_{\eta , \rho \upharpoonright _{\operatorname {lg}(\eta ) + 1}}$
, and likewise for P. -
(4) Consider
 $Q_{\eta , \rho }$
where
$Q_{\eta , \rho }$
where
 $\operatorname {lg}(\eta ) = n$
. If
$\operatorname {lg}(\eta ) = n$
. If
 $\psi ^A_e$
on input
$\psi ^A_e$
on input
 $h^{-1}(n)$
halts after exactly
$h^{-1}(n)$
halts after exactly
 $\rho (n)$
steps, after having completed the previous computation, then add an axiom saying
$\rho (n)$
steps, after having completed the previous computation, then add an axiom saying
 $Q_{\eta , \rho }$
is nonempty, otherwise add an axiom saying
$Q_{\eta , \rho }$
is nonempty, otherwise add an axiom saying
 $Q_{\eta , \rho }$
is empty. Furthermore, if
$Q_{\eta , \rho }$
is empty. Furthermore, if
 $\psi ^A_e$
on input
$\psi ^A_e$
on input
 $h^{-1}(n)$
halts after exactly
$h^{-1}(n)$
halts after exactly
 $\rho (n)$
steps and outputs 1, add an axiom saying “n is an active level,” i.e.,
$\rho (n)$
steps and outputs 1, add an axiom saying “n is an active level,” i.e.,
 $R(x,y)$
if and only if for some
$R(x,y)$
if and only if for some
 $\eta _1 \in \mathcal {T}_{1,n}$
and
$\eta _1 \in \mathcal {T}_{1,n}$
and
 $\eta _2 \in \mathcal {T}_{2,n}$
we have
$\eta _2 \in \mathcal {T}_{2,n}$
we have
 $Q_{\eta _1, \rho }(x)$
and
$Q_{\eta _1, \rho }(x)$
and
 $P_{\eta _2, \rho }(y)$
and in
$P_{\eta _2, \rho }(y)$
and in
 $E_n$
there is an edge between
$E_n$
there is an edge between
 $\eta _1(n-1)$
and
$\eta _1(n-1)$
and
 $\eta _2(n-1)$
.
$\eta _2(n-1)$
. -
(5) Add the analogues of the computable axioms (3)–(5) above, quantifying over
 $\rho $
of the appropriate length.
$\rho $
of the appropriate length. -
(6) For each choice of
-
• m,
-
•
 $\eta \in \mathcal {T}_{1,m}$
and
$\eta \in \mathcal {T}_{1,m}$
and
 $\nu _1, \dots , \nu _m \in \mathcal {T}_{2,m}$
, such that for all
$\nu _1, \dots , \nu _m \in \mathcal {T}_{2,m}$
, such that for all
 $\ell \leq m$
,
$\ell \leq m$
,
 $\psi ^A_e$
on input
$\psi ^A_e$
on input
 $h^{-1}(\ell )$
halts after exactly
$h^{-1}(\ell )$
halts after exactly
 $\rho (\ell )$
steps, and if it halts and outputs
$\rho (\ell )$
steps, and if it halts and outputs
 $1$
then
$1$
then
 $(\eta (\ell -1), \nu _i(\ell -1)) \in E_\ell $
for
$(\eta (\ell -1), \nu _i(\ell -1)) \in E_\ell $
for
 $1 \leq i \leq m$
,
$1 \leq i \leq m$
, -
• complete quantifier-free formula
 $\theta (y_1,\dots , y_m)$
in the free variables
$\theta (y_1,\dots , y_m)$
in the free variables
 $y_1,\dots , y_m$
such that
$y_1,\dots , y_m$
such that
 $\theta (y_1,\dots , y_m)$
implies
$\theta (y_1,\dots , y_m)$
implies
 $P_{\nu _1, \rho }(y_1) \land \cdots \land P_{\nu _m, \rho }(y_m)$
,
$P_{\nu _1, \rho }(y_1) \land \cdots \land P_{\nu _m, \rho }(y_m)$
,
an axiom saying:
 $$\begin{align*}(\exists y_1, \dots, y_n)(\exists x)\left(\theta(y_1, \dots, y_n) \land Q_{\eta, \rho}(x) \land \bigwedge_{1 \leq i \leq m} R(x,y_i)\right). \end{align*}$$
$$\begin{align*}(\exists y_1, \dots, y_n)(\exists x)\left(\theta(y_1, \dots, y_n) \land Q_{\eta, \rho}(x) \land \bigwedge_{1 \leq i \leq m} R(x,y_i)\right). \end{align*}$$
-
-
(7) Parallel to (6), swapping Q’s and P’s,
 $\mathcal {T}_{1}$
and
$\mathcal {T}_{1}$
and
 $\mathcal {T}_{2}$
, and changing the direction of R.
$\mathcal {T}_{2}$
, and changing the direction of R.
Observe the following:
(a) The axioms are computable in A.
(b) There is at most one
![]() $\rho _* \in {^{\omega } \omega }$
such that for all n, for some (in fact, all)
$\rho _* \in {^{\omega } \omega }$
such that for all n, for some (in fact, all)
![]() $\eta \in \mathcal {T}_{1,n}$
and
$\eta \in \mathcal {T}_{1,n}$
and
![]() $\nu \in \mathcal {T}_{2,n}$
, we have that
$\nu \in \mathcal {T}_{2,n}$
, we have that
![]() $Q_{\eta , \rho _* \upharpoonright _{n+1}}$
is nonempty and
$Q_{\eta , \rho _* \upharpoonright _{n+1}}$
is nonempty and
![]() $P_{\nu , \rho _* \upharpoonright _{n+1}}$
is nonempty.
$P_{\nu , \rho _* \upharpoonright _{n+1}}$
is nonempty.
(c) If
![]() $\psi ^A_e$
is not a total function then all but finitely many of the predicates are empty, and thus by the earlier paper [Reference Malliaris and Shelah11],
$\psi ^A_e$
is not a total function then all but finitely many of the predicates are empty, and thus by the earlier paper [Reference Malliaris and Shelah11],
![]() $T^*_A$
is Keisler-equivalent to the random graph, which is the minimum simple unstable theory in Keisler’s order.
$T^*_A$
is Keisler-equivalent to the random graph, which is the minimum simple unstable theory in Keisler’s order.
(d) Not only is
![]() $T^*_A$
computable from A, but also we can read off A from
$T^*_A$
computable from A, but also we can read off A from
![]() $T^*_A$
(for instance, if we choose in advance one of the
$T^*_A$
(for instance, if we choose in advance one of the
![]() $\psi $
’s which we know computes the identity). So its complexity is exactly that of A.
$\psi $
’s which we know computes the identity). So its complexity is exactly that of A.
(e) Using the notation of the previous section,
![]() $T^*_A$
is model-theoretically equivalent to the disjoint union of theories whose active levels are those
$T^*_A$
is model-theoretically equivalent to the disjoint union of theories whose active levels are those
![]() $X_{h,e,A}$
for which
$X_{h,e,A}$
for which
![]() $\psi ^A_e$
is a total function. Thus, the analysis of the previous section goes through and
$\psi ^A_e$
is a total function. Thus, the analysis of the previous section goes through and
![]() $T^*_A \trianglelefteq T^*_B$
in Keisler’s order if and only if
$T^*_A \trianglelefteq T^*_B$
in Keisler’s order if and only if
![]() $A \leq _T B$
. However,
$A \leq _T B$
. However,
![]() $T^*_A$
is not computability-theoretically more complicated than A, because we have distributed the information of the jump across infinitely many copies of the predicates.
$T^*_A$
is not computability-theoretically more complicated than A, because we have distributed the information of the jump across infinitely many copies of the predicates.
So we may conclude:
Theorem 5.16. There is a Turing machine
![]() $\Psi $
sending sets
$\Psi $
sending sets
![]() $A \subseteq \omega $
to theories
$A \subseteq \omega $
to theories
![]() $T^*_A$
which satisfies:
$T^*_A$
which satisfies:
-
(a) Each
 $T^*_A$
is a set of axioms for a complete, countable, simple unstable theory.
$T^*_A$
is a set of axioms for a complete, countable, simple unstable theory. -
(b)
 $\Psi $
is uniform in A: the complexity of
$\Psi $
is uniform in A: the complexity of
 $T^*_A$
is exactly that of A.
$T^*_A$
is exactly that of A. -
(c) If A, B are Turing-equivalent then
 $T^*_A$
and
$T^*_A$
and
 $T^*_B$
are model-theoretically the same (i.e., up to renaming of symbols).
$T^*_B$
are model-theoretically the same (i.e., up to renaming of symbols). -
(d) Thus
 $\Psi $
is degree-invariant.
$\Psi $
is degree-invariant. -
(e)
 $A \leq _T B$
if and only if
$A \leq _T B$
if and only if
 $T^*_A \trianglelefteq T^*_B$
in Keisler’s order.
$T^*_A \trianglelefteq T^*_B$
in Keisler’s order.
Acknowledgments
Research partially supported by NSF-BSF (NSF 2051825 and BSF 3013005232). This is paper 1222 in Shelah’s list.