Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T22:06:40.907Z Has data issue: false hasContentIssue false
  • English
  • Français

RAMSEY-LIKE THEOREMS AND MODULI OF COMPUTATION

Part of: Computability and recursion theory General logic

Published online by Cambridge University Press:  27 October 2020

LUDOVIC PATEY
LUDOVIC PATEY*
Affiliation:
CN RS, INSTITUT CAMILLE JORDAN UNIVERSITÉ CLAUDE BERNARD LYON 1 43 BOULEVARD DU 11 NOVEMBRE 1918 F-69622 VILLEURBANNE CEDEX, FRANCEE-mail: ludovic.patey@computability.frURL: http://ludovicpatey.com
Get access Rights & Permissions [Opens in a new window]

Abstract

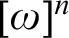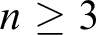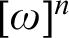Ramsey’s theorem asserts that every k-coloring of $[\omega ]^n$ admits an infinite monochromatic set. Whenever $n \geq 3$ , there exists a computable k-coloring of $[\omega ]^n$ whose solutions compute the halting set. On the other hand, for every computable k-coloring of 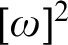$[\omega ]^2$ and every noncomputable set C, there is an infinite monochromatic set H such that 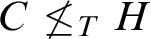$C \not \leq _T H$ . The latter property is known as cone avoidance.

In this article, we design a natural class of Ramsey-like theorems encompassing many statements studied in reverse mathematics. We prove that this class admits a maximal statement satisfying cone avoidance and use it as a criterion to re-obtain many existing proofs of cone avoidance. This maximal statement asserts the existence, for every k-coloring of 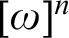$[\omega ]^n$ , of an infinite subdomain 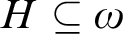$H \subseteq \omega $ over which the coloring depends only on the sparsity of its elements. This confirms the intuition that Ramsey-like theorems compute Turing degrees only through the sparsity of its solutions.

Keywords

Ramsey’s theoryreverse mathematicscomputability theorymodulus

MSC classification

Primary: 03B30: Foundations of classical theories (including reverse mathematics)
Secondary: 03D80: Applications of computability and recursion theory
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 1 , March 2022 , pp. 72 - 108
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bovykin, A. and Weiermann, A., The strength of infinitary Ramseyan principles can be accessed by their densities. Annals of Pure and Applied Logic , vol. 168 (2017), no. 9, pp. 1700–1709.10.1016/j.apal.2017.03.005CrossRefGoogle Scholar
Cholak, P. A., Giusto, M., Hirst, J. L., and Jockusch, C. G. Jr, Free sets and reverse mathematics . Reverse Mathematics , vol. 21 (2001), pp. 104–119.Google Scholar
Cholak, P. A., Jockusch, C. G., and Slaman, T. A., On the strength of Ramsey’s theorem for pairs , this Journal , vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
Cholak, P. A. and Patey, L., Thin set theorems and cone avoidance , Transactions of the American Mathematical Society . (2019). to appear.10.1090/tran/7987CrossRefGoogle Scholar
Chubb, J., Hirst, J. L., and McNicholl, T. H., Reverse mathematics, computability, and partitions of trees , this Journal , vol. 74 (2009), no. 1, pp. 201–215.Google Scholar
Csima, B. F., Hirschfeldt, D. R., Knight, J. F., and Soare, R. I., Bounding prime models , this Journal , vol. 69 (2004), pp. 1117–1142.Google Scholar
Csima, B. F. and Mileti, J. R., The strength of the rainbow Ramsey theorem , this Journal , vol. 74 (2009), no. 4, pp. 1310–1324.Google Scholar
Dorais, F. G., Dzhafarov, D. D., Hirst, J. L., Mileti, J. R., and Shafer, P., On uniform relationships between combinatorial problems . Transactions of the American Mathematical Society , vol. 368 (2016), no. 2, pp. 1321–1359.CrossRefGoogle Scholar
Dzhafarov, D. D. and Jockusch, C. G., Ramsey’s theorem and cone avoidance , this Journal , vol. 74 (2009), no. 2, pp. 557–578.Google Scholar
Dzhafarov, D. D. and Patey, L., Coloring trees in reverse mathematics . Advances in Mathematics , vol. 318 (2017), pp. 497–514.CrossRefGoogle Scholar
Friedman, H. M., Fom:53:free sets and reverse math and fom:54:recursion theory and dynamics, Available at https://www.cs.nyu.edu/pipermail/fom/.Google Scholar
Groszek, M. J. and Slaman, T. A., Moduli of Computation (talk) , Buenos Aires, Argentina, 2007.Google Scholar
Hirschfeldt, D. R. and Jockusch, C. G., On notions of computability-theoretic reduction between ${\varPi}_2^1$ principles . Journal of Mathematical Logic , vol. 16 (2016), no. 1, p. 1650002, 59.CrossRefGoogle Scholar
Hirschfeldt, D. R. and Shore, R. A., Combinatorial principles weaker than Ramsey’s theorem for pairs , this Journal , vol. 72 (2007), no. 1, pp. 171–206.Google Scholar
Jockusch, C. G., Ramsey’s theorem and recursion theory , this Journal , vol. 37 (1972), no. 2, pp. 268–280.Google Scholar
Lerman, M., Degrees of Unsolvability: Local and Global Theory. Perspectives in Mathematical Logic , Springer-Verlag, Berlin, 1983.10.1007/978-3-662-21755-9CrossRefGoogle Scholar
Liu, L., RT2 2 does not imply WKL0 , this Journal , vol. 77 (2012), no. 2, pp. 609–620.Google Scholar
Mileti, J. R., Partition theorems and computability theory , (Ph.D. thesis), University of Illinois at Urbana-Champaign, ProQuest LLC, Ann Arbor, MI, 2004.Google Scholar
Monin, B. and Patey, L., Pigeons do not jump high, to appear. 2018. Available at https://arxiv.org/abs/1803.09771.Google Scholar
Patey, L., Combinatorial weaknesses of Ramseyan principles, In preparation. 2015. Available at http://ludovicpatey.com/media/research/combinatorial-weaknesses-draft.pdf.Google Scholar
Patey, L., Iterative forcing and hyperimmunity in reverse mathematics , CiE. Evolving Computability (A. Beckmann, V. Mitrana, and M. Soskova, editors), Lecture Notes in Computer Science, vol. 9136, Springer International Publishing, Berlin, Germany, 2015, pp. 291–301 (English).10.1007/978-3-319-20028-6_30CrossRefGoogle Scholar
Patey, L., Somewhere over the rainbow Ramsey theorem for pairs, Submitted. 2015. Available at http://arxiv.org/abs/1501.07424.Google Scholar
Patey, L., Open questions about Ramsey-type statements in reverse mathematics . The Bulletin of Symbolic Logic , vol. 22 (2016), no. 2, pp. 151–169.CrossRefGoogle Scholar
Patey, L., The reverse mathematics of Ramsey-type theorems , Ph.D. thesis, Université Paris Diderot, 2016.Google Scholar
Patey, L., Iterative forcing and hyperimmunity in reverse mathematics . Computability , vol. 6 (2017), no. 3, pp. 209–221.CrossRefGoogle Scholar
Seetapun, D. and Slaman, T. A., On the strength of Ramsey’s theorem . Notre Dame Journal of Formal Logic , vol. 36 (1995), no. 4, pp. 570–582.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic , Cambridge University Press, Cambridge, MA, 2009.CrossRefGoogle Scholar
Solovay, R. M., Hyperarithmetically encodable sets . Transactions of the American Mathematica Society , vol. 239 (1978), pp. 99–122.CrossRefGoogle Scholar
Wang, W., Some logically weak Ramseyan theorems . Advances in Mathematics , vol. 261 (2014), pp. 1–25.CrossRefGoogle Scholar