Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-21T17:24:53.140Z Has data issue: false hasContentIssue false
  • English
  • Français

N-BERKELEY CARDINALS AND WEAK EXTENDER MODELS

Part of: Set theory

Published online by Cambridge University Press:  21 July 2020

RAFFAELLA CUTOLO
RAFFAELLA CUTOLO*
Affiliation:
DEPARTMENT OF MATHEMATICS AND APPLICATIONS UNIVERSITY OF NAPLES “FEDERICO II” VIA CINTIA 21, 80126NAPLES, ITALYE-mail: raffaella.cutolo@unina.it
Get access Rights & Permissions [Opens in a new window]

Abstract

For a given inner model N of ZFC, one can consider the relativized version of Berkeley cardinals in the context of ZFC, and ask if there can exist an “N-Berkeley cardinal.” In this article we provide a positive answer to this question. Indeed, under the assumption of a supercompact cardinal 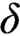$\delta $ , we show that there exists a ZFC inner model N such that there is a cardinal which is N-Berkeley, even in a strong sense. Further, the involved model N is a weak extender model of 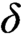$\delta $ is supercompact. Finally, we prove that the strong version of N-Berkeley cardinals turns out to be inconsistent whenever N satisfies closure under 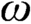$\omega $ -sequences.

Keywords

N-Berkeley cardinalsweak extender modelsHOD dichotomy

MSC classification

Primary: 03E45: Inner models, including constructibility, ordinal definability, and core models
Secondary: 03E55: Large cardinals
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 2 , June 2020 , pp. 809 - 816
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bagaria, J., Koellner, P., and Woodin, W. H., Large cardinals beyond Choice . The Bulletin of Symbolic Logic, vol. 25 (2019), pp. 283–318.CrossRefGoogle Scholar
Hamkins, J. D., Extensions with the approximation and cover properties have no new large cardinals . Fundamenta Mathematicae, vol. 180 (2003), pp. 257–277.CrossRefGoogle Scholar
Jech, T., Set Theory , third ed., Springer Monographs in Mathematics, Springer, Berlin, 2002.Google Scholar
Kanamori, A., The Higher Infinite: Large Cardinals in Set Theory from Their Beginnings , second ed., Springer Monographs in Mathematics, Springer, Berlin, 2003.Google Scholar
Woodin, W. H., Suitable extender models I . Journal of Mathematical Logic, vol. 10 (2010), pp. 101–339.CrossRefGoogle Scholar
Woodin, W. H., In search of Ultimate-L . The Bulletin of Symbolic Logic, vol. 23 (2017), pp. 1–109.CrossRefGoogle Scholar
Woodin, W. H., Davis, J., and Rodríguez, D., The HOD dichotomy, Appalachian Set Theory, 2006–2012 (Cummings, J. and Schimmerling, E., editors), London Mathematical Society Lecture Note Series, Cambridge University Press, Cambridge, 2012, pp. 397–419.CrossRefGoogle Scholar