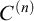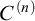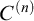We prove two general results about the preservation of extendible and $C^{(n)}$ -extendible cardinals under a wide class of forcing iterations (Theorems 5.4 and 7.5). As applications we give new proofs of the preservation of Vopěnka’s Principle and $C^{(n)}$ -extendible cardinals under Jensen’s iteration for forcing the GCH [17], previously obtained in [8, 27], respectively. We prove that $C^{(n)}$ -extendible cardinals are preserved by forcing with standard Easton-support iterations for any possible 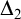$\Delta _2$ -definable behaviour of the power-set function on regular cardinals. We show that one can force proper class-many disagreements between the universe and HOD with respect to the calculation of successors of regular cardinals, while preserving 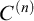$C^{(n)}$ -extendible cardinals. We also show, assuming the GCH, that the class forcing iteration of Cummings–Foreman–Magidor for forcing 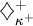$\diamondsuit _{\kappa ^+}^+$ at every 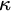$\kappa $ [10] preserves 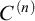$C^{(n)}$ -extendible cardinals. We give an optimal result on the consistency of weak square principles and $C^{(n)}$ -extendible cardinals. In the last section prove another preservation result for $C^{(n)}$ -extendible cardinals under very general (not necessarily definable or weakly homogeneous) class forcing iterations. 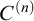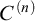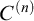As applications we prove the consistency of $C^{(n)}$ -extendible cardinals with 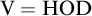$\mathrm {{V}}=\mathrm {{HOD}}$ , and also with 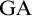$\mathrm {GA}$ (the Ground Axiom) plus 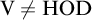$\mathrm {V}\neq \mathrm {HOD}$ , the latter being a strengthening of a result from [14].