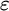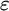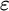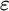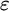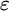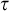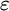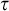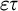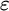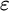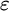1 Introduction
The
![]() $\varepsilon $
-calculus was originally introduced by Hilbert as a formalization of classical first-order logic. It is a way to reduce proofs in first-order logic to proofs in propositional logic from so-called critical formulas, where the role of quantifiers is taken over by certain terms. The
$\varepsilon $
-calculus was originally introduced by Hilbert as a formalization of classical first-order logic. It is a way to reduce proofs in first-order logic to proofs in propositional logic from so-called critical formulas, where the role of quantifiers is taken over by certain terms. The
![]() $\varepsilon $
-calculus was the basis for Hilbert’s approach to proof theory (in particular, consistency proofs). It still is a useful logical formalism with interesting properties and theoretical and practical applications.
$\varepsilon $
-calculus was the basis for Hilbert’s approach to proof theory (in particular, consistency proofs). It still is a useful logical formalism with interesting properties and theoretical and practical applications.
The
![]() $\varepsilon $
-calculus is formulated by allowing for terms of the form
$\varepsilon $
-calculus is formulated by allowing for terms of the form
![]() $\varepsilon _{x}\,A(x)$
for any formula
$\varepsilon _{x}\,A(x)$
for any formula
![]() $A(x)$
with x free. A formula of the form
$A(x)$
with x free. A formula of the form
![]() $A(t) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x))$
is called a critical formula belonging to
$A(t) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x))$
is called a critical formula belonging to
![]() $\varepsilon _{x}\,A(x)$
. A proof in the
$\varepsilon _{x}\,A(x)$
. A proof in the
![]() $\varepsilon $
-calculus is a proof in the quantifier-free fragment of classical logic from critical formulas. It is now possible to define the existential quantifier by
$\varepsilon $
-calculus is a proof in the quantifier-free fragment of classical logic from critical formulas. It is now possible to define the existential quantifier by
![]() $\exists x\, A(x) \equiv A(\varepsilon _{x}\,A(x))$
, and—in classical logic—the universal quantifier by
$\exists x\, A(x) \equiv A(\varepsilon _{x}\,A(x))$
, and—in classical logic—the universal quantifier by
![]() $\forall x\, A(x) \equiv A(\varepsilon _{x}\,\lnot A(x))$
. A formula A with quantifiers can thus be translated into a formula
$\forall x\, A(x) \equiv A(\varepsilon _{x}\,\lnot A(x))$
. A formula A with quantifiers can thus be translated into a formula
![]() $A^{\varepsilon }$
with
$A^{\varepsilon }$
with
![]() $\varepsilon $
-terms but without quantifiers. A formula is provable in classical first-order logic
$\varepsilon $
-terms but without quantifiers. A formula is provable in classical first-order logic
![]() $\mathbf {Q}\mathbf {C}$
iff its translation is provable in the
$\mathbf {Q}\mathbf {C}$
iff its translation is provable in the
![]() $\varepsilon $
-calculus.
$\varepsilon $
-calculus.
Hilbert proved two fundamental results about the
![]() $\varepsilon $
-calculus:
$\varepsilon $
-calculus:
-
1. The extended first
 $\varepsilon $
-theorem: If
$\varepsilon $
-theorem: If
 $A(\vec e)$
is derivable in the
$A(\vec e)$
is derivable in the
 $\varepsilon $
-calculus (
$\varepsilon $
-calculus (
 $\vec e$
a tuple of
$\vec e$
a tuple of
 $\varepsilon $
-terms), then there are tuples of terms
$\varepsilon $
-terms), then there are tuples of terms
 $\vec t_{1}, \dots , \vec t_{n}$
such that
$\vec t_{1}, \dots , \vec t_{n}$
such that
 $A(\vec t_{1}) \lor \cdots \lor A(\vec t_{n})$
is provable in propositional logic.
$A(\vec t_{1}) \lor \cdots \lor A(\vec t_{n})$
is provable in propositional logic. -
2. The second
 $\varepsilon $
-theorem: If
$\varepsilon $
-theorem: If
 $A^{\varepsilon }$
is the standard
$A^{\varepsilon }$
is the standard
 $\varepsilon $
-translation of a first-order formula derivable in the
$\varepsilon $
-translation of a first-order formula derivable in the
 $\varepsilon $
-calculus, A is derivable in first-order logic.
$\varepsilon $
-calculus, A is derivable in first-order logic.
The extended first
![]() $\varepsilon $
-theorem has two important consequences. The first consequence is what Hilbert simply called the first
$\varepsilon $
-theorem has two important consequences. The first consequence is what Hilbert simply called the first
![]() $\varepsilon $
-theorem: If A is
$\varepsilon $
-theorem: If A is
![]() $\varepsilon $
-free and derivable in the
$\varepsilon $
-free and derivable in the
![]() $\varepsilon $
-calculus, it is derivable in the quantifier-free fragment of first-order logic, the so-called elementary calculus of free variables (i.e., without critical formulas, indeed, without any use of
$\varepsilon $
-calculus, it is derivable in the quantifier-free fragment of first-order logic, the so-called elementary calculus of free variables (i.e., without critical formulas, indeed, without any use of
![]() $\varepsilon $
-terms). This implies that the
$\varepsilon $
-terms). This implies that the
![]() $\varepsilon $
-calculus is conservative over propositional logic for quantifier-free formulas without identity. The second consequence is Herbrand’s theorem for existential formulas: If
$\varepsilon $
-calculus is conservative over propositional logic for quantifier-free formulas without identity. The second consequence is Herbrand’s theorem for existential formulas: If
![]() $\exists \vec x\, A(\vec x)$
is provable in the
$\exists \vec x\, A(\vec x)$
is provable in the
![]() $\varepsilon $
-calculus, then some disjunction
$\varepsilon $
-calculus, then some disjunction
![]() $A(\vec t_{1}) \lor \cdots \lor A(\vec t_{n})$
is provable in propositional logic alone, i.e., is a tautology.Footnote
1
$A(\vec t_{1}) \lor \cdots \lor A(\vec t_{n})$
is provable in propositional logic alone, i.e., is a tautology.Footnote
1
In contrast to other proof-theoretic methods which also yield the existence of Herbrand disjunctions (such as cut-elimination), the proof based on the extended first
![]() $\varepsilon $
-theorem, and consequently the length of the Herbrand disjunction the proof yields, is insensitive to the propositional complexity of the original proof. This is an important advantage of methods based on the
$\varepsilon $
-theorem, and consequently the length of the Herbrand disjunction the proof yields, is insensitive to the propositional complexity of the original proof. This is an important advantage of methods based on the
![]() $\varepsilon $
-calculus.
$\varepsilon $
-calculus.
Hilbert’s results and proofs make essential use of classical principles, especially the law of excluded middle. The question naturally arises whether the results can also be obtained for weaker logics, and whether the same proof methods can be used, i.e., whether the use of excluded middle can be avoided. In this paper, we investigate
![]() $\varepsilon $
-calculi for intermediate logics, i.e., logics between intuitionistic and classical logic, and specifically the question of when the extended first
$\varepsilon $
-calculi for intermediate logics, i.e., logics between intuitionistic and classical logic, and specifically the question of when the extended first
![]() $\varepsilon $
-theorem holds in such logics. Well-known examples of intermediate logics are Jankov’s logic of weak excluded middle and finite- and infinite-valued Gödel–Dummett logics.
$\varepsilon $
-theorem holds in such logics. Well-known examples of intermediate logics are Jankov’s logic of weak excluded middle and finite- and infinite-valued Gödel–Dummett logics.
We consider only intermediate logics for two reasons. One is that Hilbert’s methods rely essentially on the deduction theorem, and this holds in intermediate logics but not in many other logics. The other is that
![]() $\varepsilon $
-calculi for intuitionistic and intermediate logics are of independent interest. What is the effect of adding
$\varepsilon $
-calculi for intuitionistic and intermediate logics are of independent interest. What is the effect of adding
![]() $\varepsilon $
-operators to intermediate logics? When does the extended first
$\varepsilon $
-operators to intermediate logics? When does the extended first
![]() $\varepsilon $
-theorem hold? When is the
$\varepsilon $
-theorem hold? When is the
![]() $\varepsilon $
-calculus for a logic conservative over the propositional base logic? We also, for the most part, discuss only pure logics, i.e., logics without identity.
$\varepsilon $
-calculus for a logic conservative over the propositional base logic? We also, for the most part, discuss only pure logics, i.e., logics without identity.
In intermediate logics it is necessary to introduce a separate
![]() $\tau $
-operator which defines the universal quantifier. Whereas
$\tau $
-operator which defines the universal quantifier. Whereas
![]() $A(\varepsilon _{x}\,A(x))$
translates
$A(\varepsilon _{x}\,A(x))$
translates
![]() $\exists x\,A(x)$
,
$\exists x\,A(x)$
,
![]() $A(\tau _{x}\,A(x))$
translates
$A(\tau _{x}\,A(x))$
translates
![]() $\forall x\,A(x)$
. The corresponding critical formulas are those of the form
$\forall x\,A(x)$
. The corresponding critical formulas are those of the form
![]() $A(\tau _{x}\,A(x)) \mathbin {\rightarrow } A(t)$
. Weakening the logic makes the addition of
$A(\tau _{x}\,A(x)) \mathbin {\rightarrow } A(t)$
. Weakening the logic makes the addition of
![]() $\tau $
necessary, since the equivalence of
$\tau $
necessary, since the equivalence of
![]() $\forall x\, A(x)$
and
$\forall x\, A(x)$
and
![]() $A(\varepsilon _{x}\,\lnot A(x))$
relies on the schema of contraposition; the equivalence of
$A(\varepsilon _{x}\,\lnot A(x))$
relies on the schema of contraposition; the equivalence of
![]() $\forall x\, A(x)$
and
$\forall x\, A(x)$
and
![]() $A(\tau _{x}\,A(x))$
does not. The system resulting from a propositional intermediate logic
$A(\tau _{x}\,A(x))$
does not. The system resulting from a propositional intermediate logic
![]() $\mathbf {L}$
by adding
$\mathbf {L}$
by adding
![]() $\varepsilon $
- and
$\varepsilon $
- and
![]() $\tau $
-terms and critical formulas is called the
$\tau $
-terms and critical formulas is called the
![]() ${\varepsilon \tau }$
-calculus for
${\varepsilon \tau }$
-calculus for
![]() $\mathbf {L}$
.
$\mathbf {L}$
.
It is well known that adding the
![]() $\varepsilon $
-operator to intuitionistic logic in a straightforward way results in translations
$\varepsilon $
-operator to intuitionistic logic in a straightforward way results in translations
![]() $A^{\varepsilon }$
of intuitionistically invalid formulas A becoming provable. Mints [Reference Mints20, Reference Mints and Petkov21] has investigated different systems based on intuitionistic logic with
$A^{\varepsilon }$
of intuitionistically invalid formulas A becoming provable. Mints [Reference Mints20, Reference Mints and Petkov21] has investigated different systems based on intuitionistic logic with
![]() $\varepsilon $
-operators which are conservative and in which the
$\varepsilon $
-operators which are conservative and in which the
![]() $\varepsilon $
-theorem holds. He allows the use of
$\varepsilon $
-theorem holds. He allows the use of
![]() $\varepsilon $
-terms only when
$\varepsilon $
-terms only when
![]() $\exists x\,A(x)$
has been established; other approaches (e.g., [Reference Shirai25]) use existence predicates to accomplish the same. We investigate the basic
$\exists x\,A(x)$
has been established; other approaches (e.g., [Reference Shirai25]) use existence predicates to accomplish the same. We investigate the basic
![]() ${\varepsilon \tau }$
-calculus without this assumption. In our
${\varepsilon \tau }$
-calculus without this assumption. In our
![]() ${\varepsilon \tau }$
-calculi,
${\varepsilon \tau }$
-calculi,
![]() ${\varepsilon \tau }$
-terms are treated syntactically as something like Skolem functions rather than semantically as choice operators.
${\varepsilon \tau }$
-terms are treated syntactically as something like Skolem functions rather than semantically as choice operators.
We begin (Section 2) by introducing intermediate logics. In Section 3 we introduce the
![]() ${\varepsilon \tau }$
-calculus and consider the differences in formulas provable in a logic vs. those provable in the corresponding
${\varepsilon \tau }$
-calculus and consider the differences in formulas provable in a logic vs. those provable in the corresponding
![]() ${\varepsilon \tau }$
-calculus. This is essentially the question of whether the addition of
${\varepsilon \tau }$
-calculus. This is essentially the question of whether the addition of
![]() $\varepsilon $
- and
$\varepsilon $
- and
![]() $\tau $
-terms and critical formulas allows the derivation (or requires the validity) of formulas not provable in the base logic.
$\tau $
-terms and critical formulas allows the derivation (or requires the validity) of formulas not provable in the base logic.
We investigate in detail which intuitionistically invalid formulas are provable in
![]() ${\varepsilon \tau }$
-calculi for intermediate logics in Section 4. We show that quantifier shift schemas play a special role here. All but three of these are valid in intuitionistic logic. The addition of
${\varepsilon \tau }$
-calculi for intermediate logics in Section 4. We show that quantifier shift schemas play a special role here. All but three of these are valid in intuitionistic logic. The addition of
![]() ${\varepsilon \tau }$
-terms and critical formulas results in the provability of the remaining three. Consequently, no intermediate first-order logic in which one of these three quantifier shifts is unprovable can have the second
${\varepsilon \tau }$
-terms and critical formulas results in the provability of the remaining three. Consequently, no intermediate first-order logic in which one of these three quantifier shifts is unprovable can have the second
![]() $\varepsilon $
-theorem (Proposition 4.1). This includes intuitionistic logic itself, logics complete for non-constant domain Kripke frames, and infinite-valued Gödel–Dummett logic.
$\varepsilon $
-theorem (Proposition 4.1). This includes intuitionistic logic itself, logics complete for non-constant domain Kripke frames, and infinite-valued Gödel–Dummett logic.
In Section 5, we show that conservativity for the propositional fragment nevertheless holds for all intermediate logics (Theorem 5.3). This in itself is a surprising result, even though the proof is very easy. It holds for theorems of the logics with or without identity, however not in general for provability from theories.
In Sections 6–9 we give a complete characterization of the intermediate logics where the extended first
![]() $\varepsilon $
-theorem holds. We show (Theorem 6.2) that whenever it holds, the underlying logic must prove (or validate) a sentence
$\varepsilon $
-theorem holds. We show (Theorem 6.2) that whenever it holds, the underlying logic must prove (or validate) a sentence
![]() ${B_{m}}$
of the form
${B_{m}}$
of the form
No
![]() $B_{m}$
is provable in intuitionistic logic, any logic complete for Kripke frames with branching worlds, or in infinite-valued Gödel–Dummett logic. Consequently, the extended first
$B_{m}$
is provable in intuitionistic logic, any logic complete for Kripke frames with branching worlds, or in infinite-valued Gödel–Dummett logic. Consequently, the extended first
![]() $\varepsilon $
-theorem does not hold for these logics.
$\varepsilon $
-theorem does not hold for these logics.
Provability of
![]() ${B_{m}}$
is also a sufficient condition: We show that the extended first
${B_{m}}$
is also a sufficient condition: We show that the extended first
![]() $\varepsilon $
-theorem holds whenever the underlying logic proves at least one
$\varepsilon $
-theorem holds whenever the underlying logic proves at least one
![]() ${B_{m}}$
. The argument follows the idea of Hilbert’s proof, but does not make use of excluded middle. In order to establish the result, we provide a more fine-grained analysis of the proof of the extended first
${B_{m}}$
. The argument follows the idea of Hilbert’s proof, but does not make use of excluded middle. In order to establish the result, we provide a more fine-grained analysis of the proof of the extended first
![]() $\varepsilon $
-theorem. We first introduce the notion of an elimination set in Section 7: a set of terms which can replace an
$\varepsilon $
-theorem. We first introduce the notion of an elimination set in Section 7: a set of terms which can replace an
![]() $\varepsilon $
-term in a proof and render the corresponding critical formulas redundant, using only the resources of the underlying propositional logic. This is the part of Hilbert’s proof that uses excluded middle. We isolate here how excluded middle is used. In Section 8, we show that logics that prove some
$\varepsilon $
-term in a proof and render the corresponding critical formulas redundant, using only the resources of the underlying propositional logic. This is the part of Hilbert’s proof that uses excluded middle. We isolate here how excluded middle is used. In Section 8, we show that logics that prove some
![]() ${B_{m}}$
also have elimination sets.
${B_{m}}$
also have elimination sets.
If such elimination sets exist, the procedure given by Hilbert and Bernays can be used for a proof of the extended first
![]() $\varepsilon $
-theorem (Section 9). This establishes the second half of the characterization, that the extended first
$\varepsilon $
-theorem (Section 9). This establishes the second half of the characterization, that the extended first
![]() ${\varepsilon \tau }$
-theorem holds in logics that prove
${\varepsilon \tau }$
-theorem holds in logics that prove
![]() ${B_{m}}$
, i.e., the finite-valued Gödel logics (Theorem 9.9). By putting emphasis on elimination sets, we can also show that in logics in which the extended first
${B_{m}}$
, i.e., the finite-valued Gödel logics (Theorem 9.9). By putting emphasis on elimination sets, we can also show that in logics in which the extended first
![]() $\varepsilon $
-theorem does not hold in general, it may still hold for formulas of a special form. This allows us to show that the extended first
$\varepsilon $
-theorem does not hold in general, it may still hold for formulas of a special form. This allows us to show that the extended first
![]() ${\varepsilon \tau }$
-theorem holds for negated formulas in Jankov’s logic of weak excluded middle (Theorem 9.8). We also show that the first
${\varepsilon \tau }$
-theorem holds for negated formulas in Jankov’s logic of weak excluded middle (Theorem 9.8). We also show that the first
![]() ${\varepsilon \tau }$
-theorem (for theorems not containing
${\varepsilon \tau }$
-theorem (for theorems not containing
![]() ${\varepsilon \tau }$
-terms) holds for infinite-valued Gödel–Dummett logic (Theorem 9.10).
${\varepsilon \tau }$
-terms) holds for infinite-valued Gödel–Dummett logic (Theorem 9.10).
The extended first
![]() ${\varepsilon \tau }$
-theorem is closely related to Herbrand’s theorem. We discuss this connection, as well as the second
${\varepsilon \tau }$
-theorem is closely related to Herbrand’s theorem. We discuss this connection, as well as the second
![]() ${\varepsilon \tau }$
-theorem, in Section 10. We show that the second
${\varepsilon \tau }$
-theorem, in Section 10. We show that the second
![]() ${\varepsilon \tau }$
-theorem holds for any intermediate predicate logic that proves all quantifier shifts and has the extended first
${\varepsilon \tau }$
-theorem holds for any intermediate predicate logic that proves all quantifier shifts and has the extended first
![]() ${\varepsilon \tau }$
-theorem (Proposition 10.2), e.g.,
${\varepsilon \tau }$
-theorem (Proposition 10.2), e.g.,
![]() $\mathbf {Q}\mathbf {LC}_{m} + \mathit {CD}$
, first-order finite-valued Gödel logic.
$\mathbf {Q}\mathbf {LC}_{m} + \mathit {CD}$
, first-order finite-valued Gödel logic.
In the case of some proofs, it is possible to eliminate
![]() ${\varepsilon \tau }$
-terms in a simplified way where the cases that require the presence of
${\varepsilon \tau }$
-terms in a simplified way where the cases that require the presence of
![]() ${B_{m}}$
do not arise, and the linearity schema
${B_{m}}$
do not arise, and the linearity schema
![]() $\mathit {Lin}$
(
$\mathit {Lin}$
(
![]() $(A \mathbin {\rightarrow } B) \lor (B \mathbin {\rightarrow } A)$
) is enough. Although we cannot give an independent characterization of the proofs or theorems for which this is the case, the simplified procedure will sometimes terminate and produce a Herbrand disjunction. Conversely, if a Herbrand disjunction exists, there is always a proof of the original formula for which the procedure terminates and produces the Herbrand disjunction (Section 11).
$(A \mathbin {\rightarrow } B) \lor (B \mathbin {\rightarrow } A)$
) is enough. Although we cannot give an independent characterization of the proofs or theorems for which this is the case, the simplified procedure will sometimes terminate and produce a Herbrand disjunction. Conversely, if a Herbrand disjunction exists, there is always a proof of the original formula for which the procedure terminates and produces the Herbrand disjunction (Section 11).
This result sheds light on the conditions under which (a version of) Hilbert’s method which uses principles weaker than excluded middle produces a Herbrand disjunction. In fact, a similar method can be used to give a partial
![]() $\varepsilon $
-elimination procedure for number theory, where linearity of the natural order of
$\varepsilon $
-elimination procedure for number theory, where linearity of the natural order of
![]() $\mathbb {N}$
plays a similar role as the schema of linearity does in the case of logic (Section 12). We summarize the logics considered and results established in Tables 1 and 2.
$\mathbb {N}$
plays a similar role as the schema of linearity does in the case of logic (Section 12). We summarize the logics considered and results established in Tables 1 and 2.
Table 1 Intermediate logics considered.

Table 2 Epsilon theorems for intermediate logics.

2 Preliminaries
Intermediate propositional logics have been investigated extensively since the 1950s. Intermediate predicate logics are comparatively less well understood; however, they constitute an active area of research (see [Reference Gabbay, Shehtman and Skvortsov14]). We begin by collecting some preliminary definitions.
All the logics we consider are formulated in the standard language of intuitionistic and classical logic with propositional connectives
![]() $\land $
,
$\land $
,
![]() $\lor $
,
$\lor $
,
![]() $\mathbin {\rightarrow }$
, the constant
$\mathbin {\rightarrow }$
, the constant
![]() $\bot $
for absurdity, and the quantifiers
$\bot $
for absurdity, and the quantifiers
![]() $\forall $
and
$\forall $
and
![]() $\exists $
.
$\exists $
.
![]() $\lnot A$
is defined as
$\lnot A$
is defined as
![]() $A \mathbin {\rightarrow } \bot $
and
$A \mathbin {\rightarrow } \bot $
and
![]() $\top $
as
$\top $
as
![]() $\lnot \bot $
. Terms and atomic formulas are defined as usual. We allow
$\lnot \bot $
. Terms and atomic formulas are defined as usual. We allow
![]() $0$
-place predicate symbols, i.e., propositional variables. A formula containing no quantifiers is called quantifier-free and a quantifier-free formula with only
$0$
-place predicate symbols, i.e., propositional variables. A formula containing no quantifiers is called quantifier-free and a quantifier-free formula with only
![]() $0$
-place predicate symbols is called propositional. For the most part we will consider pure logics, i.e., logics not involving the identity predicate
$0$
-place predicate symbols is called propositional. For the most part we will consider pure logics, i.e., logics not involving the identity predicate
![]() $=$
. We assume that function symbols are available, however.
$=$
. We assume that function symbols are available, however.
We use A, B, …, as metavariables for formulas, and t, s, …, as metavariables for terms. We write
![]() $A(x)$
to indicate that x occurs free in A. The result of substituting s for all (free) occurrences of x in a term t or a formula A is indicated by
$A(x)$
to indicate that x occurs free in A. The result of substituting s for all (free) occurrences of x in a term t or a formula A is indicated by
![]() $t[s/x]$
or
$t[s/x]$
or
![]() $A[s/x]$
. When it is clear which variable x is intended, we write
$A[s/x]$
. When it is clear which variable x is intended, we write
![]() $A(s)$
for
$A(s)$
for
![]() $A[s/x]$
. The result of replacing every occurrence of a term t by a term s in a formula A is indicated by
$A[s/x]$
. The result of replacing every occurrence of a term t by a term s in a formula A is indicated by
![]() $A[s/t]$
. A substitution instance of a formula A is any formula resulting from A by uniformly replacing any number of atomic formulas
$A[s/t]$
. A substitution instance of a formula A is any formula resulting from A by uniformly replacing any number of atomic formulas
![]() $P(t_{1}, \dots , t_{n})$
by formulas
$P(t_{1}, \dots , t_{n})$
by formulas
![]() $B[t_{1}/x_{1}, \dots , t_{n}/x_{n}]$
(in such a way that free variables of B are not captured by quantifiers in A of course). In particular, a substitution instance of a propositional formula A is any formula resulting from A by uniformly replacing any number of
$B[t_{1}/x_{1}, \dots , t_{n}/x_{n}]$
(in such a way that free variables of B are not captured by quantifiers in A of course). In particular, a substitution instance of a propositional formula A is any formula resulting from A by uniformly replacing any number of
![]() $0$
-place predicate symbols P by formulas B.
$0$
-place predicate symbols P by formulas B.
Definition 2.1. A propositional logic
![]() $\mathbf {L}$
is a set of propositional formulas closed under substitution and modus ponens, i.e., if
$\mathbf {L}$
is a set of propositional formulas closed under substitution and modus ponens, i.e., if
![]() $\mathbf {L}$
contains
$\mathbf {L}$
contains
![]() $A \mathbin {\rightarrow } B$
and B it also contains B. A predicate logic is a set of formulas closed under substitution, modus ponens, and the quantifier rules
$A \mathbin {\rightarrow } B$
and B it also contains B. A predicate logic is a set of formulas closed under substitution, modus ponens, and the quantifier rules

which are subject to the eigenvariable condition: x must not be free in the conclusion.
Logics can be characterized by the formulas derivable from a set of axiom schemas by modus ponens. This is of course equivalent to closing the axioms under substitution and modus ponens. For instance, intuitionistic propositional logic
![]() $\mathbf {H}$
is obtained from the propositional axioms given in [Reference Troelstra and van Dalen28, 4.1]. Classical propositional logic
$\mathbf {H}$
is obtained from the propositional axioms given in [Reference Troelstra and van Dalen28, 4.1]. Classical propositional logic
![]() $\mathbf {C}$
and predicate logic
$\mathbf {C}$
and predicate logic
![]() $\mathbf {Q}\mathbf {C}$
are obtained by adding
$\mathbf {Q}\mathbf {C}$
are obtained by adding
![]() $\lnot A \lor A$
(or alternatively
$\lnot A \lor A$
(or alternatively
![]() $\lnot \lnot A \mathbin {\rightarrow } A$
) as an axiom.
$\lnot \lnot A \mathbin {\rightarrow } A$
) as an axiom.
Definition 2.2. An intermediate propositional logic
![]() $\mathbf {L}$
is a propositional logic that contains
$\mathbf {L}$
is a propositional logic that contains
![]() $\mathbf {H}$
and is contained in
$\mathbf {H}$
and is contained in
![]() $\mathbf {C}$
.
$\mathbf {C}$
.
The following intermediate propositional logics will play important roles:
-
1.
 $\mathbf {LC}$
, characterized alternatively as the formulas valid on linearly ordered Kripke frames or as infinite-valued Gödel logic,Footnote
2
axiomatized over
$\mathbf {LC}$
, characterized alternatively as the formulas valid on linearly ordered Kripke frames or as infinite-valued Gödel logic,Footnote
2
axiomatized over
 $\mathbf {H}{}$
using the schema (Lin)
$\mathbf {H}{}$
using the schema (Lin) $$\begin{align} (A \mathbin{\rightarrow} B) \lor (B \mathbin{\rightarrow} A). \end{align}$$
$$\begin{align} (A \mathbin{\rightarrow} B) \lor (B \mathbin{\rightarrow} A). \end{align}$$
-
2.
 $\mathbf {LC}_{m} = \mathbf {LC} + {B_{m}}$
, characterized as formulas valid on linearly ordered Kripke frames of height
$\mathbf {LC}_{m} = \mathbf {LC} + {B_{m}}$
, characterized as formulas valid on linearly ordered Kripke frames of height
 $< m$
, or as the Gödel logic on m truth values, also known as
$< m$
, or as the Gödel logic on m truth values, also known as
 $\textbf {S}_{m-1}$
[Reference Hosoi16]. Here,
$\textbf {S}_{m-1}$
[Reference Hosoi16]. Here,
 ${B_{m}}$
is: (Bm)
${B_{m}}$
is: (Bm) $$\begin{align} (A_{1} \mathbin{\rightarrow} A_{2}) \lor (A_{2} \mathbin{\rightarrow} A_{3}) \lor \dots \lor (A_{m} \mathbin{\rightarrow} A_{m+1}). \end{align}$$
$$\begin{align} (A_{1} \mathbin{\rightarrow} A_{2}) \lor (A_{2} \mathbin{\rightarrow} A_{3}) \lor \dots \lor (A_{m} \mathbin{\rightarrow} A_{m+1}). \end{align}$$
-
3.
 $\mathbf {KC}$
, the logic of weak excluded middle [Reference Jankov19], axiomatized over
$\mathbf {KC}$
, the logic of weak excluded middle [Reference Jankov19], axiomatized over
 $\mathbf {H}{}$
using the schema (J)
$\mathbf {H}{}$
using the schema (J) $$\begin{align} \lnot A \lor \lnot\lnot A. \end{align}$$
$$\begin{align} \lnot A \lor \lnot\lnot A. \end{align}$$
If
![]() $\mathbf {L}$
is an intermediate propositional logic, we can consider the corresponding “elementary calculus,” i.e., the system obtained by replacing propositional variables with atomic formulas of a first-order language, with or without identity. We will be interested in formulas provable in such an elementary calculus from a set of assumptions
$\mathbf {L}$
is an intermediate propositional logic, we can consider the corresponding “elementary calculus,” i.e., the system obtained by replacing propositional variables with atomic formulas of a first-order language, with or without identity. We will be interested in formulas provable in such an elementary calculus from a set of assumptions
![]() $\Gamma $
.
$\Gamma $
.
Definition 2.3. Suppose
![]() $\mathbf {L}$
is an intermediate logic. A proof
$\mathbf {L}$
is an intermediate logic. A proof
![]() $\pi $
of A from
$\pi $
of A from
![]() $\Gamma $
in the corresponding elementary calculus is a sequence
$\Gamma $
in the corresponding elementary calculus is a sequence
![]() $A_{1}$
, …,
$A_{1}$
, …,
![]() $A_{n} =A$
of quantifier-free formulas such that each
$A_{n} =A$
of quantifier-free formulas such that each
![]() $A_{i}$
is either a substitution instance of a formula in
$A_{i}$
is either a substitution instance of a formula in
![]() $\mathbf {L}$
, is in
$\mathbf {L}$
, is in
![]() $\Gamma $
, or follows from formulas
$\Gamma $
, or follows from formulas
![]() $A_{k}$
and
$A_{k}$
and
![]() $A_{l}$
(
$A_{l}$
(
![]() $k, l < i$
) by modus ponens, and
$k, l < i$
) by modus ponens, and
![]() $A_{n} \equiv A$
. We then write
$A_{n} \equiv A$
. We then write
![]() $\Gamma \vdash _{\mathbf {L}}^{\pi } A$
. If such a proof
$\Gamma \vdash _{\mathbf {L}}^{\pi } A$
. If such a proof
![]() $\pi $
exists we write
$\pi $
exists we write
![]() $\Gamma \vdash _{\mathbf {L}}$
and if
$\Gamma \vdash _{\mathbf {L}}$
and if
![]() $\Gamma $
is empty, simply
$\Gamma $
is empty, simply
![]() $\mathbf {L} \vdash A$
. If
$\mathbf {L} \vdash A$
. If
![]() $\mathbf {L}$
is not mentioned, we mean
$\mathbf {L}$
is not mentioned, we mean
![]() $\mathbf {H}$
.
$\mathbf {H}$
.
Given a propositional logic
![]() $\mathbf {L}$
, and possibly a set of additional axiom schemas
$\mathbf {L}$
, and possibly a set of additional axiom schemas
![]() $\mathit {Ax}$
involving quantifiers, we can generate a predicate logic:
$\mathit {Ax}$
involving quantifiers, we can generate a predicate logic:
Definition 2.4. If
![]() $\mathbf {L}$
is a propositional logic, and
$\mathbf {L}$
is a propositional logic, and
![]() $\mathit {Ax}$
is a set of formulas, then
$\mathit {Ax}$
is a set of formulas, then
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is the smallest predicate logic containing
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is the smallest predicate logic containing
![]() $\mathbf {L}$
, the standard quantifier axioms
$\mathbf {L}$
, the standard quantifier axioms
 $$ \begin{align*} \forall x\, A(x) & \mathbin{\rightarrow} A(t) \quad \text{and}\\ A(t) & \mathbin{\rightarrow} \exists x\, A(x), \end{align*} $$
$$ \begin{align*} \forall x\, A(x) & \mathbin{\rightarrow} A(t) \quad \text{and}\\ A(t) & \mathbin{\rightarrow} \exists x\, A(x), \end{align*} $$
and the formulas in
![]() $\mathit {Ax}$
.
$\mathit {Ax}$
.
If
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
contains intuitionistic predicate logic
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
contains intuitionistic predicate logic
![]() $\mathbf {Q}\mathbf {H}$
and is contained in classical predicate logic
$\mathbf {Q}\mathbf {H}$
and is contained in classical predicate logic
![]() $\mathbf {Q}\mathbf {C}$
, it is called an intermediate predicate logic.
$\mathbf {Q}\mathbf {C}$
, it is called an intermediate predicate logic.
Definition 2.5. Suppose
![]() $\mathbf {L}$
is a propositional logic. A proof
$\mathbf {L}$
is a propositional logic. A proof
![]() $\pi $
of A in
$\pi $
of A in
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is a sequence
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is a sequence
![]() $A_{1}$
, …,
$A_{1}$
, …,
![]() $A_{n} = A$
of formulas of predicate logic such that each
$A_{n} = A$
of formulas of predicate logic such that each
![]() $A_{i}$
is either a substitution instance of a formula in
$A_{i}$
is either a substitution instance of a formula in
![]() $\mathbf {L}$
, of a standard quantifier axiom, of a formula in
$\mathbf {L}$
, of a standard quantifier axiom, of a formula in
![]() $\mathit {Ax}$
, or follows from previous formulas by modus ponens or a quantifier rule. We then write
$\mathit {Ax}$
, or follows from previous formulas by modus ponens or a quantifier rule. We then write
![]() $ \mathbf {Q}\mathbf {L} + \mathit {Ax} \vdash ^{\pi } A$
. If such a proof
$ \mathbf {Q}\mathbf {L} + \mathit {Ax} \vdash ^{\pi } A$
. If such a proof
![]() $\pi $
exists we write
$\pi $
exists we write
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax} \vdash A$
.
$\mathbf {Q}\mathbf {L} + \mathit {Ax} \vdash A$
.
A is a formula in
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
iff
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
iff
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax} \vdash A$
. If
$\mathbf {Q}\mathbf {L} + \mathit {Ax} \vdash A$
. If
![]() $\mathbf {L}{}$
itself is characterized by a set of propositional axioms, it is enough to require substitution instances of axioms of
$\mathbf {L}{}$
itself is characterized by a set of propositional axioms, it is enough to require substitution instances of axioms of
![]() $\mathbf {L}{}$
in the above definition. For instance, taking
$\mathbf {L}{}$
in the above definition. For instance, taking
![]() $\mathbf {H}{}$
as above, the proofs in intuitionistic predicate logic
$\mathbf {H}{}$
as above, the proofs in intuitionistic predicate logic
![]() $\mathbf {Q}\mathbf {H}$
are just the proofs in the system
$\mathbf {Q}\mathbf {H}$
are just the proofs in the system
![]() $H_{2}$
-IQC of [Reference Troelstra and van Dalen28, 4.3].
$H_{2}$
-IQC of [Reference Troelstra and van Dalen28, 4.3].
If
![]() $\mathit {Ax}$
is empty,
$\mathit {Ax}$
is empty,
![]() $\mathbf {Q}\mathbf {L} = \mathbf {Q}\mathbf {L} + \mathit {Ax}$
is the weakest pure intermediate predicate logic extending
$\mathbf {Q}\mathbf {L} = \mathbf {Q}\mathbf {L} + \mathit {Ax}$
is the weakest pure intermediate predicate logic extending
![]() $\mathbf {L}$
. For instance,
$\mathbf {L}$
. For instance,
![]() $\mathbf {Q}\mathbf {LC}$
is the weakest predicate logic obtained from
$\mathbf {Q}\mathbf {LC}$
is the weakest predicate logic obtained from
![]() $\mathbf {LC}$
, and is axiomatized by
$\mathbf {LC}$
, and is axiomatized by
![]() $\mathbf {Q}\mathbf {H} + \mathit {Lin}$
. It is complete for linearly ordered Kripke frames (see [Reference Corsi11, Reference Skvortsov26]).
$\mathbf {Q}\mathbf {H} + \mathit {Lin}$
. It is complete for linearly ordered Kripke frames (see [Reference Corsi11, Reference Skvortsov26]).
It is possible to extend the weakest predicate logic of an intermediate propositional logic
![]() $\mathbf {L}$
by adding intuitionistically invalid schemas
$\mathbf {L}$
by adding intuitionistically invalid schemas
![]() $\mathit {Ax}$
involving quantifiers. Some important examples are the constant domain principle,
$\mathit {Ax}$
involving quantifiers. Some important examples are the constant domain principle,
the double negation shift (or Kuroda’s principle),
and the quantifier shifts
![]() $\mathbf {Q}\mathbf {LC} + \mathit {CD}$
axiomatizes the formulas valid on linearly ordered Kripke frames with constant domains, and also the first-order Gödel logic
$\mathbf {Q}\mathbf {LC} + \mathit {CD}$
axiomatizes the formulas valid on linearly ordered Kripke frames with constant domains, and also the first-order Gödel logic
![]() $\mathbf {G}_{\mathbb {R}}$
of formulas valid on the interval
$\mathbf {G}_{\mathbb {R}}$
of formulas valid on the interval
![]() $[0, 1]$
.
$[0, 1]$
.
![]() $\mathbf {Q}\mathbf {H} + K$
characterizes the formulas valid on Kripke frames with the McKinsey property and
$\mathbf {Q}\mathbf {H} + K$
characterizes the formulas valid on Kripke frames with the McKinsey property and
![]() $\mathbf {Q}\mathbf {LC} + \mathit {CD} + K$
is the logic of linear Kripke frames with maximal element. It is also the first-order Gödel logic
$\mathbf {Q}\mathbf {LC} + \mathit {CD} + K$
is the logic of linear Kripke frames with maximal element. It is also the first-order Gödel logic
![]() $\mathbf {G}_{0}$
of formulas valid on
$\mathbf {G}_{0}$
of formulas valid on
![]() $\{0\} \cup [1/2,1]$
.
$\{0\} \cup [1/2,1]$
.
![]() $\mathbf {Q}\mathbf {LC}_{m}$
is not complete for linear Kripke frames of height
$\mathbf {Q}\mathbf {LC}_{m}$
is not complete for linear Kripke frames of height
![]() $< m$
(contrary to what one might expect). However,
$< m$
(contrary to what one might expect). However,
![]() $\mathbf {G}_{m} = \mathbf {Q}\mathbf {LC}_{m} + \mathit {CD}$
is complete for linearly ordered Kripke frames of height
$\mathbf {G}_{m} = \mathbf {Q}\mathbf {LC}_{m} + \mathit {CD}$
is complete for linearly ordered Kripke frames of height
![]() $<m$
with constant domains. It is also the m-valued first-order Gödel logic
$<m$
with constant domains. It is also the m-valued first-order Gödel logic
![]() $\mathbf {G}_{m}$
.Footnote
3
$\mathbf {G}_{m}$
.Footnote
3
3
 ${\varepsilon \tau }$
-calculi for intermediate logics
${\varepsilon \tau }$
-calculi for intermediate logics
Formulas and terms of the
![]() ${\varepsilon \tau }$
-calculus are defined by simultaneous induction, allowing that if
${\varepsilon \tau }$
-calculus are defined by simultaneous induction, allowing that if
![]() $A(x)$
is a formula already defined, then
$A(x)$
is a formula already defined, then
![]() $\varepsilon _{x}\,A(x)$
and
$\varepsilon _{x}\,A(x)$
and
![]() $\tau _{x}\,A(x)$
are terms. In
$\tau _{x}\,A(x)$
are terms. In
![]() $\varepsilon _{x}\,A(x)$
and
$\varepsilon _{x}\,A(x)$
and
![]() $\tau _{x}\,A(x)$
the variable x is bound. We call terms of the form
$\tau _{x}\,A(x)$
the variable x is bound. We call terms of the form
![]() $\varepsilon _{x}\,A(x)\ \varepsilon $
-terms and those of the form
$\varepsilon _{x}\,A(x)\ \varepsilon $
-terms and those of the form
![]() $\tau _{x}\,A(x)\ \tau $
-terms (collectively:
$\tau _{x}\,A(x)\ \tau $
-terms (collectively:
![]() ${\varepsilon \tau }$
-terms).
${\varepsilon \tau }$
-terms).
As usual, we consider
![]() $\varepsilon $
- and
$\varepsilon $
- and
![]() $\tau $
-terms to be identical up to renaming of bound variables, and define substitution of
$\tau $
-terms to be identical up to renaming of bound variables, and define substitution of
![]() ${\varepsilon \tau }$
-terms into formulas, as in
${\varepsilon \tau }$
-terms into formulas, as in
![]() $A(\varepsilon _{x}\,A(x))$
, so that bound variables are tacitly renamed to avoid clashes.
$A(\varepsilon _{x}\,A(x))$
, so that bound variables are tacitly renamed to avoid clashes.
Definition 3.1. A critical formula belonging to
![]() $\varepsilon _{x}\,A(x)$
is any formula of the form
$\varepsilon _{x}\,A(x)$
is any formula of the form
![]() $A(t) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x))$
.
$A(t) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x))$
.
A critical formula belonging to
![]() $\tau _{x}\,A(x)$
is any formula of the form
$\tau _{x}\,A(x)$
is any formula of the form
![]() $A(\tau _{x}\,A(x)) \mathbin {\rightarrow } A(t)$
.
$A(\tau _{x}\,A(x)) \mathbin {\rightarrow } A(t)$
.
Definition 3.2. Suppose
![]() $\mathbf {L}$
is an intermediate propositional logic. An
$\mathbf {L}$
is an intermediate propositional logic. An
![]() ${\varepsilon \tau }$
-proof
${\varepsilon \tau }$
-proof
![]() $\pi $
of B is a proof in the elementary calculus of
$\pi $
of B is a proof in the elementary calculus of
![]() $\mathbf {L}$
from critical formulas
$\mathbf {L}$
from critical formulas
![]() $\Gamma $
of the form
$\Gamma $
of the form
 $$ \begin{align*} A(t) & \mathbin{\rightarrow} A(\varepsilon_{x}\,A(x)),\\ A(\tau_{x}\,A(x)) & \mathbin{\rightarrow} A(t). \end{align*} $$
$$ \begin{align*} A(t) & \mathbin{\rightarrow} A(\varepsilon_{x}\,A(x)),\\ A(\tau_{x}\,A(x)) & \mathbin{\rightarrow} A(t). \end{align*} $$
We write
![]() $\mathbf {L}{\varepsilon \tau } \vdash B$
if such a
$\mathbf {L}{\varepsilon \tau } \vdash B$
if such a
![]() $\pi $
exists, or
$\pi $
exists, or
![]() $\Gamma \vdash _{\mathbf {L}{\varepsilon \tau }}^{\pi } B$
when we want to identify the critical formulas and the proof
$\Gamma \vdash _{\mathbf {L}{\varepsilon \tau }}^{\pi } B$
when we want to identify the critical formulas and the proof
![]() $\pi $
.
$\pi $
.
The pure
![]() ${\varepsilon \tau }$
-calculus
${\varepsilon \tau }$
-calculus
![]() $\mathbf {L}{\varepsilon \tau }$
of
$\mathbf {L}{\varepsilon \tau }$
of
![]() $\mathbf {L}$
is the set of quantifier-free formulas that have
$\mathbf {L}$
is the set of quantifier-free formulas that have
![]() ${\varepsilon \tau }$
-proofs.
${\varepsilon \tau }$
-proofs.
We are interested in the relationships between intermediate predicate logics
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
and the
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
and the
![]() ${\varepsilon \tau }$
-calculus
${\varepsilon \tau }$
-calculus
![]() $\mathbf {L}{\varepsilon \tau }$
of their propositional fragment
$\mathbf {L}{\varepsilon \tau }$
of their propositional fragment
![]() $\mathbf {L}$
. Since the language of
$\mathbf {L}$
. Since the language of
![]() $\mathbf {L}{\varepsilon \tau }$
does not contain quantifiers, we must define a translation of predicate formulas that do contain them into the language of the
$\mathbf {L}{\varepsilon \tau }$
does not contain quantifiers, we must define a translation of predicate formulas that do contain them into the language of the
![]() ${\varepsilon \tau }$
-calculus.
${\varepsilon \tau }$
-calculus.
Definition 3.3. The
![]() ${\varepsilon \tau }$
-translation
${\varepsilon \tau }$
-translation
![]() $A^{\varepsilon \tau }$
of a formula A is defined as follows:
$A^{\varepsilon \tau }$
of a formula A is defined as follows:
 $$ \begin{align*} A^{\varepsilon\tau} & = A \text{ if }A\text{ is atomic}.\\ (A \land B)^{\varepsilon\tau} & = A^{\varepsilon\tau} \land B^{\varepsilon\tau}, & (A \lor B)^{\varepsilon\tau} & = A^{\varepsilon\tau} \lor B^{\varepsilon\tau}, \\ (A \mathbin{\rightarrow} B)^{\varepsilon\tau} & = A^{\varepsilon\tau} \mathbin{\rightarrow} B^{\varepsilon\tau}, & (\lnot A)^{\varepsilon\tau} & = \lnot A^{\varepsilon\tau}, \\ (\exists x\, A(x))^{\varepsilon\tau} & = A^{\varepsilon\tau}(\varepsilon_{x}\,A(x)^{\varepsilon\tau}), & (\forall x\, A(x))^{\varepsilon\tau} & = A^{\varepsilon\tau}(\tau_{x}\,A(x)^{\varepsilon\tau}). \end{align*} $$
$$ \begin{align*} A^{\varepsilon\tau} & = A \text{ if }A\text{ is atomic}.\\ (A \land B)^{\varepsilon\tau} & = A^{\varepsilon\tau} \land B^{\varepsilon\tau}, & (A \lor B)^{\varepsilon\tau} & = A^{\varepsilon\tau} \lor B^{\varepsilon\tau}, \\ (A \mathbin{\rightarrow} B)^{\varepsilon\tau} & = A^{\varepsilon\tau} \mathbin{\rightarrow} B^{\varepsilon\tau}, & (\lnot A)^{\varepsilon\tau} & = \lnot A^{\varepsilon\tau}, \\ (\exists x\, A(x))^{\varepsilon\tau} & = A^{\varepsilon\tau}(\varepsilon_{x}\,A(x)^{\varepsilon\tau}), & (\forall x\, A(x))^{\varepsilon\tau} & = A^{\varepsilon\tau}(\tau_{x}\,A(x)^{\varepsilon\tau}). \end{align*} $$
Again, substitution of
![]() ${\varepsilon \tau }$
-terms for variables must be understood modulo renaming of bound variables so as to avoid clashes. Clearly, if A contains no quantifiers, then
${\varepsilon \tau }$
-terms for variables must be understood modulo renaming of bound variables so as to avoid clashes. Clearly, if A contains no quantifiers, then
![]() $A^{\varepsilon \tau } = A$
.
$A^{\varepsilon \tau } = A$
.
The point of the classical
![]() $\varepsilon $
-calculus is that it can replace quantifiers and quantifier inferences. And indeed, in classical first-order logic, a first-order formula A is provable iff its translation
$\varepsilon $
-calculus is that it can replace quantifiers and quantifier inferences. And indeed, in classical first-order logic, a first-order formula A is provable iff its translation
![]() $A^{\varepsilon }$
is provable in the pure
$A^{\varepsilon }$
is provable in the pure
![]() $\varepsilon $
-calculus. The “if” direction is the content of the second
$\varepsilon $
-calculus. The “if” direction is the content of the second
![]() $\varepsilon $
-theorem, while the “only if” direction follows more simply by translating derivations.
$\varepsilon $
-theorem, while the “only if” direction follows more simply by translating derivations.
We defined the
![]() ${\varepsilon \tau }$
-calculus on the basis of a propositional logic
${\varepsilon \tau }$
-calculus on the basis of a propositional logic
![]() $\mathbf {L}$
. It is also possible to define an “extended”
$\mathbf {L}$
. It is also possible to define an “extended”
![]() ${\varepsilon \tau }$
-calculus by adding
${\varepsilon \tau }$
-calculus by adding
![]() ${\varepsilon \tau }$
-terms and critical formulas to the full first-order language including quantifiers, and then considering proofs in
${\varepsilon \tau }$
-terms and critical formulas to the full first-order language including quantifiers, and then considering proofs in
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
from critical formulas.
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
from critical formulas.
Definition 3.4. A proof
![]() $\pi $
in
$\pi $
in
![]() $(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau }$
of A is a sequence of formulas of the
$(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau }$
of A is a sequence of formulas of the
![]() ${\varepsilon \tau }$
-calculus (possibly containing quantifiers) ending in A in which each formula is either an instance of a formula in
${\varepsilon \tau }$
-calculus (possibly containing quantifiers) ending in A in which each formula is either an instance of a formula in
![]() $\mathbf {L}$
, an instance of a schema in
$\mathbf {L}$
, an instance of a schema in
![]() $\mathit {Ax}$
, a standard quantifier axiom, a critical formula, or follows from preceding formulas by modus ponens or a quantifier rule. We write
$\mathit {Ax}$
, a standard quantifier axiom, a critical formula, or follows from preceding formulas by modus ponens or a quantifier rule. We write
![]() $(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau } \vdash A$
if such a
$(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau } \vdash A$
if such a
![]() $\pi $
exists.
$\pi $
exists.
The extended
![]() ${\varepsilon \tau }$
-calculus
${\varepsilon \tau }$
-calculus
![]() $(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau }$
of
$(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau }$
of
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is the set of formulas that have proofs in
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is the set of formulas that have proofs in
![]() $(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau }$
.
$(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau }$
.
If A is quantifier-free and
![]() $\mathbf {L}{\varepsilon \tau } \vdash A$
then
$\mathbf {L}{\varepsilon \tau } \vdash A$
then
![]() $(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau } \vdash A$
. One may wonder, however, if
$(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau } \vdash A$
. One may wonder, however, if
![]() $(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau }$
is stronger than
$(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau }$
is stronger than
![]() $\mathbf {L}{\varepsilon \tau }$
in the sense that for some formulas A,
$\mathbf {L}{\varepsilon \tau }$
in the sense that for some formulas A,
![]() $(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau } \vdash A$
but not
$(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau } \vdash A$
but not
![]() $\mathbf {L}{\varepsilon \tau } \vdash A^{\varepsilon \tau }$
. This is not so as long as the
$\mathbf {L}{\varepsilon \tau } \vdash A^{\varepsilon \tau }$
. This is not so as long as the
![]() ${\varepsilon \tau }$
-translations of the axioms
${\varepsilon \tau }$
-translations of the axioms
![]() $\mathit {Ax}$
of
$\mathit {Ax}$
of
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
are provable in
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
are provable in
![]() $\mathbf {L}{\varepsilon \tau }$
; then the extended
$\mathbf {L}{\varepsilon \tau }$
; then the extended
![]() $\varepsilon $
-calculus is conservative over the pure
$\varepsilon $
-calculus is conservative over the pure
![]() $\varepsilon $
-calculus.
$\varepsilon $
-calculus.
Lemma 3.5. Suppose
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is an intermediate predicate logic, and for each quantifier axiom
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is an intermediate predicate logic, and for each quantifier axiom
![]() $B \in \mathit {Ax}$
,
$B \in \mathit {Ax}$
,
![]() $\mathbf {L}{\varepsilon \tau } \vdash B^{\varepsilon \tau }$
. If
$\mathbf {L}{\varepsilon \tau } \vdash B^{\varepsilon \tau }$
. If
![]() $(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau } \vdash A$
, then
$(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau } \vdash A$
, then
![]() $\mathbf {L}{\varepsilon \tau } \vdash A^{\varepsilon \tau }$
.
$\mathbf {L}{\varepsilon \tau } \vdash A^{\varepsilon \tau }$
.
Proof. By standard proof transformations we may assume that the proof
![]() $\pi $
in
$\pi $
in
![]() $(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau }$
is such that every formula is used as a premise of at most one modus ponens or quantifier inference, and that the eigenvariables of all quantifier inferences are distinct (the proof is regular). The proof then proceeds by induction on the length of
$(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau }$
is such that every formula is used as a premise of at most one modus ponens or quantifier inference, and that the eigenvariables of all quantifier inferences are distinct (the proof is regular). The proof then proceeds by induction on the length of
![]() $\pi $
.
$\pi $
.
Any formula B in
![]() $\pi $
that is not the conclusion of an inference is either in
$\pi $
that is not the conclusion of an inference is either in
![]() $\mathbf {L}$
, a critical formula, in
$\mathbf {L}$
, a critical formula, in
![]() $\mathit {Ax}$
, or a standard quantifier axiom. Then
$\mathit {Ax}$
, or a standard quantifier axiom. Then
![]() $B^{\varepsilon \tau }$
is also either an axiom in
$B^{\varepsilon \tau }$
is also either an axiom in
![]() $\mathbf {L}$
, a critical formula (as can easily be seen from the definition of the
$\mathbf {L}$
, a critical formula (as can easily be seen from the definition of the
![]() ${\varepsilon \tau }$
-translation), or, if
${\varepsilon \tau }$
-translation), or, if
![]() $B \in \mathit {Ax}$
then
$B \in \mathit {Ax}$
then
![]() $\mathbf {L}{\varepsilon \tau } \vdash B^{\varepsilon \tau }$
(by hypothesis). If B is a standard quantifier axiom, its
$\mathbf {L}{\varepsilon \tau } \vdash B^{\varepsilon \tau }$
(by hypothesis). If B is a standard quantifier axiom, its
![]() ${\varepsilon \tau }$
-translation is a critical formula:
${\varepsilon \tau }$
-translation is a critical formula:
 $$ \begin{align*} [A(t) \mathbin{\rightarrow} \exists x\,A(x)]^{\varepsilon\tau} &= A^{\varepsilon\tau}(t) \mathbin{\rightarrow} A^{\varepsilon\tau}(\varepsilon_{x}\,A^{\varepsilon\tau}(x)),\\ [\forall x\,A(x) \mathbin{\rightarrow} A(t)]^{\varepsilon\tau} &= A^{\varepsilon\tau}(\tau_{x}\,A^{\varepsilon\tau}(x)) \mathbin{\rightarrow} A^{\varepsilon\tau}(t). \end{align*} $$
$$ \begin{align*} [A(t) \mathbin{\rightarrow} \exists x\,A(x)]^{\varepsilon\tau} &= A^{\varepsilon\tau}(t) \mathbin{\rightarrow} A^{\varepsilon\tau}(\varepsilon_{x}\,A^{\varepsilon\tau}(x)),\\ [\forall x\,A(x) \mathbin{\rightarrow} A(t)]^{\varepsilon\tau} &= A^{\varepsilon\tau}(\tau_{x}\,A^{\varepsilon\tau}(x)) \mathbin{\rightarrow} A^{\varepsilon\tau}(t). \end{align*} $$
If
![]() $B \mathbin {\rightarrow } A(x)$
is derivable (where the eigenvariable x is not free in B), then so is
$B \mathbin {\rightarrow } A(x)$
is derivable (where the eigenvariable x is not free in B), then so is
![]() $B \mathbin {\rightarrow } A(\tau _{x}\,A(x))$
, by substituting
$B \mathbin {\rightarrow } A(\tau _{x}\,A(x))$
, by substituting
![]() $\tau _{x}\,A(x)$
everywhere x appears free in the part of
$\tau _{x}\,A(x)$
everywhere x appears free in the part of
![]() $\pi $
leading to
$\pi $
leading to
![]() $B \mathbin {\rightarrow } A(x)$
, and renaming bound variables to avoid clashes. Thus, if B is the conclusion of a quantifier inference,
$B \mathbin {\rightarrow } A(x)$
, and renaming bound variables to avoid clashes. Thus, if B is the conclusion of a quantifier inference,
![]() $\mathbf {L}{\varepsilon \tau } \vdash B^{\varepsilon \tau }$
. Similarly, if
$\mathbf {L}{\varepsilon \tau } \vdash B^{\varepsilon \tau }$
. Similarly, if
![]() $B(x) \mathbin {\rightarrow } A$
is derivable, so is
$B(x) \mathbin {\rightarrow } A$
is derivable, so is
![]() $B(\varepsilon _{x}\,B(x)) \mathbin {\rightarrow } A$
. (Cf. [Reference Moser and Zach23, Lemma 7].)⊣
$B(\varepsilon _{x}\,B(x)) \mathbin {\rightarrow } A$
. (Cf. [Reference Moser and Zach23, Lemma 7].)⊣
As we’ll see in Section 4, the quantifier axioms of the intermediate predicate logics considered in the preceding section satisfy the condition that the
![]() ${\varepsilon \tau }$
-translations of their additional quantifier axioms are derivable from critical formulas alone (i.e., already in
${\varepsilon \tau }$
-translations of their additional quantifier axioms are derivable from critical formulas alone (i.e., already in
![]() $\mathbf {L}{\varepsilon \tau }$
).
$\mathbf {L}{\varepsilon \tau }$
).
Corollary 3.6. If
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
satisfies the conditions of Lemma 3.5, and A contains no quantifiers, then
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
satisfies the conditions of Lemma 3.5, and A contains no quantifiers, then
![]() $(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau } \vdash A$
only if
$(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau } \vdash A$
only if
![]() $\mathbf {L}{\varepsilon \tau } \vdash A$
.
$\mathbf {L}{\varepsilon \tau } \vdash A$
.
Proof. If A contains no quantifiers, then
![]() $A^{\varepsilon \tau } \equiv A$
.⊣
$A^{\varepsilon \tau } \equiv A$
.⊣
Proposition 3.7. For any intermediate predicate logic
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
,
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
,
 $$ \begin{align*} & (\mathbf{Q}\mathbf{L} + \mathit{Ax}){\varepsilon\tau} \vdash \forall x\, A(x) \mathbin{\leftrightarrow} A(\tau_{x}\,A(x)) \text{ and}\\ &(\mathbf{Q}\mathbf{L}+\mathit{Ax}){\varepsilon\tau} \vdash \exists x\, A(x) \mathbin{\leftrightarrow} A(\varepsilon_{x}\,A(x)). \end{align*} $$
$$ \begin{align*} & (\mathbf{Q}\mathbf{L} + \mathit{Ax}){\varepsilon\tau} \vdash \forall x\, A(x) \mathbin{\leftrightarrow} A(\tau_{x}\,A(x)) \text{ and}\\ &(\mathbf{Q}\mathbf{L}+\mathit{Ax}){\varepsilon\tau} \vdash \exists x\, A(x) \mathbin{\leftrightarrow} A(\varepsilon_{x}\,A(x)). \end{align*} $$
Proof. In each case, one direction is an instance of the corresponding quantifier axiom, and the other direction follows from a critical formula by the corresponding quantifier rule. For instance,
![]() $A(\varepsilon _{x}\,A(x)) \mathbin {\rightarrow } \exists x\, A(x)$
is a standard quantifier axiom, and from the critical formula
$A(\varepsilon _{x}\,A(x)) \mathbin {\rightarrow } \exists x\, A(x)$
is a standard quantifier axiom, and from the critical formula
![]() $A(x) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x))$
we get
$A(x) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x))$
we get
![]() $\exists x\, A(x) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x))$
by the
$\exists x\, A(x) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x))$
by the
![]() $\exists $
-rule, since x is not free in
$\exists $
-rule, since x is not free in
![]() $A(\varepsilon _{x}\,A(x))$
.⊣
$A(\varepsilon _{x}\,A(x))$
.⊣
Proposition 3.8. If
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}$
satisfies the conditions of Lemma 3.5, then
$\mathbf {Q}\mathbf {L}+\mathit {Ax}$
satisfies the conditions of Lemma 3.5, then
![]() $(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau } \vdash A \mathbin {\leftrightarrow } A^{\varepsilon \tau }$
.
$(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau } \vdash A \mathbin {\leftrightarrow } A^{\varepsilon \tau }$
.
Proof. Since
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}$
includes
$\mathbf {Q}\mathbf {L}+\mathit {Ax}$
includes
![]() $\mathbf {Q}\mathbf {H}$
, the substitution rule
$\mathbf {Q}\mathbf {H}$
, the substitution rule
![]() $B \mathbin {\leftrightarrow } C \vdash D(B) \mathbin {\leftrightarrow } D(C)$
is admissible. The result follows by induction on complexity of A and the previous proposition.⊣
$B \mathbin {\leftrightarrow } C \vdash D(B) \mathbin {\leftrightarrow } D(C)$
is admissible. The result follows by induction on complexity of A and the previous proposition.⊣
4 Critical formulas and quantifier shifts
We will show later (Theorem 5.3) that any
![]() ${\varepsilon \tau }$
-calculus for an intermediate logic
${\varepsilon \tau }$
-calculus for an intermediate logic
![]() $\mathbf {L}$
is conservative over
$\mathbf {L}$
is conservative over
![]() $\mathbf {L}$
. It is well-known that the
$\mathbf {L}$
. It is well-known that the
![]() ${\varepsilon \tau }$
-calculus over intuitionistic logic is not conservative over intuitionistic predicate logic. We’ll show now specifically that for any intermediate logic
${\varepsilon \tau }$
-calculus over intuitionistic logic is not conservative over intuitionistic predicate logic. We’ll show now specifically that for any intermediate logic
![]() $\mathbf {L}$
, the
$\mathbf {L}$
, the
![]() ${\varepsilon \tau }$
-translations of all classically valid quantifier shift principles are provable from critical formulas.
${\varepsilon \tau }$
-translations of all classically valid quantifier shift principles are provable from critical formulas.
Quantifier shift formulas divide into two kinds. On the one hand, we have conditionals the
![]() ${\varepsilon \tau }$
-translations of which are critical formulas, and are therefore provable in
${\varepsilon \tau }$
-translations of which are critical formulas, and are therefore provable in
![]() $\mathbf {L}{\varepsilon \tau }$
(see Table 3). On the other hand, we have formulas provable from critical formulas together with some propositional principles, all of which are intuitionistically valid and hence provable in all intermediate logics. For instance, to obtain the
$\mathbf {L}{\varepsilon \tau }$
(see Table 3). On the other hand, we have formulas provable from critical formulas together with some propositional principles, all of which are intuitionistically valid and hence provable in all intermediate logics. For instance, to obtain the
![]() ${\varepsilon \tau }$
-translation of
${\varepsilon \tau }$
-translation of
take
![]() $A_{1} = A(\tau _{x}\,A(x))$
and
$A_{1} = A(\tau _{x}\,A(x))$
and
![]() $A_{2} = A(\tau _{x}\,(A(x) \lor B))$
. Then
$A_{2} = A(\tau _{x}\,(A(x) \lor B))$
. Then
![]() $A_{1} \mathbin {\rightarrow } A_{2}$
is a critical formula, viz.,
$A_{1} \mathbin {\rightarrow } A_{2}$
is a critical formula, viz.,
Apply modus ponens to it and the principle
This same pattern works in all cases, and the required critical formulas
![]() $A_{1} \mathbin {\rightarrow } A_{2}$
and propositional principles are given in Table 4.
$A_{1} \mathbin {\rightarrow } A_{2}$
and propositional principles are given in Table 4.
Table 3 Quantifier shift formulas whose
![]() ${\varepsilon \tau }$
-translations are critical formulas. In each case, x is not free in B, and the
${\varepsilon \tau }$
-translations are critical formulas. In each case, x is not free in B, and the
![]() ${\varepsilon \tau }$
-translation of the quantifier shift formula on the left is
${\varepsilon \tau }$
-translation of the quantifier shift formula on the left is
![]() $C(t_{1}) \mathbin {\rightarrow } C(t_{2})$
.
$C(t_{1}) \mathbin {\rightarrow } C(t_{2})$
.

Table 4 Proofs of
![]() ${\varepsilon \tau }$
-translations of quantifier shift formulas. In each case, x is not free in B,
${\varepsilon \tau }$
-translations of quantifier shift formulas. In each case, x is not free in B,
![]() $A_{1} \mathbin {\rightarrow } A_{2}$
is a critical formula, and the
$A_{1} \mathbin {\rightarrow } A_{2}$
is a critical formula, and the
![]() ${\varepsilon \tau }$
-translation of the formula is given on the left. The propositional principle on the right is provable in intuitionistic logic, and the
${\varepsilon \tau }$
-translation of the formula is given on the left. The propositional principle on the right is provable in intuitionistic logic, and the
![]() ${\varepsilon \tau }$
-translation of the quantifier shift formula follows by one application of modus ponens.
${\varepsilon \tau }$
-translation of the quantifier shift formula follows by one application of modus ponens.

The most interesting quantifier shift formulas here are
![]() $\mathit {CD}$
,
$\mathit {CD}$
,
![]() $Q_{\forall }$
, and
$Q_{\forall }$
, and
![]() $Q_{\exists }$
, since they are not intuitionistically valid. By contrast, we have:
$Q_{\exists }$
, since they are not intuitionistically valid. By contrast, we have:
Proposition 4.1. If
![]() $\mathbf {L}$
is an intermediate propositional logic, then
$\mathbf {L}$
is an intermediate propositional logic, then
![]() $:$
$:$
-
1.
 $K^{\varepsilon \tau }$
,
$K^{\varepsilon \tau }$
,
 $\mathit {CD}^{\varepsilon \tau }$
,
$\mathit {CD}^{\varepsilon \tau }$
,
 $(Q_{\exists })^{\varepsilon \tau }$
, and
$(Q_{\exists })^{\varepsilon \tau }$
, and
 $(Q_{\forall })^{\varepsilon \tau }$
are provable in
$(Q_{\forall })^{\varepsilon \tau }$
are provable in
 $\mathbf {L}{\varepsilon \tau }$
.
$\mathbf {L}{\varepsilon \tau }$
. -
2. K,
 $\mathit {CD}$
,
$\mathit {CD}$
,
 $Q_{\exists }$
, and
$Q_{\exists }$
, and
 $Q_{\forall }$
are provable in
$Q_{\forall }$
are provable in
 $(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau }$
.
$(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau }$
.
The second
![]() $\varepsilon $
-theorem states that if
$\varepsilon $
-theorem states that if
![]() $A^{\varepsilon }$
is provable in the pure
$A^{\varepsilon }$
is provable in the pure
![]() $\varepsilon $
-calculus, then A is provable in classical predicate logic. The second
$\varepsilon $
-calculus, then A is provable in classical predicate logic. The second
![]() $\varepsilon $
-theorem fails for any intermediate predicate logic
$\varepsilon $
-theorem fails for any intermediate predicate logic
![]() $\mathbf {Q}\mathbf {L} +\mathit {Ax}$
, in which
$\mathbf {Q}\mathbf {L} +\mathit {Ax}$
, in which
![]() $A^{\varepsilon \tau }$
is provable in
$A^{\varepsilon \tau }$
is provable in
![]() $\mathbf {L}{\varepsilon \tau }$
but A is not provable in
$\mathbf {L}{\varepsilon \tau }$
but A is not provable in
![]() $\mathbf {Q}\mathbf {L} +\mathit {Ax}$
, e.g., when
$\mathbf {Q}\mathbf {L} +\mathit {Ax}$
, e.g., when
![]() $\mathbf {Q}\mathbf {L} +\mathit {Ax}$
does not prove one of K,
$\mathbf {Q}\mathbf {L} +\mathit {Ax}$
does not prove one of K,
![]() $\mathit {CD}$
,
$\mathit {CD}$
,
![]() $Q_{\exists }$
, or
$Q_{\exists }$
, or
![]() $Q_{\forall }$
.
$Q_{\forall }$
.
Note that the only intuitionistically invalid De Morgan rule for quantifiers,
is a special case of
![]() $Q_{\forall }$
, taking
$Q_{\forall }$
, taking
![]() $\bot $
for B;
$\bot $
for B;
![]() $Q^{\varepsilon \tau }$
is a critical formula. The
$Q^{\varepsilon \tau }$
is a critical formula. The
![]() ${\varepsilon \tau }$
-translation of double negation shift
${\varepsilon \tau }$
-translation of double negation shift
![]() $K^{\varepsilon \tau }$
is
$K^{\varepsilon \tau }$
is
and is also a critical formula.
In classical first-order logic, both the addition of
![]() $\varepsilon $
-operators and critical formulas and the replacement of quantifiers by
$\varepsilon $
-operators and critical formulas and the replacement of quantifiers by
![]() $\varepsilon $
-operators are conservative. The previous results show that for extensions of first-order intuitionistic logic, this is not the case: intuitionistically invalid quantified formulas (or their
$\varepsilon $
-operators are conservative. The previous results show that for extensions of first-order intuitionistic logic, this is not the case: intuitionistically invalid quantified formulas (or their
![]() ${\varepsilon \tau }$
-translations) become provable. However, these quantifier shifts are provable in some intermediate logics, e.g., in some Gödel logics.
${\varepsilon \tau }$
-translations) become provable. However, these quantifier shifts are provable in some intermediate logics, e.g., in some Gödel logics.
We might think of
![]() ${\varepsilon \tau }$
-terms semantically as terms for objects which serve the role of generics taking on the role of quantifiers, and indeed in classical logic this connection is very close. Because of the validity of
${\varepsilon \tau }$
-terms semantically as terms for objects which serve the role of generics taking on the role of quantifiers, and indeed in classical logic this connection is very close. Because of the validity of
in classical logic, there always is an object x which behaves as an
![]() $\varepsilon $
-term (
$\varepsilon $
-term (
![]() $A(x)$
holds iff
$A(x)$
holds iff
![]() $\exists x\,A(x)$
holds), and an object x which behaves as a
$\exists x\,A(x)$
holds), and an object x which behaves as a
![]() $\tau $
-term (i.e.,
$\tau $
-term (i.e.,
![]() $A(x)$
holds iff
$A(x)$
holds iff
![]() $\forall y\,A(y)$
holds). One might expect then that
$\forall y\,A(y)$
holds). One might expect then that
![]() $\mathit {Wel}_{1}$
and
$\mathit {Wel}_{1}$
and
![]() $\mathit {Wel}_{2}$
, when added to
$\mathit {Wel}_{2}$
, when added to
![]() $\mathbf {Q}\mathbf {H}$
, have the same effect as adding critical formulas, i.e., that all quantifier shifts become provable. Note that
$\mathbf {Q}\mathbf {H}$
, have the same effect as adding critical formulas, i.e., that all quantifier shifts become provable. Note that
![]() $\mathit {Wel}_{1}$
and
$\mathit {Wel}_{1}$
and
![]() $\mathit {Wel}_{2}$
are intuitionistically equivalent to
$\mathit {Wel}_{2}$
are intuitionistically equivalent to
As is easily checked,
![]() $\mathbf {Q}\mathbf {H} \vdash \mathit {Wel}_{1} \mathbin {\leftrightarrow } Q_{\exists }$
and
$\mathbf {Q}\mathbf {H} \vdash \mathit {Wel}_{1} \mathbin {\leftrightarrow } Q_{\exists }$
and
![]() $\mathbf {Q}\mathbf {H} \vdash \mathit {Wel}_{2} \mathbin {\leftrightarrow } Q_{\forall }$
, and even
$\mathbf {Q}\mathbf {H} \vdash \mathit {Wel}_{2} \mathbin {\leftrightarrow } Q_{\forall }$
, and even
![]() $\mathbf {Q}\mathbf {H} \vdash \mathit {Wel}_{2} \mathbin {\rightarrow } \mathit {CD}$
. However,
$\mathbf {Q}\mathbf {H} \vdash \mathit {Wel}_{2} \mathbin {\rightarrow } \mathit {CD}$
. However,
![]() $\mathbf {Q}\mathbf {H} + \mathit {Wel}_{1} \nvdash \mathit {CD}$
.Footnote
4
$\mathbf {Q}\mathbf {H} + \mathit {Wel}_{1} \nvdash \mathit {CD}$
.Footnote
4
5
 $\mathbf {L}{\varepsilon \tau }$
is conservative over
$\mathbf {L}{\varepsilon \tau }$
is conservative over
 $\mathbf {L}$
$\mathbf {L}$
The classical
![]() $\varepsilon $
-calculus is conservative over propositional logic. Work by Bell [Reference Bell9] and DeVidi [Reference DeVidi12] shows that, however, the addition of critical formulas to intuitionistic logic results in intuitionistically invalid propositional formulas becoming provable in certain simple theories. These results require the presence of identity axioms. One may wonder if these results can be strengthened to the pure logic and the
$\varepsilon $
-calculus is conservative over propositional logic. Work by Bell [Reference Bell9] and DeVidi [Reference DeVidi12] shows that, however, the addition of critical formulas to intuitionistic logic results in intuitionistically invalid propositional formulas becoming provable in certain simple theories. These results require the presence of identity axioms. One may wonder if these results can be strengthened to the pure logic and the
![]() ${\varepsilon \tau }$
-calculus alone. The following proposition shows that this is not the case. The addition of critical formulas to intermediate logics alone does not have any effects on the propositional level.
${\varepsilon \tau }$
-calculus alone. The following proposition shows that this is not the case. The addition of critical formulas to intermediate logics alone does not have any effects on the propositional level.
Definition 5.1. The shadow
![]() $A^{s}$
of a formula is defined as follows:
$A^{s}$
of a formula is defined as follows:
 $$ \begin{align*} P(t_{1}, \ldots, t_{n})^{s} & = X_{P},\\ (t_{1} = t_{2})^{s} & = \top,\\ (A \land B)^{s} & = A^{s} \land B^{s}, & (A \lor B)^{s} & = A^{s} \lor B^{s}, \\ (A \mathbin{\rightarrow} B)^{s} & = A^{s} \mathbin{\rightarrow} B^{s}, & (\lnot A)^{s} & = \lnot A^{s}, \\ (\exists x\, A(x))^{s} & = A(x)^{s}, & (\forall x\, A(x))^{s} & = A(x)^{s}, \end{align*} $$
$$ \begin{align*} P(t_{1}, \ldots, t_{n})^{s} & = X_{P},\\ (t_{1} = t_{2})^{s} & = \top,\\ (A \land B)^{s} & = A^{s} \land B^{s}, & (A \lor B)^{s} & = A^{s} \lor B^{s}, \\ (A \mathbin{\rightarrow} B)^{s} & = A^{s} \mathbin{\rightarrow} B^{s}, & (\lnot A)^{s} & = \lnot A^{s}, \\ (\exists x\, A(x))^{s} & = A(x)^{s}, & (\forall x\, A(x))^{s} & = A(x)^{s}, \end{align*} $$
where
![]() $X_{P}$
is a propositional variable and
$X_{P}$
is a propositional variable and
![]() $\top $
is any theorem of
$\top $
is any theorem of
![]() $\mathbf {L}$
.
$\mathbf {L}$
.
The shadow of a proof
![]() $\pi = A_{1}$
, …,
$\pi = A_{1}$
, …,
![]() $A_{n}$
is
$A_{n}$
is
![]() $A_{1}^{s}$
, …,
$A_{1}^{s}$
, …,
![]() $A_{n}^{s}$
.
$A_{n}^{s}$
.
A first-order intermediate logic
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
(over a propositional base logic
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
(over a propositional base logic
![]() $\mathbf {L}$
) is preserved under shadow if
$\mathbf {L}$
) is preserved under shadow if
![]() $\mathbf {L} \vdash B^{s}$
for all quantifier axioms
$\mathbf {L} \vdash B^{s}$
for all quantifier axioms
![]() $B \in \mathit {Ax}$
.
$B \in \mathit {Ax}$
.
The shadow of a formula is a propositional formula obtained by disregarding all first-order structure. If an intermediate predicate logic
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is preserved under shadow, the shadows of its theorems are already valid in
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is preserved under shadow, the shadows of its theorems are already valid in
![]() $\mathbf {L}$
.
$\mathbf {L}$
.
Proposition 5.2. Suppose
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}$
is preserved under shadow. If
$\mathbf {Q}\mathbf {L}+\mathit {Ax}$
is preserved under shadow. If
![]() $A_{1}, \ldots , A_{n} \vdash _{(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau }} B$
, then
$A_{1}, \ldots , A_{n} \vdash _{(\mathbf {Q}\mathbf {L} + \mathit {Ax}){\varepsilon \tau }} B$
, then
![]() $A_{1}^{s}, \ldots , A_{n}^{s} \vdash _{\mathbf {L}} B^{s}$
. This also holds if identity axioms are present.
$A_{1}^{s}, \ldots , A_{n}^{s} \vdash _{\mathbf {L}} B^{s}$
. This also holds if identity axioms are present.
Proof. Consider a derivation
![]() $\pi $
in
$\pi $
in
![]() $(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau }$
of B from
$(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau }$
of B from
![]() $A_{1}$
, …,
$A_{1}$
, …,
![]() $A_{n}$
, and a formula C in
$A_{n}$
, and a formula C in
![]() $\pi $
not a conclusion of an inference, and not among
$\pi $
not a conclusion of an inference, and not among
![]() $A_{1}$
, …,
$A_{1}$
, …,
![]() $A_{n}$
. If
$A_{n}$
. If
![]() $C \in \mathbf {L}$
, then also
$C \in \mathbf {L}$
, then also
![]() $C^{s} \in \mathbf {L}$
. If C is a critical formula, then
$C^{s} \in \mathbf {L}$
. If C is a critical formula, then
![]() $C^{s}$
is of the form
$C^{s}$
is of the form
![]() $A \mathbin {\rightarrow } A$
. If C is a standard quantifier axiom, we have
$A \mathbin {\rightarrow } A$
. If C is a standard quantifier axiom, we have
![]() $(\forall x\, A \mathbin {\rightarrow } A(t))^{s} \equiv (A(t) \mathbin {\rightarrow } \exists x\, A(x))^{s} \equiv A(x)^{s} \mathbin {\rightarrow } A(x)^{s}$
, which again is in
$(\forall x\, A \mathbin {\rightarrow } A(t))^{s} \equiv (A(t) \mathbin {\rightarrow } \exists x\, A(x))^{s} \equiv A(x)^{s} \mathbin {\rightarrow } A(x)^{s}$
, which again is in
![]() $\mathbf {L}$
. (Clearly,
$\mathbf {L}$
. (Clearly,
![]() $A(t)^{s} \equiv A(x)^{s}$
.)
$A(t)^{s} \equiv A(x)^{s}$
.)
If C is the conclusion of modus ponens from premises A and
![]() $A \mathbin {\rightarrow } C$
, then
$A \mathbin {\rightarrow } C$
, then
![]() $C^{s}$
follows from
$C^{s}$
follows from
![]() $A^{s}$
and
$A^{s}$
and
![]() $(A \mathbin {\rightarrow } C)^{s}$
by modus ponens. If C is the conclusion of a quantifier rule, the shadows of premise and conclusion are identical, e.g.,
$(A \mathbin {\rightarrow } C)^{s}$
by modus ponens. If C is the conclusion of a quantifier rule, the shadows of premise and conclusion are identical, e.g.,
Thus we have shown that
![]() $\pi ^{s}$
is a derivation of
$\pi ^{s}$
is a derivation of
![]() $B^{s}$
from
$B^{s}$
from
![]() $A_{1}^{s}$
, …,
$A_{1}^{s}$
, …,
![]() $A_{n}^{s}$
in
$A_{n}^{s}$
in
![]() $\mathbf {L}$
.
$\mathbf {L}$
.
This still holds if identity is present, as the shadows of identity axioms are:
![]() $(t = t)^{s} \equiv \top $
and
$(t = t)^{s} \equiv \top $
and
since
![]() $A(t_{1})^{s} \equiv A(t_{2})^{s}$
. Both are provable in
$A(t_{1})^{s} \equiv A(t_{2})^{s}$
. Both are provable in
![]() $\mathbf {H}{}$
and thus in
$\mathbf {H}{}$
and thus in
![]() $\mathbf {L}$
.⊣
$\mathbf {L}$
.⊣
All intermediate predicate logics mentioned above are preserved under shadow. They are axiomatized by various quantifier shift principles. As we have seen in the preceding section, the
![]() ${\varepsilon \tau }$
-translations of all such quantifier shift principles become provable in the corresponding
${\varepsilon \tau }$
-translations of all such quantifier shift principles become provable in the corresponding
![]() ${\varepsilon \tau }$
-calculus. However, the shadow of such a quantifier shift principle is a formula of the form
${\varepsilon \tau }$
-calculus. However, the shadow of such a quantifier shift principle is a formula of the form
![]() $B \mathbin {\rightarrow } B$
. As a consequence, we have the following conservativity result for all intermediate
$B \mathbin {\rightarrow } B$
. As a consequence, we have the following conservativity result for all intermediate
![]() ${\varepsilon \tau }$
-calculi:
${\varepsilon \tau }$
-calculi:
Theorem 5.3. If
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is preserved under shadow, then
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
is preserved under shadow, then
![]() $(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau }$
is conservative over
$(\mathbf {Q}\mathbf {L}+\mathit {Ax}){\varepsilon \tau }$
is conservative over
![]() $\mathbf {L}$
for propositional formulas. In particular, no new propositional formulas become provable in
$\mathbf {L}$
for propositional formulas. In particular, no new propositional formulas become provable in
![]() $\mathbf {L}{\varepsilon \tau }$
by the addition of critical formulas to any intermediate logic
$\mathbf {L}{\varepsilon \tau }$
by the addition of critical formulas to any intermediate logic
![]() $\mathbf {L}$
, including intuitionistic logic itself.
$\mathbf {L}$
, including intuitionistic logic itself.
Bell [Reference Bell9] claimed that in the extended intuitionistic
![]() $\varepsilon $
-calculus for
$\varepsilon $
-calculus for
![]() $\mathbf {Q}\mathbf {H}$
with identity, we have
$\mathbf {Q}\mathbf {H}$
with identity, we have
![]() $D \vdash _{\mathbf {Q}\mathbf {H}{\varepsilon \tau }} M$
, where M is
$D \vdash _{\mathbf {Q}\mathbf {H}{\varepsilon \tau }} M$
, where M is
and D is
![]() $\forall x(x = a \lor \lnot x =a)$
. M is an intuitionistically invalid direction of De Morgan’s laws. Since the shadow
$\forall x(x = a \lor \lnot x =a)$
. M is an intuitionistically invalid direction of De Morgan’s laws. Since the shadow
![]() $D^{s}$
of D is the intuitionistically valid formula
$D^{s}$
of D is the intuitionistically valid formula
![]() $\top \lor \lnot \top $
, this seems to contradict Lemma 5.2. The proof starts by asserting that
$\top \lor \lnot \top $
, this seems to contradict Lemma 5.2. The proof starts by asserting that
is provable in
![]() $\mathbf {Q}\mathbf {H}$
with identity. This is false, however, as the formula is not true in any one-element model when B is true and C is false. Theorem 7 of [Reference DeVidi12] fails for the same reason. The results are correct with the additional assumption
$\mathbf {Q}\mathbf {H}$
with identity. This is false, however, as the formula is not true in any one-element model when B is true and C is false. Theorem 7 of [Reference DeVidi12] fails for the same reason. The results are correct with the additional assumption
![]() $a \neq b$
.Footnote
5
$a \neq b$
.Footnote
5
6 The extended first
 ${\varepsilon \tau }$
-theorem fails unless
${\varepsilon \tau }$
-theorem fails unless
 $\mathbf {L} \vdash B_{m}$
$\mathbf {L} \vdash B_{m}$
In classical first-order logic, the main result about the
![]() $\varepsilon $
-calculus is the extended first
$\varepsilon $
-calculus is the extended first
![]() $\varepsilon $
-theorem. It states that if
$\varepsilon $
-theorem. It states that if
![]() $A(e_{1}, \dots , e_{n})$
, where the
$A(e_{1}, \dots , e_{n})$
, where the
![]() $e_{i}$
are
$e_{i}$
are
![]() $\varepsilon $
-terms, is provable in the pure
$\varepsilon $
-terms, is provable in the pure
![]() $\varepsilon $
-calculus, then there are
$\varepsilon $
-calculus, then there are
![]() $\varepsilon $
-free terms
$\varepsilon $
-free terms
![]() $t_{i}^{j}$
such that
$t_{i}^{j}$
such that
is provable in classical propositional logic alone. Such
![]() $\varepsilon $
-terms
$\varepsilon $
-terms
![]() $e_{i}$
appear as the result of translating
$e_{i}$
appear as the result of translating
![]() $\exists x_{1}\dots \exists x_{n}\,A(x_{1}, \dots , x_{n})$
into the
$\exists x_{1}\dots \exists x_{n}\,A(x_{1}, \dots , x_{n})$
into the
![]() $\varepsilon $
-calculus.
$\varepsilon $
-calculus.
In the context of intermediate logics, we may formulate the statement as follows:
Definition 6.1. An intermediate logic
![]() $\mathbf {L}$
has the extended first
$\mathbf {L}$
has the extended first
![]() ${\varepsilon \tau }$
-theorem, if, whenever
${\varepsilon \tau }$
-theorem, if, whenever
![]() $\mathbf {L}{\varepsilon \tau } \vdash A(e_{1}, \dots , e_{n})$
for some
$\mathbf {L}{\varepsilon \tau } \vdash A(e_{1}, \dots , e_{n})$
for some
![]() $\varepsilon $
- or
$\varepsilon $
- or
![]() $\tau $
-terms
$\tau $
-terms
![]() $e_{1}$
, …,
$e_{1}$
, …,
![]() $e_{n}$
, then there are
$e_{n}$
, then there are
![]() ${\varepsilon \tau }$
-free terms
${\varepsilon \tau }$
-free terms
![]() $t_{i}^{j}$
such that
$t_{i}^{j}$
such that
We obtain a first negative result: if
![]() $\mathbf {L}{\varepsilon \tau }$
has the extended first epsilon theorem, then an instance of
$\mathbf {L}{\varepsilon \tau }$
has the extended first epsilon theorem, then an instance of
![]() ${B_{m}}$
, i.e.,
${B_{m}}$
, i.e.,
for some
![]() $m \ge 2$
is provable already in the propositional fragment
$m \ge 2$
is provable already in the propositional fragment
![]() $\mathbf {L}$
.Footnote
6
This rules out an extended first
$\mathbf {L}$
.Footnote
6
This rules out an extended first
![]() ${\varepsilon \tau }$
-theorem for, e.g.,
${\varepsilon \tau }$
-theorem for, e.g.,
![]() ${\varepsilon \tau }$
-calculi for intuitionistic logic and infinite-valued Gödel–Dummett logic.
${\varepsilon \tau }$
-calculi for intuitionistic logic and infinite-valued Gödel–Dummett logic.
Theorem 6.2. Suppose
![]() $\mathbf {L}{\varepsilon \tau }$
has the extended first
$\mathbf {L}{\varepsilon \tau }$
has the extended first
![]() ${\varepsilon \tau }$
-theorem. Then
${\varepsilon \tau }$
-theorem. Then
![]() $\mathbf {L} \vdash {B_{m}}$
for some
$\mathbf {L} \vdash {B_{m}}$
for some
![]() $m \ge 2$
.
$m \ge 2$
.
Proof. Consider
![]() $A(z) \equiv (P(f(z)) \mathbin {\rightarrow } P(z))$
and
$A(z) \equiv (P(f(z)) \mathbin {\rightarrow } P(z))$
and
![]() $\exists z\, A(z)$
, i.e.,
$\exists z\, A(z)$
, i.e.,
![]() $\exists z(P(f(z)) \mathbin {\rightarrow } P(z))$
. Let
$\exists z(P(f(z)) \mathbin {\rightarrow } P(z))$
. Let
![]() $e \equiv \varepsilon _{z}\,(P(f(z)) \mathbin {\rightarrow } P(z))$
. The
$e \equiv \varepsilon _{z}\,(P(f(z)) \mathbin {\rightarrow } P(z))$
. The
![]() ${\varepsilon \tau }$
-translation of
${\varepsilon \tau }$
-translation of
![]() $\exists z\, A(z)$
is
$\exists z\, A(z)$
is
![]() $P(f(e)) \mathbin {\rightarrow } P(e)$
, i.e.,
$P(f(e)) \mathbin {\rightarrow } P(e)$
, i.e.,
Let
![]() $U \equiv A(\varepsilon _{x}\,P(x)) \equiv P(f(\varepsilon _{x}\,P(x))) \mathbin {\rightarrow } P(\varepsilon _{x}\,P(x))$
. Note that U is of the form
$U \equiv A(\varepsilon _{x}\,P(x)) \equiv P(f(\varepsilon _{x}\,P(x))) \mathbin {\rightarrow } P(\varepsilon _{x}\,P(x))$
. Note that U is of the form
![]() $P(t) \mathbin {\rightarrow } P(\varepsilon _{x}\,P(x))$
, so it is a critical formula. Also note that
$P(t) \mathbin {\rightarrow } P(\varepsilon _{x}\,P(x))$
, so it is a critical formula. Also note that
![]() $U \mathbin {\rightarrow } V$
is of the form
$U \mathbin {\rightarrow } V$
is of the form
![]() $A(t) \mathbin {\rightarrow } A(e)$
, and so
$A(t) \mathbin {\rightarrow } A(e)$
, and so
![]() $U \mathbin {\rightarrow } V$
is also a critical formula.
$U \mathbin {\rightarrow } V$
is also a critical formula.
Since
![]() $\mathbf {L} \vdash (U \mathbin {\rightarrow } V) \mathbin {\rightarrow } (U \mathbin {\rightarrow } V)$
, and
$\mathbf {L} \vdash (U \mathbin {\rightarrow } V) \mathbin {\rightarrow } (U \mathbin {\rightarrow } V)$
, and
![]() $U \mathbin {\rightarrow } V$
and U are critical formulas,
$U \mathbin {\rightarrow } V$
and U are critical formulas,
![]() $\mathbf {L}{\varepsilon \tau } \vdash V$
. By assumption,
$\mathbf {L}{\varepsilon \tau } \vdash V$
. By assumption,
![]() $\mathbf {L}{\varepsilon \tau }$
has the extended first
$\mathbf {L}{\varepsilon \tau }$
has the extended first
![]() ${\varepsilon \tau }$
-theorem, so
${\varepsilon \tau }$
-theorem, so
![]() $\mathbf {L}$
proves a disjunction of the form
$\mathbf {L}$
proves a disjunction of the form
for some terms
![]() $t_{1}$
, …,
$t_{1}$
, …,
![]() $t_{k}$
. (This is a Herbrand disjunction of
$t_{k}$
. (This is a Herbrand disjunction of
![]() $\exists z\, A(z)$
.) Each term
$\exists z\, A(z)$
.) Each term
![]() $t_{i}$
is of the form
$t_{i}$
is of the form
![]() $f^{i}(s)$
for some
$f^{i}(s)$
for some
![]() $i \ge 0$
and a term s which does not start with f. By rearranging the disjuncts to group disjuncts with the same innermost term s together (using commutativity of
$i \ge 0$
and a term s which does not start with f. By rearranging the disjuncts to group disjuncts with the same innermost term s together (using commutativity of
![]() $\lor $
) and by adding additional disjuncts as needed (using weakening), from this we obtain a formula
$\lor $
) and by adding additional disjuncts as needed (using weakening), from this we obtain a formula
 $$ \begin{align*} (P(f^{j_{1}+1}(s_{1})) \mathbin{\rightarrow} P(f^{j_{1}}(s_{1}))) \lor {} & \dots \lor (P(f(s_{1})) \mathbin{\rightarrow} P(s_{1})) \lor \\ & \vdots \\ (P(f^{j_{l}+1}(s_{l})) \mathbin{\rightarrow} P(f^{j_{l}}(s_{l}))) \lor {} & \dots \lor (P(f(s_{l})) \mathbin{\rightarrow} P(s_{l})). \end{align*} $$
$$ \begin{align*} (P(f^{j_{1}+1}(s_{1})) \mathbin{\rightarrow} P(f^{j_{1}}(s_{1}))) \lor {} & \dots \lor (P(f(s_{1})) \mathbin{\rightarrow} P(s_{1})) \lor \\ & \vdots \\ (P(f^{j_{l}+1}(s_{l})) \mathbin{\rightarrow} P(f^{j_{l}}(s_{l}))) \lor {} & \dots \lor (P(f(s_{l})) \mathbin{\rightarrow} P(s_{l})). \end{align*} $$
Let j be the largest among
![]() $j_{1}$
, …,
$j_{1}$
, …,
![]() $j_{l}$
. By uniformly replacing
$j_{l}$
. By uniformly replacing
![]() $P(f^{i}(s_{j}))$
by
$P(f^{i}(s_{j}))$
by
![]() $A_{j+2-i}$
in the proof of the last formula and contracting identical disjuncts, we obtain a proof in
$A_{j+2-i}$
in the proof of the last formula and contracting identical disjuncts, we obtain a proof in
![]() $\mathbf {L}$
of
$\mathbf {L}$
of
![]() $(A_{1} \mathbin {\rightarrow } A_{2}) \lor \dots \lor (A_{j+1} \mathbin {\rightarrow } A_{j+2})$
. This is
$(A_{1} \mathbin {\rightarrow } A_{2}) \lor \dots \lor (A_{j+1} \mathbin {\rightarrow } A_{j+2})$
. This is
![]() ${B_{m}}$
for
${B_{m}}$
for
![]() $m=j+1$
, and since
$m=j+1$
, and since
![]() $j\ge 1$
,
$j\ge 1$
,
![]() $m\ge 2$
.⊣
$m\ge 2$
.⊣
A formula of the form
![]() ${B_{m}}$
is provable in
${B_{m}}$
is provable in
![]() $\mathbf {L}$
iff
$\mathbf {L}$
iff
![]() $\mathbf {L}$
is a finite-valued Gödel logic
$\mathbf {L}$
is a finite-valued Gödel logic
![]() $\mathbf {LC}_{n}$
(Proposition 6.5). By contrast, no
$\mathbf {LC}_{n}$
(Proposition 6.5). By contrast, no
![]() ${B_{m}}$
is provable in intuitionistic logic
${B_{m}}$
is provable in intuitionistic logic
![]() $\mathbf {H}$
, Jankov logic
$\mathbf {H}$
, Jankov logic
![]() $\mathbf {KC}$
, or infinite-valued Gödel logic
$\mathbf {KC}$
, or infinite-valued Gödel logic
![]() $\mathbf {LC}$
(Proposition 6.3).
$\mathbf {LC}$
(Proposition 6.3).
Proposition 6.3.
-
1.
 $\mathbf {LC}_{m} \vdash {B_{m}}$
.
$\mathbf {LC}_{m} \vdash {B_{m}}$
. -
2.
 $\mathbf {L} \not \vdash {B_{n}}$
for
$\mathbf {L} \not \vdash {B_{n}}$
for
 $\mathbf {L}$
any of
$\mathbf {L}$
any of
 $\mathbf {LC}_{m}$
with
$\mathbf {LC}_{m}$
with
 $m>n$
,
$m>n$
,
 $\mathbf {LC}$
,
$\mathbf {LC}$
,
 $\mathbf {KC}$
, or
$\mathbf {KC}$
, or
 $\mathbf {H}$
.
$\mathbf {H}$
.
Proof. (1) Follows by definition, since
![]() $\mathbf {LC}_{m} = \mathbf {LC} + {B_{m}}$
.
$\mathbf {LC}_{m} = \mathbf {LC} + {B_{m}}$
.
(2) Let
![]() $v(A_{i}) = 1/i$
if
$v(A_{i}) = 1/i$
if
![]() $i < n$
and
$i < n$
and
![]() $v(A_{n+1}) = 0$
. This is a valuation in a truth value set with m elements if
$v(A_{n+1}) = 0$
. This is a valuation in a truth value set with m elements if
![]() $m> n$
(i.e., a valuation in the Gödel semantics for
$m> n$
(i.e., a valuation in the Gödel semantics for
![]() $\mathbf {LC}_{m}$
). It is also a valuation in the infinite truth value set
$\mathbf {LC}_{m}$
). It is also a valuation in the infinite truth value set
![]() $[0,1]$
of
$[0,1]$
of
![]() $\mathbf {LC}$
. For all
$\mathbf {LC}$
. For all
![]() $i \le n$
,
$i \le n$
,
![]() $v(A_{i})> v(A_{i+1})$
and hence
$v(A_{i})> v(A_{i+1})$
and hence
![]() $v({B_{n}}) < 1$
. So
$v({B_{n}}) < 1$
. So
![]() ${B_{n}}$
is not a tautology of
${B_{n}}$
is not a tautology of
![]() $\mathbf {LC}_{m}$
or
$\mathbf {LC}_{m}$
or
![]() $\mathbf {LC}$
. Since
$\mathbf {LC}$
. Since
![]() $\mathbf {H} \subsetneq \mathbf {KC} \subsetneq \mathbf {LC}$
, the result also follows for
$\mathbf {H} \subsetneq \mathbf {KC} \subsetneq \mathbf {LC}$
, the result also follows for
![]() $\mathbf {KC}{}$
and
$\mathbf {KC}{}$
and
![]() $\mathbf {H}$
.⊣
$\mathbf {H}$
.⊣
Proposition 6.4.
![]() $\mathbf {H} + {B_{m}} \vdash \mathit {Lin}$
.
$\mathbf {H} + {B_{m}} \vdash \mathit {Lin}$
.
Proof. Simultaneously substitute A for
![]() $A_{i}$
if i is odd, and B for
$A_{i}$
if i is odd, and B for
![]() $A_{i}$
if i is even in
$A_{i}$
if i is even in
![]() ${B_{m}}$
. The result is one of
${B_{m}}$
. The result is one of
 $$ \begin{align*} & (A \mathbin{\rightarrow} B) \lor (B \mathbin{\rightarrow} A) \lor \dots \lor (A \mathbin{\rightarrow} B) \text{ and}\\ & (A \mathbin{\rightarrow} B) \lor (B \mathbin{\rightarrow} A) \lor \dots \lor (B \mathbin{\rightarrow} A). \end{align*} $$
$$ \begin{align*} & (A \mathbin{\rightarrow} B) \lor (B \mathbin{\rightarrow} A) \lor \dots \lor (A \mathbin{\rightarrow} B) \text{ and}\\ & (A \mathbin{\rightarrow} B) \lor (B \mathbin{\rightarrow} A) \lor \dots \lor (B \mathbin{\rightarrow} A). \end{align*} $$
Both are equivalent in
![]() $\mathbf {H}{}$
to
$\mathbf {H}{}$
to
![]() $(A \mathbin {\rightarrow } B) \lor (B \mathbin {\rightarrow } A)$
.⊣
$(A \mathbin {\rightarrow } B) \lor (B \mathbin {\rightarrow } A)$
.⊣
Proposition 6.5. If
![]() $\mathbf {L} \vdash {B_{n}}$
, then
$\mathbf {L} \vdash {B_{n}}$
, then
![]() $\mathbf {L} = \mathbf {LC}_{m}$
for some m.
$\mathbf {L} = \mathbf {LC}_{m}$
for some m.
Proof. Hosoi [Reference Hosoi16] showed that the n-valued Gödel logic is axiomatized by
![]() $\mathbf {H} + R_{n-1}$
, where
$\mathbf {H} + R_{n-1}$
, where
![]() $R_{n}$
is
$R_{n}$
is
By simultaneously substituting
![]() $\top $
for
$\top $
for
![]() $A_{1}$
,
$A_{1}$
,
![]() $\bot $
for
$\bot $
for
![]() $A_{n+1}$
, and
$A_{n+1}$
, and
![]() $A_{i-1}$
for
$A_{i-1}$
for
![]() $A_{i}$
(
$A_{i}$
(
![]() $i = 2$
, …, n) in
$i = 2$
, …, n) in
![]() ${B_{n}}$
, we obtain
${B_{n}}$
, we obtain
which is equivalent to
![]() $R_{n-1}$
in
$R_{n-1}$
in
![]() $\mathbf {H}$
. Hence, since
$\mathbf {H}$
. Hence, since
![]() $\mathbf {L} \vdash {B_{n}}$
,
$\mathbf {L} \vdash {B_{n}}$
,
![]() $\mathbf {LC}_{n} \subseteq \mathbf {L}$
.
$\mathbf {LC}_{n} \subseteq \mathbf {L}$
.
Furthermore, Hosoi [Reference Hosoi17, Lemma 4.1] showed that if
![]() $\mathbf {L} \vdash \mathit {Lin}$
then
$\mathbf {L} \vdash \mathit {Lin}$
then
![]() $\mathbf {L} = \mathbf {LC}_{m}$
for some m or
$\mathbf {L} = \mathbf {LC}_{m}$
for some m or
![]() $L = \mathbf {LC}$
. Since
$L = \mathbf {LC}$
. Since
![]() $\mathbf {L} \vdash {B_{n}}$
,
$\mathbf {L} \vdash {B_{n}}$
,
![]() $\mathbf {L} \vdash \mathit {Lin}$
by Proposition 6.4. The result follows as
$\mathbf {L} \vdash \mathit {Lin}$
by Proposition 6.4. The result follows as
![]() $\mathbf {LC} \nvdash {B_{n}}$
and so
$\mathbf {LC} \nvdash {B_{n}}$
and so
![]() $\mathbf {L} \neq \mathbf {LC}$
.Footnote
7
⊣
$\mathbf {L} \neq \mathbf {LC}$
.Footnote
7
⊣
Corollary 6.6. No intermediate logic except
![]() $\mathbf {LC}_{m}$
has the extended first
$\mathbf {LC}_{m}$
has the extended first
![]() ${\varepsilon \tau }$
-theorem. In particular, intuitionistic logic
${\varepsilon \tau }$
-theorem. In particular, intuitionistic logic
![]() $\mathbf {H}$
, Jankov logic
$\mathbf {H}$
, Jankov logic
![]() $\mathbf {KC}$
, and infinite-valued Gödel logic
$\mathbf {KC}$
, and infinite-valued Gödel logic
![]() $\mathbf {LC}{}$
do not have the extended first
$\mathbf {LC}{}$
do not have the extended first
![]() ${\varepsilon \tau }$
-theorem.
${\varepsilon \tau }$
-theorem.
We have restricted
![]() $\mathbf {L}$
here to be an intermediate propositional logic. However, it bears remarking that Theorem 6.2 does not require that
$\mathbf {L}$
here to be an intermediate propositional logic. However, it bears remarking that Theorem 6.2 does not require that
![]() $\mathbf {L}$
contains
$\mathbf {L}$
contains
![]() $\mathbf {H}$
. An inspection of the proof shows that all that is required is that
$\mathbf {H}$
. An inspection of the proof shows that all that is required is that
![]() $\mathbf {L} \vdash A \mathbin {\rightarrow } A$
, and in
$\mathbf {L} \vdash A \mathbin {\rightarrow } A$
, and in
![]() $\mathbf {L}$
,
$\mathbf {L}$
,
![]() $\lor $
is provably commutative, associative, and idempotent, and has weakening (
$\lor $
is provably commutative, associative, and idempotent, and has weakening (
![]() $\mathbf {L} \vdash A \mathbin {\rightarrow } (A \lor B)$
). Thus, Corollary 6.6 applies to any
$\mathbf {L} \vdash A \mathbin {\rightarrow } (A \lor B)$
). Thus, Corollary 6.6 applies to any
![]() ${\varepsilon \tau }$
-calculus based on a logic which has these properties (such as, say, Łukasiewicz logic).
${\varepsilon \tau }$
-calculus based on a logic which has these properties (such as, say, Łukasiewicz logic).
The extended first
![]() $\varepsilon $
-theorem in classical logic shows that if an existential formula
$\varepsilon $
-theorem in classical logic shows that if an existential formula
![]() $\exists x\,A(x)$
is provable, so is a disjunction of instances
$\exists x\,A(x)$
is provable, so is a disjunction of instances
![]() $\bigvee _{i} A(t_{i})$
. Clearly this is equivalent to: if
$\bigvee _{i} A(t_{i})$
. Clearly this is equivalent to: if
![]() $\forall x\,A(x) \mathbin {\rightarrow } B$
is provable so is
$\forall x\,A(x) \mathbin {\rightarrow } B$
is provable so is
![]() $\bigwedge A(t_{i}) \mathbin {\rightarrow } B$
. Without the interdefinability of
$\bigwedge A(t_{i}) \mathbin {\rightarrow } B$
. Without the interdefinability of
![]() $\forall $
and
$\forall $
and
![]() $\exists $
, the question arises whether the alternative form of the
$\exists $
, the question arises whether the alternative form of the
![]() $\varepsilon $
-theorem might hold in an intermediate
$\varepsilon $
-theorem might hold in an intermediate
![]() ${\varepsilon \tau }$
-calculus even if the standard form does not. We’ll show that the versions are, in fact, equivalent even in intermediate logics.
${\varepsilon \tau }$
-calculus even if the standard form does not. We’ll show that the versions are, in fact, equivalent even in intermediate logics.
Proposition 6.7. The following are equivalent
![]() $:$
$:$
-
1. If
 $\mathbf {L}{\varepsilon \tau } \vdash A(e)$
then
$\mathbf {L}{\varepsilon \tau } \vdash A(e)$
then
 $\mathbf {L} \vdash \bigvee _{i} A(t)$
.
$\mathbf {L} \vdash \bigvee _{i} A(t)$
. -
2. If
 $B(e^{\prime }) \vdash _{\mathbf {L}{\varepsilon \tau }} C$
then
$B(e^{\prime }) \vdash _{\mathbf {L}{\varepsilon \tau }} C$
then
 $\bigwedge _{j} B(s_{j}) \vdash _{\mathbf {L}} C$
for
$\bigwedge _{j} B(s_{j}) \vdash _{\mathbf {L}} C$
for
 $C\ {\varepsilon \tau }$
-free.
$C\ {\varepsilon \tau }$
-free. -
3. If
 $B(e^{\prime }) \vdash _{\mathbf {L}{\varepsilon \tau }} C(e)$
then
$B(e^{\prime }) \vdash _{\mathbf {L}{\varepsilon \tau }} C(e)$
then
 $\bigwedge _{j} B(s_{j}) \vdash _{\mathbf {L}} \bigvee _{i} C(t_{i})$
.
$\bigwedge _{j} B(s_{j}) \vdash _{\mathbf {L}} \bigvee _{i} C(t_{i})$
.
Proof. (1) implies (3): Suppose
By the deduction theorem,
By (1) we have terms
![]() ${s_{i}, t_{i}}$
so that
${s_{i}, t_{i}}$
so that
By intuitionistic logic,
 $$ \begin{align*} & \vdash \bigwedge_{i} B(s_{i}) \mathbin{\rightarrow} \bigvee_{i} C(t_{i}) \text{ and so}\\ \bigwedge_{i} B(s_{i}) & \vdash \bigvee_{i} C(t_{i}), \end{align*} $$
$$ \begin{align*} & \vdash \bigwedge_{i} B(s_{i}) \mathbin{\rightarrow} \bigvee_{i} C(t_{i}) \text{ and so}\\ \bigwedge_{i} B(s_{i}) & \vdash \bigvee_{i} C(t_{i}), \end{align*} $$
by the deduction theorem.
(3) clearly implies (1) and (2).
(2) implies (1): Let X be a propositional variable.
![]() $A \vdash _{\mathbf {H}} (A \mathbin {\rightarrow } X) \mathbin {\rightarrow } X$
. So if
$A \vdash _{\mathbf {H}} (A \mathbin {\rightarrow } X) \mathbin {\rightarrow } X$
. So if
![]() $\mathbf {L}{\varepsilon \tau } \vdash A(e)$
then by the deduction theorem,
$\mathbf {L}{\varepsilon \tau } \vdash A(e)$
then by the deduction theorem,
 $$ \begin{align*} A(e) \mathbin{\rightarrow} X & \vdash_{\mathbf{L}{\varepsilon\tau}} X \text{ and by (2),}\\ \bigwedge_{i} (A(s_{i}) \mathbin{\rightarrow} X) & \vdash_{\mathbf{L}} X. \end{align*} $$
$$ \begin{align*} A(e) \mathbin{\rightarrow} X & \vdash_{\mathbf{L}{\varepsilon\tau}} X \text{ and by (2),}\\ \bigwedge_{i} (A(s_{i}) \mathbin{\rightarrow} X) & \vdash_{\mathbf{L}} X. \end{align*} $$
Now substitute
![]() $\bigvee _{i} A(s_{i})$
for X:
$\bigvee _{i} A(s_{i})$
for X:
The formula on the left is provable intuitionistically.⊣
7 Elimination sets and excluded middle
The basic idea of Hilbert’s proof of the extended first
![]() $\varepsilon $
-theorem is this: Suppose we have a proof of
$\varepsilon $
-theorem is this: Suppose we have a proof of
![]() $E \equiv D(e)$
from critical formulas
$E \equiv D(e)$
from critical formulas
![]() $\Gamma , \Lambda (e)$
, where e is a critical
$\Gamma , \Lambda (e)$
, where e is a critical
![]() $\varepsilon $
-term and
$\varepsilon $
-term and
![]() $\Lambda (e)$
is a set of critical formulas belonging to e. Now we find terms
$\Lambda (e)$
is a set of critical formulas belonging to e. Now we find terms
![]() $t_{1}$
, …,
$t_{1}$
, …,
![]() $t_{k}$
such that replacing e by
$t_{k}$
such that replacing e by
![]() $t_{i}$
allows us to remove the critical formulas
$t_{i}$
allows us to remove the critical formulas
![]() $\Lambda (e)$
, while at the same time replacing the end-formula
$\Lambda (e)$
, while at the same time replacing the end-formula
![]() $D(e)$
by
$D(e)$
by
![]() $\bigvee _{i=1}^{k} D(t_{i})$
and the remaining critical formulas by
$\bigvee _{i=1}^{k} D(t_{i})$
and the remaining critical formulas by
![]() $\Gamma [t_{1}/e]$
, …,
$\Gamma [t_{1}/e]$
, …,
![]() $\Gamma [t_{k}/e]$
. We repeat this procedure in such a way that eventually all critical formulas are removed and we are left with a disjunction of instances of E, as required by the first
$\Gamma [t_{k}/e]$
. We repeat this procedure in such a way that eventually all critical formulas are removed and we are left with a disjunction of instances of E, as required by the first
![]() $\varepsilon $
-theorem. The difficulty of making this work lies in three challenges. The first is to find a suitable way of selecting
$\varepsilon $
-theorem. The difficulty of making this work lies in three challenges. The first is to find a suitable way of selecting
![]() $\varepsilon $
-terms e and corresponding critical formulas
$\varepsilon $
-terms e and corresponding critical formulas
![]() $\Lambda (e)$
so that the
$\Lambda (e)$
so that the
![]() $\Lambda (e)$
can be removed. The second is to ensure that in passing from
$\Lambda (e)$
can be removed. The second is to ensure that in passing from
![]() $\Gamma $
to
$\Gamma $
to
![]() $\Gamma [t_{i}/e]$
we again obtain critical formulas.Footnote
8
The third challenge is to guarantee that the process eventually terminates with no critical formulas remaining.
$\Gamma [t_{i}/e]$
we again obtain critical formulas.Footnote
8
The third challenge is to guarantee that the process eventually terminates with no critical formulas remaining.
In this section we address the first challenge by considering the condition that suffices to overcome it: the existence of complete e-elimination sets (defined below) for every
![]() ${\varepsilon \tau }$
-term e. We then show why this condition is satisfied in classical logic, so we can clarify the role of excluded middle in the proof for the classical case, as well as how the proof for classical logic and those for intermediate logics given later correspond to one another. We will discuss the condition for intermediate logics in Section 8 and the remaining challenges in Section 9.
${\varepsilon \tau }$
-term e. We then show why this condition is satisfied in classical logic, so we can clarify the role of excluded middle in the proof for the classical case, as well as how the proof for classical logic and those for intermediate logics given later correspond to one another. We will discuss the condition for intermediate logics in Section 8 and the remaining challenges in Section 9.
Definition 7.1. Suppose
![]() $\Gamma \vdash _{\mathbf {L}{\varepsilon \tau }}^{\pi } D$
with critical formulas
$\Gamma \vdash _{\mathbf {L}{\varepsilon \tau }}^{\pi } D$
with critical formulas
![]() $\Gamma $
, and e is an
$\Gamma $
, and e is an
![]() $\varepsilon $
-term
$\varepsilon $
-term
![]() $\varepsilon _{x}\,A(x)$
(
$\varepsilon _{x}\,A(x)$
(
![]() $\tau $
-term
$\tau $
-term
![]() $\tau _{x}\,A(x)$
). If
$\tau _{x}\,A(x)$
). If
![]() $C\equiv A(t) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x)) \in \Gamma $
(
$C\equiv A(t) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x)) \in \Gamma $
(
![]() $C \equiv A(\tau _{x}\,A(x)) \mathbin {\rightarrow } A(t) \in \Gamma $
) we say e is the critical
$C \equiv A(\tau _{x}\,A(x)) \mathbin {\rightarrow } A(t) \in \Gamma $
) we say e is the critical
![]() ${\varepsilon \tau }$
-term of C, that e belongs to C, and that e is a critical
${\varepsilon \tau }$
-term of C, that e belongs to C, and that e is a critical
![]() ${\varepsilon \tau }$
-term of
${\varepsilon \tau }$
-term of
![]() $\pi $
.
$\pi $
.
Definition 7.2. Suppose
![]() $\Gamma , \Lambda (e), \Lambda ^{\prime }(e) \vdash _{\mathbf {L}{\varepsilon \tau }}^{\pi } D(e)$
where
$\Gamma , \Lambda (e), \Lambda ^{\prime }(e) \vdash _{\mathbf {L}{\varepsilon \tau }}^{\pi } D(e)$
where
![]() $\Lambda (e) \cup \Lambda (e)^{\prime }$
are all critical formulas belonging to e. A set of terms
$\Lambda (e) \cup \Lambda (e)^{\prime }$
are all critical formulas belonging to e. A set of terms
![]() $s_{1}$
, …,
$s_{1}$
, …,
![]() $s_{k}$
is an e-elimination set for
$s_{k}$
is an e-elimination set for
![]() $\pi $
and
$\pi $
and
![]() $\Lambda (e)$
if
$\Lambda (e)$
if
If
![]() $\Lambda (e)$
is the set of all critical formulas belonging to e (i.e.,
$\Lambda (e)$
is the set of all critical formulas belonging to e (i.e.,
![]() $\Lambda ^{\prime }(e) = \emptyset $
) then an e-elimination set for
$\Lambda ^{\prime }(e) = \emptyset $
) then an e-elimination set for
![]() $\Lambda (e)$
is called a complete e-elimination set.
$\Lambda (e)$
is called a complete e-elimination set.
Here,
![]() $\Gamma [s_{i}/e]$
means the result of replacing, in each formula in
$\Gamma [s_{i}/e]$
means the result of replacing, in each formula in
![]() $\Gamma $
, every occurrence of e by
$\Gamma $
, every occurrence of e by
![]() $s_{i}$
. If
$s_{i}$
. If
![]() $T = \{s_{1}, \dots , s_{k}\}$
we write
$T = \{s_{1}, \dots , s_{k}\}$
we write
![]() $\Gamma [T]$
for
$\Gamma [T]$
for
![]() $\Gamma [s_{1}]$
, …,
$\Gamma [s_{1}]$
, …,
![]() $\Gamma [s_{k}]$
. Note that we do not require in the definition of e-elimination sets that the formulas in
$\Gamma [s_{k}]$
. Note that we do not require in the definition of e-elimination sets that the formulas in
![]() $\Gamma [s_{i}/e]$
are actually critical formulas.
$\Gamma [s_{i}/e]$
are actually critical formulas.
Lemma 7.3. If
![]() $C \equiv A(t) \mathbin {\rightarrow } A(e)$
or
$C \equiv A(t) \mathbin {\rightarrow } A(e)$
or
![]() $C \equiv A(e) \mathbin {\rightarrow } A(t)$
is a critical formula with critical
$C \equiv A(e) \mathbin {\rightarrow } A(t)$
is a critical formula with critical
![]() ${\varepsilon \tau }$
-term e, then
${\varepsilon \tau }$
-term e, then
![]() $C[s/e]$
is
$C[s/e]$
is
![]() $A(t[s/e]) \mathbin {\rightarrow } A(s)$
or
$A(t[s/e]) \mathbin {\rightarrow } A(s)$
or
![]() $A(s) \mathbin {\rightarrow } A(t[s/e])$
, respectively.
$A(s) \mathbin {\rightarrow } A(t[s/e])$
, respectively.
Proof. Since e is the critical
![]() $\varepsilon $
-term of C,
$\varepsilon $
-term of C,
![]() $e \equiv \varepsilon _{x}\,A(x)$
or
$e \equiv \varepsilon _{x}\,A(x)$
or
![]() $e \equiv \tau _{x}\,A(x)$
. Hence, e cannot occur in
$e \equiv \tau _{x}\,A(x)$
. Hence, e cannot occur in
![]() $A(x)$
, since otherwise it would be a proper subterm of itself.⊣
$A(x)$
, since otherwise it would be a proper subterm of itself.⊣
Lemma 7.4. If
![]() $\Gamma \vdash _{\mathbf {L}} D$
then
$\Gamma \vdash _{\mathbf {L}} D$
then
![]() $\Gamma [t/e] \vdash _{\mathbf {L}} D[t/e]$
.
$\Gamma [t/e] \vdash _{\mathbf {L}} D[t/e]$
.
Proof. Any proof of D from
![]() $\Gamma $
using modus ponens and axioms of
$\Gamma $
using modus ponens and axioms of
![]() $\mathbf {L}$
remains correct if terms in it are uniformly replaced by other terms.⊣
$\mathbf {L}$
remains correct if terms in it are uniformly replaced by other terms.⊣
Lemma 7.5. In any intermediate logic
![]() $\mathbf {L}:$
$\mathbf {L}:$
-
1. If
 $\Gamma , A \vdash C$
and
$\Gamma , A \vdash C$
and
 $\Gamma ^{\prime }, B \vdash _{\mathbf {L}} D$
then
$\Gamma ^{\prime }, B \vdash _{\mathbf {L}} D$
then
 $\Gamma , \Gamma ^{\prime }, A \lor B \vdash C \lor D$
.
$\Gamma , \Gamma ^{\prime }, A \lor B \vdash C \lor D$
. -
2. If
 $\Gamma , A \vdash _{\mathbf {L}} C$
and
$\Gamma , A \vdash _{\mathbf {L}} C$
and
 $B \vdash A$
, then
$B \vdash A$
, then
 $\Gamma , B \vdash C$
.
$\Gamma , B \vdash C$
.
We are now in a position to apply the preceding lemmas and the concept of elimination sets to the case of classical logic. This elucidates how the first challenge is solved in the proof of the extended first
![]() ${\varepsilon \tau }$
-theorem for classical logic where
${\varepsilon \tau }$
-theorem for classical logic where
![]() $\tau $
-terms and corresponding critical formulas may also be present. (For Hilbert’s original proof for the
$\tau $
-terms and corresponding critical formulas may also be present. (For Hilbert’s original proof for the
![]() $\varepsilon $
-calculus without
$\varepsilon $
-calculus without
![]() $\tau $
-terms, see [Reference Hilbert and Bernays15] or [Reference Moser and Zach23].)
$\tau $
-terms, see [Reference Hilbert and Bernays15] or [Reference Moser and Zach23].)
Proposition 7.6. In
![]() $\mathbf {C}{\varepsilon \tau }$
, every critical formula
$\mathbf {C}{\varepsilon \tau }$
, every critical formula
![]() $C(e)$
has an e-elimination set.
$C(e)$
has an e-elimination set.
Proof. Suppose first that e is an
![]() $\varepsilon $
-term; then
$\varepsilon $
-term; then
![]() $C(e)$
is
$C(e)$
is
![]() $A(s) \mathbin {\rightarrow } A(e)$
. Let
$A(s) \mathbin {\rightarrow } A(e)$
. Let
![]() $\Lambda ^{\prime }(e)$
be the critical formulas belonging to e other than
$\Lambda ^{\prime }(e)$
be the critical formulas belonging to e other than
![]() $C(e)$
, and
$C(e)$
, and
![]() $\Gamma $
the remaining critical formulas for which e is not critical. So we have:
$\Gamma $
the remaining critical formulas for which e is not critical. So we have:
On the one hand, by replacing e everywhere by s we get
and by Lemma 7.5(2), since A(s)
![]() $\vdash A(t[s/e]) \mathbin {\rightarrow } A(s) \in \Lambda ^{\prime }(s)$
and
$\vdash A(t[s/e]) \mathbin {\rightarrow } A(s) \in \Lambda ^{\prime }(s)$
and
![]() $A(s) \vdash C(s)$
,
$A(s) \vdash C(s)$
,
On the other hand, since
![]() $\lnot A(s) \vdash A(s) \mathbin {\rightarrow } A(e)$
,
$\lnot A(s) \vdash A(s) \mathbin {\rightarrow } A(e)$
,
 $$ \begin{align*} \Gamma, \lnot A(s) & \vdash_{\mathbf{C}} D(e) \text{ and so,}\\ \Gamma, \Gamma[s/e], A(s) \lor \lnot A(s)& \vdash_{\mathbf{C}} D(e) \lor D(s), \end{align*} $$
$$ \begin{align*} \Gamma, \lnot A(s) & \vdash_{\mathbf{C}} D(e) \text{ and so,}\\ \Gamma, \Gamma[s/e], A(s) \lor \lnot A(s)& \vdash_{\mathbf{C}} D(e) \lor D(s), \end{align*} $$
by Lemma 7.5(1). Since
![]() $\mathbf {C} \vdash A(s) \lor \lnot A(s)$
we have
$\mathbf {C} \vdash A(s) \lor \lnot A(s)$
we have
Thus,
![]() $\{e, s\}$
is an e-elimination set for the critical formula
$\{e, s\}$
is an e-elimination set for the critical formula
![]() $C(e)$
.
$C(e)$
.
Similarly, if e is a
![]() ${\tau }$
-term and
${\tau }$
-term and
![]() $C(e)$
is
$C(e)$
is
![]() $A(e) \mathbin {\rightarrow } A(s)$
we get
$A(e) \mathbin {\rightarrow } A(s)$
we get
and by Lemma 7.5(2), since
![]() $\lnot A(s) \vdash C^{\prime } \in \Lambda ^{\prime }(e)$
and
$\lnot A(s) \vdash C^{\prime } \in \Lambda ^{\prime }(e)$
and
![]() $\lnot A(s) \vdash C(s)$
,
$\lnot A(s) \vdash C(s)$
,
On the other hand,
![]() $A(s) \vdash C(e)$
, so
$A(s) \vdash C(e)$
, so
 $$ \begin{align*} \Gamma, A(s) & \vdash_{\mathbf{C}} D(e) \text{ and}\\ \Gamma, \Gamma[s/e], \lnot A(s) \lor A(s)& \vdash_{\mathbf{C}} D(e) \lor D(s), \end{align*} $$
$$ \begin{align*} \Gamma, A(s) & \vdash_{\mathbf{C}} D(e) \text{ and}\\ \Gamma, \Gamma[s/e], \lnot A(s) \lor A(s)& \vdash_{\mathbf{C}} D(e) \lor D(s), \end{align*} $$
More generally, the set of all critical formulas belonging to e has a (complete) e-elimination set in
![]() $\mathbf {C}$
:
$\mathbf {C}$
:
Proposition 7.7. In
![]() $\mathbf {C}{\varepsilon \tau }$
, every critical
$\mathbf {C}{\varepsilon \tau }$
, every critical
![]() ${\varepsilon \tau }$
-term has a complete e-elimination set.
${\varepsilon \tau }$
-term has a complete e-elimination set.
Proof. Let
![]() $C_{1} \equiv A(s_{1}) \mathbin {\rightarrow } A(e)$
, …,
$C_{1} \equiv A(s_{1}) \mathbin {\rightarrow } A(e)$
, …,
![]() $C_{k} \equiv A(s_{k}) \mathbin {\rightarrow } A(e)$
be the critical formulas belonging to e if e is an
$C_{k} \equiv A(s_{k}) \mathbin {\rightarrow } A(e)$
be the critical formulas belonging to e if e is an
![]() $\varepsilon $
-term. Since
$\varepsilon $
-term. Since
 $$ \begin{align*} \Gamma, C_{1}(e), \dots, C_{k}(e) & \vdash_{\mathbf{C}} D(e) \text{, also}\\ \Gamma[s_{i}/e], C_{1}(s_{i}), \dots, C_{k}(s_{i}) & \vdash_{\mathbf{C}} D(s_{i}) \end{align*} $$
$$ \begin{align*} \Gamma, C_{1}(e), \dots, C_{k}(e) & \vdash_{\mathbf{C}} D(e) \text{, also}\\ \Gamma[s_{i}/e], C_{1}(s_{i}), \dots, C_{k}(s_{i}) & \vdash_{\mathbf{C}} D(s_{i}) \end{align*} $$
(writing
![]() ${C_{j}(s_{i})}$
for
${C_{j}(s_{i})}$
for
![]() ${C_{j}[s_{i}/e]}$
). Since
${C_{j}[s_{i}/e]}$
). Since
![]() ${A(s_{i}) \vdash A(s_{j}(s_{i})) \mathbin {\rightarrow } A(s_{i}) \equiv C_{j}(s_{i})}$
,
${A(s_{i}) \vdash A(s_{j}(s_{i})) \mathbin {\rightarrow } A(s_{i}) \equiv C_{j}(s_{i})}$
,
by Lemma 7.5(2). By applying Lemma 7.5(1),
On the other hand, since
![]() ${\lnot A(s_{i}) \vdash A(s_{i}) \mathbin {\rightarrow } A(e)}$
, we get
${\lnot A(s_{i}) \vdash A(s_{i}) \mathbin {\rightarrow } A(e)}$
, we get
![]() $\lnot A(s_{1}) \land \cdots \land \lnot A(s_{k}) \vdash C_{j}(e)$
for each
$\lnot A(s_{1}) \land \cdots \land \lnot A(s_{k}) \vdash C_{j}(e)$
for each
![]() ${j = 1, \dots , \textit {k}}$
, so we also have, from the first line by Lemma 7.5(2),
${j = 1, \dots , \textit {k}}$
, so we also have, from the first line by Lemma 7.5(2),
Since
![]() ${\bigvee _{i} A(s_{i}) \lor (\bigwedge _{i} \lnot A(s_{i}))}$
is an instance of excluded middle, we have
${\bigvee _{i} A(s_{i}) \lor (\bigwedge _{i} \lnot A(s_{i}))}$
is an instance of excluded middle, we have
If e is a
![]() $\tau $
-term, then the critical formulas are of the form
$\tau $
-term, then the critical formulas are of the form
![]() $C_{j}(e) \equiv A(e) \mathbin {\rightarrow } A(s_{j}(e))$
and consequently
$C_{j}(e) \equiv A(e) \mathbin {\rightarrow } A(s_{j}(e))$
and consequently
![]() $C_{j}(s_{i})$
is
$C_{j}(s_{i})$
is
![]() $A(s_{i}) \mathbin {\rightarrow } A(s_{j}(s_{i}))$
. Each is implied by
$A(s_{i}) \mathbin {\rightarrow } A(s_{j}(s_{i}))$
. Each is implied by
![]() $\lnot A(s_{i})$
, so we have
$\lnot A(s_{i})$
, so we have
On the other hand,
![]() $A(s_{1}) \land \dots \land A(s_{k}) \vdash A(e) \mathbin {\rightarrow } A(s_{j})$
, so
$A(s_{1}) \land \dots \land A(s_{k}) \vdash A(e) \mathbin {\rightarrow } A(s_{j})$
, so
and consequently
since
![]() $\bigwedge _{i} A(s_{i}) \lor \bigvee _{i} \lnot A(s_{i})$
is a tautology.
$\bigwedge _{i} A(s_{i}) \lor \bigvee _{i} \lnot A(s_{i})$
is a tautology.
In each case,
![]() $\{e, s_{1}, \dots , s_{k}\}$
is an e-elimination set.⊣
$\{e, s_{1}, \dots , s_{k}\}$
is an e-elimination set.⊣
Remark 7.8. Of course, the fact that in
![]() $\mathbf {C}{}$
we have complete e-elimination sets can also be obtained by applying Proposition 7.6 k-many times. Applying it to
$\mathbf {C}{}$
we have complete e-elimination sets can also be obtained by applying Proposition 7.6 k-many times. Applying it to
![]() $C_{1}(e)$
results in
$C_{1}(e)$
results in
![]() $T_{1} = \{e, s_{1}(e)\}$
, applying it to
$T_{1} = \{e, s_{1}(e)\}$
, applying it to
![]() $C_{2}(e)$
in
$C_{2}(e)$
in
![]() $T_{2} = \{e, s_{1}(e), s_{2}(e), s_{1}(s_{2}(e))\}$
, to
$T_{2} = \{e, s_{1}(e), s_{2}(e), s_{1}(s_{2}(e))\}$
, to
![]() $C_{3}$
in
$C_{3}$
in
![]() $T_{3} = \{e, s_{1}(e), s_{2}(e), s_{1}(s_{2}(e)), s_{3}(e), s_{1}(s_{3}(e)), s_{2}(s_{3}(e)), s_{1}(s_{2}(s_{3}(e)))\}$
, etc., i.e., the resulting disjunction has
$T_{3} = \{e, s_{1}(e), s_{2}(e), s_{1}(s_{2}(e)), s_{3}(e), s_{1}(s_{3}(e)), s_{2}(s_{3}(e)), s_{1}(s_{2}(s_{3}(e)))\}$
, etc., i.e., the resulting disjunction has
![]() $2^{k+1}$
disjuncts, whereas the disjunction resulting from Proposition 7.7 only has
$2^{k+1}$
disjuncts, whereas the disjunction resulting from Proposition 7.7 only has
![]() $k+1$
disjuncts. However, see Remark 9.7.
$k+1$
disjuncts. However, see Remark 9.7.
We know that intermediate logics other than
![]() $\mathbf {LC}_{m}$
do not have the extended first
$\mathbf {LC}_{m}$
do not have the extended first
![]() ${\varepsilon \tau }$
-theorem and so not every
${\varepsilon \tau }$
-theorem and so not every
![]() ${\varepsilon \tau }$
-term will have complete e-elimination sets. However, if the starting formula E is of a special form, they sometimes do. In the proof for the classical case above, this required excluded middle. But it need not. For instance, if E is negated, then weak excluded middle (
${\varepsilon \tau }$
-term will have complete e-elimination sets. However, if the starting formula E is of a special form, they sometimes do. In the proof for the classical case above, this required excluded middle. But it need not. For instance, if E is negated, then weak excluded middle (
![]() $\lnot A \lor \lnot \lnot A$
) is enough.
$\lnot A \lor \lnot \lnot A$
) is enough.
Proposition 7.9. If
![]() $\mathbf {L} \vdash J$
, then every
$\mathbf {L} \vdash J$
, then every
![]() ${\varepsilon \tau }$
-term in an
${\varepsilon \tau }$
-term in an
![]() $\mathbf {L}{\varepsilon \tau }$
-proof of
$\mathbf {L}{\varepsilon \tau }$
-proof of
![]() $\bigvee _{j} \lnot D_{j}$
has a complete e-elimination set.
$\bigvee _{j} \lnot D_{j}$
has a complete e-elimination set.
Proof. Let
![]() $C_{1} \equiv A(s_{1}) \mathbin {\rightarrow } A(e)$
, …,
$C_{1} \equiv A(s_{1}) \mathbin {\rightarrow } A(e)$
, …,
![]() $C_{k} \equiv A(s_{k}) \mathbin {\rightarrow } A(e)$
be the critical formulas belonging to e if e is an
$C_{k} \equiv A(s_{k}) \mathbin {\rightarrow } A(e)$
be the critical formulas belonging to e if e is an
![]() $\varepsilon $
-term. As before, we have
$\varepsilon $
-term. As before, we have
In
![]() ${\mathbf {KC}, B \mathbin {\rightarrow } (\lnot C_{1} \lor \lnot C_{2}) \vdash \lnot \lnot B \mathbin {\rightarrow } (\lnot C_{1} \lor \lnot C_{2})}$
, so
${\mathbf {KC}, B \mathbin {\rightarrow } (\lnot C_{1} \lor \lnot C_{2}) \vdash \lnot \lnot B \mathbin {\rightarrow } (\lnot C_{1} \lor \lnot C_{2})}$
, so
We obtain
 $$ \begin{align*} \Gamma[s_{1}/e], \dots, \Gamma[s_{k}/e], &\\ \lnot \lnot A(s_{1}) \lor \dots \lor \lnot\lnot A(s_{k}) & \vdash_{\mathbf{L}} \bigvee_{j} \lnot D_{j}(s_{1}) \lor \dots \lor \bigvee_{j} \lnot D_{j}(s_{k}). \end{align*} $$
$$ \begin{align*} \Gamma[s_{1}/e], \dots, \Gamma[s_{k}/e], &\\ \lnot \lnot A(s_{1}) \lor \dots \lor \lnot\lnot A(s_{k}) & \vdash_{\mathbf{L}} \bigvee_{j} \lnot D_{j}(s_{1}) \lor \dots \lor \bigvee_{j} \lnot D_{j}(s_{k}). \end{align*} $$
Again as before, we have
and together
 $$ \begin{align*} \Gamma[s_{1}/e], \dots, \Gamma[s_{k}/e], \Gamma, &\\ (\lnot A(s_{1}) \land \cdots \land \lnot A(s_{k})) \lor {} &\\ \lnot \lnot A(s_{1}) \lor \dots \lor \lnot\lnot A(s_{k}) & \vdash_{\mathbf{L}} \bigvee_{j} \lnot D_{j}(e) \lor \bigvee_{j} \lnot D_{j}(s_{1}) \lor \dots \lor \bigvee_{j} \lnot D_{j}(s_{k}). \end{align*} $$
$$ \begin{align*} \Gamma[s_{1}/e], \dots, \Gamma[s_{k}/e], \Gamma, &\\ (\lnot A(s_{1}) \land \cdots \land \lnot A(s_{k})) \lor {} &\\ \lnot \lnot A(s_{1}) \lor \dots \lor \lnot\lnot A(s_{k}) & \vdash_{\mathbf{L}} \bigvee_{j} \lnot D_{j}(e) \lor \bigvee_{j} \lnot D_{j}(s_{1}) \lor \dots \lor \bigvee_{j} \lnot D_{j}(s_{k}). \end{align*} $$
Since
is provable from weak excluded middle, the claim is proved.⊣
8 Elimination sets using
 ${B_{m}}$
and
${B_{m}}$
and
 $\mathit {Lin}$
$\mathit {Lin}$
We’ve showed in Theorem 6.2 that the provability of
![]() ${B_{m}}$
for some
${B_{m}}$
for some
![]() $m \ge 2$
is a necessary condition for an intermediate logic to have the extended first
$m \ge 2$
is a necessary condition for an intermediate logic to have the extended first
![]() ${\varepsilon \tau }$
-theorem. In this section, we show that it is also sufficient: if
${\varepsilon \tau }$
-theorem. In this section, we show that it is also sufficient: if
![]() $\mathbf {L} \vdash B_{m}$
for some m, then every critical
$\mathbf {L} \vdash B_{m}$
for some m, then every critical
![]() ${\varepsilon \tau }$
-term has a complete e-elimination set.
${\varepsilon \tau }$
-term has a complete e-elimination set.
We use the notion of e-elimination sets developed in Section 7: the existence of an e-elimination set for a set of critical formulas
![]() $\Lambda $
guarantees that these critical formulas can be removed from a proof, while the end-formula is replaced by a disjunction of instances of the original end-formula. The proofs of the existence of e-elimination sets proceed by replacing an
$\Lambda $
guarantees that these critical formulas can be removed from a proof, while the end-formula is replaced by a disjunction of instances of the original end-formula. The proofs of the existence of e-elimination sets proceed by replacing an
![]() ${\varepsilon \tau }$
-term e in such a way that the disjunction of formulas
${\varepsilon \tau }$
-term e in such a way that the disjunction of formulas
![]() $\Lambda ^{\prime }$
resulting from such replacements become (provable from) tautologies in the underlying propositional logic. In Proposition 7.6, we showed how to do this for a single critical formula
$\Lambda ^{\prime }$
resulting from such replacements become (provable from) tautologies in the underlying propositional logic. In Proposition 7.6, we showed how to do this for a single critical formula
![]() $A(s) \mathbin {\rightarrow } A(e)$
in classical logic: We replace e first by s resulting in
$A(s) \mathbin {\rightarrow } A(e)$
in classical logic: We replace e first by s resulting in
![]() $A(s[s/e]) \mathbin {\rightarrow } A(s) \vdash D(s)$
, and then by itself (i.e., no replacement), resulting in
$A(s[s/e]) \mathbin {\rightarrow } A(s) \vdash D(s)$
, and then by itself (i.e., no replacement), resulting in
![]() $A(s) \mathbin {\rightarrow } A(e) \vdash D(e)$
. This gives
$A(s) \mathbin {\rightarrow } A(e) \vdash D(e)$
. This gives
but the formula on the left is a classical tautology. When eliminating multiple critical formulas at the same time (e.g., all critical formulas belonging to a single
![]() ${\varepsilon \tau }$
-term), the resulting tautologies are more complicated. In the original proof, they are all equivalent to excluded middle, and so the proofs do not apply to intermediate propositional logics. Below, we show how this can nevertheless be done as long as the underlying propositional logic contains
${\varepsilon \tau }$
-term), the resulting tautologies are more complicated. In the original proof, they are all equivalent to excluded middle, and so the proofs do not apply to intermediate propositional logics. Below, we show how this can nevertheless be done as long as the underlying propositional logic contains
![]() ${B_{m}}$
. We have to distinguish two kinds of critical formulas:
${B_{m}}$
. We have to distinguish two kinds of critical formulas:
Definition 8.1. A critical formula
![]() $A(s) \mathbin {\rightarrow } A(e)$
(or
$A(s) \mathbin {\rightarrow } A(e)$
(or
![]() $A(e) \mathbin {\rightarrow } A(s)$
if e is a
$A(e) \mathbin {\rightarrow } A(s)$
if e is a
![]() $\tau $
-term) is called predicative if e does not occur in s, and impredicative otherwise.Footnote
9
$\tau $
-term) is called predicative if e does not occur in s, and impredicative otherwise.Footnote
9
If all critical formulas are predicative,
![]() $\mathbf {L} \vdash \mathit {Lin}$
suffices (Lemma 8.5). If
$\mathbf {L} \vdash \mathit {Lin}$
suffices (Lemma 8.5). If
![]() $\mathbf {L} \vdash {B_{m}}$
for some m, we can eliminate the impredicative critical formulas for some
$\mathbf {L} \vdash {B_{m}}$
for some m, we can eliminate the impredicative critical formulas for some
![]() ${\varepsilon \tau }$
-term e in a similar way: by successively replacing e by suitable terms, we obtain a proof of a disjunction of instances of
${\varepsilon \tau }$
-term e in a similar way: by successively replacing e by suitable terms, we obtain a proof of a disjunction of instances of
![]() $D(e)$
from a formula provable from
$D(e)$
from a formula provable from
![]() ${B_{m}}$
. The number m determines the number of necessary replacements. Once impredicative critical formulas are removed, we can use Lemma 8.5 to remove the remaining predicative critical formulas.
${B_{m}}$
. The number m determines the number of necessary replacements. Once impredicative critical formulas are removed, we can use Lemma 8.5 to remove the remaining predicative critical formulas.
We prove the result for impredicative critical formulas first (Lemma 8.3). In preparation for the proof we first consider an example to illustrate the basic idea. Suppose
![]() $\mathbf {LC}_{3}{\varepsilon \tau } \vdash D(e)$
with the set of critical formulas
$\mathbf {LC}_{3}{\varepsilon \tau } \vdash D(e)$
with the set of critical formulas
 $$ \begin{align*} C_{s}(e) & \equiv A(s(e)) \mathbin{\rightarrow} A(e), \\[3pt] C_{t}(e) & \equiv A(t(e)) \mathbin{\rightarrow} A(e), \\ C_{u}(e) & \equiv A(u) \mathbin{\rightarrow} A(e), \\ C_{v}(e) & \equiv A(v) \mathbin{\rightarrow} A(e), \end{align*} $$
$$ \begin{align*} C_{s}(e) & \equiv A(s(e)) \mathbin{\rightarrow} A(e), \\[3pt] C_{t}(e) & \equiv A(t(e)) \mathbin{\rightarrow} A(e), \\ C_{u}(e) & \equiv A(u) \mathbin{\rightarrow} A(e), \\ C_{v}(e) & \equiv A(v) \mathbin{\rightarrow} A(e), \end{align*} $$
where terms u and v do not contain e. Let
![]() $C(e)$
be the conjunction of these critical formulas. We have
$C(e)$
be the conjunction of these critical formulas. We have
![]() $C_{s}(e), C_{t}(e), C_{u}(e), C_{v}(e) \vdash _{\mathbf {LC}_{3}} D(e)$
.
$C_{s}(e), C_{t}(e), C_{u}(e), C_{v}(e) \vdash _{\mathbf {LC}_{3}} D(e)$
.
We’ll consider sets of terms
![]() $X_{i}$
where
$X_{i}$
where
![]() $X_{0} = \{e\}$
and
$X_{0} = \{e\}$
and
![]() $X_{i+1} = \{ s(x), t(x) : x \in X_{i}\}$
. For the sake of readability we will leave out parentheses when writing these terms, e.g.,
$X_{i+1} = \{ s(x), t(x) : x \in X_{i}\}$
. For the sake of readability we will leave out parentheses when writing these terms, e.g.,
![]() $s(t(e))$
is abbreviated as
$s(t(e))$
is abbreviated as
![]() $ste$
.
$ste$
.
For every
![]() $w \in X_{1}$
we have
$w \in X_{1}$
we have
![]() $C(w) \vdash D(w)$
. So, by applying Lemma 7.5(1) twice, we get:
$C(w) \vdash D(w)$
. So, by applying Lemma 7.5(1) twice, we get:
 $$ \begin{align*} C(se) \lor C_{s}(e),&\\ C(te) \lor C_{t}(e), &\\ C_{u}(e), C_{v}(e) & \vdash_{\mathbf{LC}_{3}} D(e) \lor D(se) \lor D(te). \end{align*} $$
$$ \begin{align*} C(se) \lor C_{s}(e),&\\ C(te) \lor C_{t}(e), &\\ C_{u}(e), C_{v}(e) & \vdash_{\mathbf{LC}_{3}} D(e) \lor D(se) \lor D(te). \end{align*} $$
By distributivity, C(se)
![]() ${\lor C_{s}(e)}$
is equivalent to
${\lor C_{s}(e)}$
is equivalent to
 $$ \begin{align*} (C_{s}(se) \lor C_{s}(e)) & \land (C_{t}(se) \lor C_{s}(e)) \land {}\\ (C_{u}(se) \lor C_{s}(e)) & \land (C_{v}(se) \lor C_{s}(e)). \end{align*} $$
$$ \begin{align*} (C_{s}(se) \lor C_{s}(e)) & \land (C_{t}(se) \lor C_{s}(e)) \land {}\\ (C_{u}(se) \lor C_{s}(e)) & \land (C_{v}(se) \lor C_{s}(e)). \end{align*} $$
Thus we get
 $$ \begin{align*} C_{s}(se) \lor C_{s}(e), C_{t}(se) \lor C_{s}(e),& \\ C_{u}(se) \lor C_{s}(e), C_{v}(se) \lor C_{s}(e),& \\ C(te) \lor C_{t}(e),&\\ C_{u}(e), C_{v}(e) &\vdash_{\mathbf{LC}_{3}} D(e) \lor D(se) \lor D(te). \end{align*} $$
$$ \begin{align*} C_{s}(se) \lor C_{s}(e), C_{t}(se) \lor C_{s}(e),& \\ C_{u}(se) \lor C_{s}(e), C_{v}(se) \lor C_{s}(e),& \\ C(te) \lor C_{t}(e),&\\ C_{u}(e), C_{v}(e) &\vdash_{\mathbf{LC}_{3}} D(e) \lor D(se) \lor D(te). \end{align*} $$
We have
using
![]() $\mathit {Lin}$
. Similarly,
$\mathit {Lin}$
. Similarly,
![]() $C_{v}(e) \vdash _{\mathbf {LC}_{3}} C_{v}(se) \lor C_{s}(e)$
, so we have by Lemma 7.5(2):
$C_{v}(e) \vdash _{\mathbf {LC}_{3}} C_{v}(se) \lor C_{s}(e)$
, so we have by Lemma 7.5(2):
 $$ \begin{align*} C_{s}(se) \lor C_{s}(e), C_{t}(se) \lor C_{s}(e),& \\ C(te) \lor C_{t}(e),&\\ C_{u}(e), C_{v}(e) & \vdash_{\mathbf{LC}_{3}} D(e) \lor D(se) \lor D(te). \end{align*} $$
$$ \begin{align*} C_{s}(se) \lor C_{s}(e), C_{t}(se) \lor C_{s}(e),& \\ C(te) \lor C_{t}(e),&\\ C_{u}(e), C_{v}(e) & \vdash_{\mathbf{LC}_{3}} D(e) \lor D(se) \lor D(te). \end{align*} $$
Repeating this consideration with
![]() $C(te) \lor C_{t}(e)$
yields
$C(te) \lor C_{t}(e)$
yields
 $$ \begin{align*} C_{s}(se) \lor C_{s}(e), C_{t}(se) \lor C_{s}(e),& \\ C_{s}(te) \lor C_{t}(e), C_{t}(te) \lor C_{t}(e),& \\ C_{u}(e), C_{v}(e) &\vdash_{\mathbf{LC}_{3}} D(e) \lor D(se) \lor D(te). \end{align*} $$
$$ \begin{align*} C_{s}(se) \lor C_{s}(e), C_{t}(se) \lor C_{s}(e),& \\ C_{s}(te) \lor C_{t}(e), C_{t}(te) \lor C_{t}(e),& \\ C_{u}(e), C_{v}(e) &\vdash_{\mathbf{LC}_{3}} D(e) \lor D(se) \lor D(te). \end{align*} $$
Note that each of the four resulting disjunctions has as first disjunct a substitution instance of a critical formula of the form
![]() $C_{s}(w)$
or
$C_{s}(w)$
or
![]() $C_{t}(w)$
where
$C_{t}(w)$
where
![]() $w \in X_{1}$
.
$w \in X_{1}$
.
![]() $X_{2}$
are the terms of the form
$X_{2}$
are the terms of the form
![]() $s(w)$
and
$s(w)$
and
![]() $t(w)$
. So we can repeat the process, pairing
$t(w)$
. So we can repeat the process, pairing
![]() $C(s(w))$
with
$C(s(w))$
with
![]() $C_{s}(w)$
and
$C_{s}(w)$
and
![]() $C(t(w))$
with
$C(t(w))$
with
![]() $C_{t}(w)$
, i.e., obtaining
$C_{t}(w)$
, i.e., obtaining
![]() $C(sse) \lor C_{s}(se) \lor C_{s}(e)$
,
$C(sse) \lor C_{s}(se) \lor C_{s}(e)$
,
![]() $C(tse) \lor C_{t}(se) \lor C_{s}(e)$
, etc. In each case, after distributing and removing conjuncts of the form
$C(tse) \lor C_{t}(se) \lor C_{s}(e)$
, etc. In each case, after distributing and removing conjuncts of the form
![]() $C_{u}(w) \lor \cdots $
we are left with now eight disjunctions:
$C_{u}(w) \lor \cdots $
we are left with now eight disjunctions:
 $$ \begin{align*} & C_{s}(sse) \lor C_{s}(se) \lor C_{s}(e),\\ & C_{t}(sse) \lor C_{s}(se) \lor C_{s}(e),\\ & \vdots\\ & C_{t}(tte) \lor C_{t}(te) \lor C_{t}(e),\\ & C_{u}(e), C_{v}(e) \vdash_{\mathbf{LC}_{3}} D(e) \lor D(se) \lor D(te) \lor D(sse) \lor \dots \lor D(tte). \end{align*} $$
$$ \begin{align*} & C_{s}(sse) \lor C_{s}(se) \lor C_{s}(e),\\ & C_{t}(sse) \lor C_{s}(se) \lor C_{s}(e),\\ & \vdots\\ & C_{t}(tte) \lor C_{t}(te) \lor C_{t}(e),\\ & C_{u}(e), C_{v}(e) \vdash_{\mathbf{LC}_{3}} D(e) \lor D(se) \lor D(te) \lor D(sse) \lor \dots \lor D(tte). \end{align*} $$
It remains to show that the formulas on the right of the turnstile are provable in
![]() $\mathbf {LC}_{3}$
. First, consider a formula of the form
$\mathbf {LC}_{3}$
. First, consider a formula of the form
![]() $C_{i}(w) \lor \dots \lor C_{j}(e)$
, e.g.,
$C_{i}(w) \lor \dots \lor C_{j}(e)$
, e.g.,
 $$ \begin{align*} & C_{s}(tse) \lor C_{t}(se) \lor C_{s}(e), \text{ i.e.,}\\ & (A(stse)) \mathbin{\rightarrow} A(tse)) \lor (A(tse) \mathbin{\rightarrow} A(se)) \lor (A(se) \mathbin{\rightarrow} A(e)). \end{align*} $$
$$ \begin{align*} & C_{s}(tse) \lor C_{t}(se) \lor C_{s}(e), \text{ i.e.,}\\ & (A(stse)) \mathbin{\rightarrow} A(tse)) \lor (A(tse) \mathbin{\rightarrow} A(se)) \lor (A(se) \mathbin{\rightarrow} A(e)). \end{align*} $$
In each disjunct, the consequent equals the antecedent of the disjunct immediately to the right, i.e., it is a substitution instance of
i.e., of
![]() ${B_{3}}$
. Since
${B_{3}}$
. Since
![]() $\mathbf {LC}_{3} \vdash {B_{3}}$
, these are all provable.
$\mathbf {LC}_{3} \vdash {B_{3}}$
, these are all provable.
If we take
![]() $D^{\prime }(e)$
to be the disjunction obtained on the right, we have
$D^{\prime }(e)$
to be the disjunction obtained on the right, we have
 $$ \begin{align*} C_{u}(e), C_{v}(e) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(e) \text{ and thus also}\\ C_{u}(u), C_{v}(u) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(u) \text{ and}\\ C_{u}(v), C_{v}(u) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(v). \end{align*} $$
$$ \begin{align*} C_{u}(e), C_{v}(e) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(e) \text{ and thus also}\\ C_{u}(u), C_{v}(u) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(u) \text{ and}\\ C_{u}(v), C_{v}(u) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(v). \end{align*} $$
As
![]() ${C_{u}(u)}$
and
${C_{u}(u)}$
and
![]() ${C_{v}(v)}$
are of the form
${C_{v}(v)}$
are of the form
![]() $A \mathbin {\rightarrow } A$
this reduces to
$A \mathbin {\rightarrow } A$
this reduces to
 $$ \begin{align*} C_{u}(v) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(u) \text{ and}\\ C_{v}(u) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(v) \text{ and therefore:}\\ C_{u}(v) \lor C_{v}(u) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(u) \lor D^{\prime}(v). \end{align*} $$
$$ \begin{align*} C_{u}(v) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(u) \text{ and}\\ C_{v}(u) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(v) \text{ and therefore:}\\ C_{u}(v) \lor C_{v}(u) & \vdash_{\mathbf{LC}_{3}} D^{\prime}(u) \lor D^{\prime}(v). \end{align*} $$
But
![]() $C_{u}(v) \lor C_{v}(u)$
is an instance of
$C_{u}(v) \lor C_{v}(u)$
is an instance of
![]() $\mathit {Lin}$
.
$\mathit {Lin}$
.
Lemma 8.2. If
![]() $\mathbf {L} \vdash \mathit {Lin}$
, then for all m,
$\mathbf {L} \vdash \mathit {Lin}$
, then for all m,
Proof. By induction on m. If
![]() $m=1$
, this amounts to the claim:
$m=1$
, this amounts to the claim:
![]() $A_{1} \mathbin {\rightarrow } A_{2} \vdash _{\mathbf {L}} A_{1} \mathbin {\rightarrow } A_{2}$
, which is trivial. Now suppose the claim holds for m. Then
$A_{1} \mathbin {\rightarrow } A_{2} \vdash _{\mathbf {L}} A_{1} \mathbin {\rightarrow } A_{2}$
, which is trivial. Now suppose the claim holds for m. Then
from the instance
![]() ${(A_{1} \mathbin {\rightarrow } A_{m+1}) \lor (A_{m+1} \mathbin {\rightarrow } A_{1})}$
of
${(A_{1} \mathbin {\rightarrow } A_{m+1}) \lor (A_{m+1} \mathbin {\rightarrow } A_{1})}$
of
![]() ${\mathit {Lin}}$
. By induction hypothesis,
${\mathit {Lin}}$
. By induction hypothesis,
and the claim follows by
![]() $\mathbf {H}$
.⊣
$\mathbf {H}$
.⊣
Lemma 8.3. Suppose
![]() $\mathbf {L} \vdash B_{m}$
. If
$\mathbf {L} \vdash B_{m}$
. If
![]() $\Delta (e)$
are the impredicative critical formulas belonging to the
$\Delta (e)$
are the impredicative critical formulas belonging to the
![]() ${\varepsilon \tau }$
-term e, then
${\varepsilon \tau }$
-term e, then
![]() $\Delta (e)$
has an e-elimination set.
$\Delta (e)$
has an e-elimination set.
Proof. Suppose
![]() $\Gamma , \Delta (e), \Pi (e) \vdash _{\mathbf {L}} D(e)$
, where
$\Gamma , \Delta (e), \Pi (e) \vdash _{\mathbf {L}} D(e)$
, where
![]() $\Pi (e)$
is the set of predicative critical formulas belonging to e.
$\Pi (e)$
is the set of predicative critical formulas belonging to e.
Suppose
![]() $\Pi (e)$
and
$\Pi (e)$
and
![]() $\Delta (e)$
consist of, respectively, the critical formulas
$\Delta (e)$
consist of, respectively, the critical formulas
 $$ \begin{align*} C_{u_{i}}(e) & \equiv A(u_{i}) \mathbin{\rightarrow} A(e),\\ C_{s_{i}}(e) & \equiv A(s_{i}(e)) \mathbin{\rightarrow} A(e). \end{align*} $$
$$ \begin{align*} C_{u_{i}}(e) & \equiv A(u_{i}) \mathbin{\rightarrow} A(e),\\ C_{s_{i}}(e) & \equiv A(s_{i}(e)) \mathbin{\rightarrow} A(e). \end{align*} $$
The proof generalizes the preceding example: we successively substitute terms for e in such a way that a disjunction of instances of D is implied by substitution instances of the critical formulas in
![]() $\Gamma $
together with a disjunction of the form
$\Gamma $
together with a disjunction of the form
![]() ${B_{m}}$
plus the predicative critical formulas
${B_{m}}$
plus the predicative critical formulas
![]() $\Pi (e)$
. Once
$\Pi (e)$
. Once
![]() $k = m$
, the disjunction becomes provable from
$k = m$
, the disjunction becomes provable from
![]() ${B_{m}}$
.
${B_{m}}$
.
Let
![]() $T_{0} = \{e\}$
and
$T_{0} = \{e\}$
and
![]() $T_{i+1} = \{s_{j}(t) : t \in T_{i}, j \le r\}$
. Let
$T_{i+1} = \{s_{j}(t) : t \in T_{i}, j \le r\}$
. Let
![]() $\Gamma (T) = \{C[t/e] : C \in \Gamma , t \in T\}$
. If w is a word over
$\Gamma (T) = \{C[t/e] : C \in \Gamma , t \in T\}$
. If w is a word over
![]() $\{s_{1}, \dots , s_{r}\}$
, i.e.,
$\{s_{1}, \dots , s_{r}\}$
, i.e.,
![]() $w = s_{i_{1}}\dots s_{i_{k}}$
then we write
$w = s_{i_{1}}\dots s_{i_{k}}$
then we write
![]() $w_{j}(t)$
for
$w_{j}(t)$
for
![]() $s_{i_{j}}(s_{i_{j+1}}(\dots s_{i_{k}}(t)\dots ))$
. So, e.g., if
$s_{i_{j}}(s_{i_{j+1}}(\dots s_{i_{k}}(t)\dots ))$
. So, e.g., if
![]() $w=sst$
then
$w=sst$
then
![]() $w_{1}(e)$
is
$w_{1}(e)$
is
![]() $s(s(t(e)))$
,
$s(s(t(e)))$
,
![]() $w_{3}(e) = t(e)$
, and
$w_{3}(e) = t(e)$
, and
![]() $w_{4}(e) = e$
. Let
$w_{4}(e) = e$
. Let
![]() $W(m)$
be the set of all length m words over
$W(m)$
be the set of all length m words over
![]() $s_{1}$
, …,
$s_{1}$
, …,
![]() $s_{r}$
.
$s_{r}$
.
We show by induction on m that
 $$ \begin{align*} \Gamma, \Gamma(T_{1}), \dots, \Gamma(T_{m-1}), \Lambda_{m}, \Pi(e) & \vdash_{\mathbf{L}} \bigvee_{i=1}^{m} \bigvee_{t\in T_{i-1}} D(t), \end{align*} $$
$$ \begin{align*} \Gamma, \Gamma(T_{1}), \dots, \Gamma(T_{m-1}), \Lambda_{m}, \Pi(e) & \vdash_{\mathbf{L}} \bigvee_{i=1}^{m} \bigvee_{t\in T_{i-1}} D(t), \end{align*} $$
where
 $$ \begin{align*} \Lambda_{i} & = \left\{ \bigvee_{i=1}^{m} C(w,i) : w \in W(m)\right\} \text{ and}\\ C(w,i) & \equiv A(w_{i}(e)) \mathbin{\rightarrow} A(w_{i+1}(e)). \end{align*} $$
$$ \begin{align*} \Lambda_{i} & = \left\{ \bigvee_{i=1}^{m} C(w,i) : w \in W(m)\right\} \text{ and}\\ C(w,i) & \equiv A(w_{i}(e)) \mathbin{\rightarrow} A(w_{i+1}(e)). \end{align*} $$
The induction basis is
![]() $m=1$
. Then
$m=1$
. Then
 $$ \begin{align*} T_{1} & = \{s_{1}(e), \dots, s_{r}(e)\},\\ W(1) & = \{s_{1}, \dots, s_{r}\},\\ C(s_{j},1) & \equiv A(s_{j}(e)) \mathbin{\rightarrow} A(e), \end{align*} $$
$$ \begin{align*} T_{1} & = \{s_{1}(e), \dots, s_{r}(e)\},\\ W(1) & = \{s_{1}, \dots, s_{r}\},\\ C(s_{j},1) & \equiv A(s_{j}(e)) \mathbin{\rightarrow} A(e), \end{align*} $$
and so each disjunction in
![]() $\Lambda _{i}$
is just one of the impredicative critical formulas
$\Lambda _{i}$
is just one of the impredicative critical formulas
![]() $A(s_{j}(e)) \mathbin {\rightarrow } A(e))$
, i.e.,
$A(s_{j}(e)) \mathbin {\rightarrow } A(e))$
, i.e.,
![]() $\Lambda _{1} = \Delta (e)$
. Likewise, the disjunction on the right is just
$\Lambda _{1} = \Delta (e)$
. Likewise, the disjunction on the right is just
![]() $D(e)$
. So the claim holds by the assumption that
$D(e)$
. So the claim holds by the assumption that
![]() $\Gamma , \Delta (e), \Pi (e) \vdash D(e)$
.
$\Gamma , \Delta (e), \Pi (e) \vdash D(e)$
.
Now let
![]() $v = s_{i_{1}}\dots s_{i_{m}}$
be a length m word, and
$v = s_{i_{1}}\dots s_{i_{m}}$
be a length m word, and
 $$ \begin{align*} \Lambda_{m}(v) & = \left\{ \bigvee_{i=1}^{m} (A(w_{i}(e)) \mathbin{\rightarrow} A(w_{i+1}(e)) : w \in W(m) \setminus \{v\}\right\},\\ C(v) & \equiv \bigvee_{i=1}^{m} (A(v_{i}(e)) \mathbin{\rightarrow} A(v_{i+1}(e)). \end{align*} $$
$$ \begin{align*} \Lambda_{m}(v) & = \left\{ \bigvee_{i=1}^{m} (A(w_{i}(e)) \mathbin{\rightarrow} A(w_{i+1}(e)) : w \in W(m) \setminus \{v\}\right\},\\ C(v) & \equiv \bigvee_{i=1}^{m} (A(v_{i}(e)) \mathbin{\rightarrow} A(v_{i+1}(e)). \end{align*} $$
In other words,
![]() $\Lambda _{m} = \Lambda _{m}(v) \cup \{C(v)\}$
. We’ll abbreviate
$\Lambda _{m} = \Lambda _{m}(v) \cup \{C(v)\}$
. We’ll abbreviate
![]() $\Gamma (T_{1})$
, …,
$\Gamma (T_{1})$
, …,
![]() $\Gamma (T_{m-1})$
as
$\Gamma (T_{m-1})$
as
![]() $\Gamma ^{\prime }$
, and
$\Gamma ^{\prime }$
, and
![]() $\bigvee _{i=1}^{m} \bigvee _{t\in T_{i-1}} D(t)$
as
$\bigvee _{i=1}^{m} \bigvee _{t\in T_{i-1}} D(t)$
as
![]() $D^{\prime }$
. The induction hypothesis can then be written as:
$D^{\prime }$
. The induction hypothesis can then be written as:
Take
![]() $t = v_{1}(e)$
, i.e.,
$t = v_{1}(e)$
, i.e.,
![]() $s_{i_{1}}(\dots s_{i_{m}}(e))$
. By replacing e by t in
$s_{i_{1}}(\dots s_{i_{m}}(e))$
. By replacing e by t in
![]() $\pi $
, we have
$\pi $
, we have
 $$ \begin{align*} \Gamma(t), \Lambda(t), \Pi(t) & \vdash_{\mathbf{L}} D(t) \text{ and so also}\\ \Gamma(t), \bigwedge \Lambda(t) \land \bigwedge \Pi(t) & \vdash_{\mathbf{L}} D(t). \end{align*} $$
$$ \begin{align*} \Gamma(t), \Lambda(t), \Pi(t) & \vdash_{\mathbf{L}} D(t) \text{ and so also}\\ \Gamma(t), \bigwedge \Lambda(t) \land \bigwedge \Pi(t) & \vdash_{\mathbf{L}} D(t). \end{align*} $$
Combining this with the induction hypothesis using Lemma 7.5(1) we have
 $$ \begin{align*} \Gamma, \Gamma^{\prime}, \Gamma(t), &\\ \left(\bigwedge \Lambda(t) \land \bigwedge \Pi(t)\right) \lor C(v), &\\ \Lambda_{m}(v), \Pi(e) & \vdash_{\mathbf{L}} D^{\prime} \lor D(t). \end{align*} $$
$$ \begin{align*} \Gamma, \Gamma^{\prime}, \Gamma(t), &\\ \left(\bigwedge \Lambda(t) \land \bigwedge \Pi(t)\right) \lor C(v), &\\ \Lambda_{m}(v), \Pi(e) & \vdash_{\mathbf{L}} D^{\prime} \lor D(t). \end{align*} $$
If we write
![]() ${\Xi \lor G}$
for
${\Xi \lor G}$
for
![]() $\{F \lor G : F \in \Xi \}$
, by distributivity,
$\{F \lor G : F \in \Xi \}$
, by distributivity,
 $$ \begin{align*} \Gamma, \Gamma^{\prime}, \Gamma(t),&\\ \Lambda(t) \lor C(v),&\\ \Pi(t) \lor C(v),&\\ \Lambda_{m}(v), \Pi(e) & \vdash_{\mathbf{L}} D^{\prime} \lor D(t). \end{align*} $$
$$ \begin{align*} \Gamma, \Gamma^{\prime}, \Gamma(t),&\\ \Lambda(t) \lor C(v),&\\ \Pi(t) \lor C(v),&\\ \Lambda_{m}(v), \Pi(e) & \vdash_{\mathbf{L}} D^{\prime} \lor D(t). \end{align*} $$
Recall that
![]() $t \equiv v_{1}(e)$
where v is a word of length m. The formulas in
$t \equiv v_{1}(e)$
where v is a word of length m. The formulas in
![]() $\Pi (t)$
are of the form
$\Pi (t)$
are of the form
![]() $A(u_{i}) \mathbin {\rightarrow } A(v_{1}(e))$
, so a formula in
$A(u_{i}) \mathbin {\rightarrow } A(v_{1}(e))$
, so a formula in
![]() $\Pi (t) \lor C(v)$
is of the form
$\Pi (t) \lor C(v)$
is of the form
Every such formula is implied by
![]() $A(u_{i}) \mathbin {\rightarrow } A(e)$
by Lemma 8.2, since
$A(u_{i}) \mathbin {\rightarrow } A(e)$
by Lemma 8.2, since
![]() $\mathbf {H} + {B_{m}} \vdash \mathit {Lin}$
by Proposition 6.4. Since
$\mathbf {H} + {B_{m}} \vdash \mathit {Lin}$
by Proposition 6.4. Since
![]() $A(u_{i}) \mathbin {\rightarrow } A(e)$
is in
$A(u_{i}) \mathbin {\rightarrow } A(e)$
is in
![]() $\Pi (e)$
, we get:
$\Pi (e)$
, we get:
Every formula in
![]() $\Lambda (t) \lor C(v)$
is of the form
$\Lambda (t) \lor C(v)$
is of the form
![]() ${B_{m}}$
, specifically,
${B_{m}}$
, specifically,
Since for each
![]() $i \le r$
,
$i \le r$
,
![]() $A(s_{i}(v_{1}(e))) \mathbin {\rightarrow } A(v_{1}(e)) \in \Lambda (t)$
,
$A(s_{i}(v_{1}(e))) \mathbin {\rightarrow } A(v_{1}(e)) \in \Lambda (t)$
,
![]() $\Lambda (t) \lor C(v)$
is the set of all disjunctions
$\Lambda (t) \lor C(v)$
is the set of all disjunctions
 $$ \begin{align*} \bigvee_{i=1}^{m+1} (A(w_{i}(e)) \mathbin{\rightarrow} A(w_{i+1}(e))), \end{align*} $$
$$ \begin{align*} \bigvee_{i=1}^{m+1} (A(w_{i}(e)) \mathbin{\rightarrow} A(w_{i+1}(e))), \end{align*} $$
where
![]() $w = s_{i}v$
for some
$w = s_{i}v$
for some
![]() $i \le r$
. As every length
$i \le r$
. As every length
![]() $m+1$
word is of this form for some length m word v, repeating this process for all length m words v thus yields
$m+1$
word is of this form for some length m word v, repeating this process for all length m words v thus yields
As we’ve seen, a formula in
![]() $\Lambda _{m}$
is of the form
$\Lambda _{m}$
is of the form
![]() ${B_{m}}$
, so in
${B_{m}}$
, so in
![]() $\mathbf {L} + {B_{m}}$
, we have
$\mathbf {L} + {B_{m}}$
, we have
 $$ \begin{align*} \Gamma, \Gamma(T_{1}), \dots, \Gamma(T_{m-1}), \Pi(e) & \vdash_{\mathbf{L}} \bigvee_{i=1}^{m} \bigvee_{t\in T_{i-1}} D(t). \end{align*} $$
$$ \begin{align*} \Gamma, \Gamma(T_{1}), \dots, \Gamma(T_{m-1}), \Pi(e) & \vdash_{\mathbf{L}} \bigvee_{i=1}^{m} \bigvee_{t\in T_{i-1}} D(t). \end{align*} $$
Thus, the claim follows by taking
![]() $T = \{e\} \cup T_{m-1}$
.
$T = \{e\} \cup T_{m-1}$
.
If e is a
![]() $\tau $
-term, the proof proceeds analogously. The resulting formulas in
$\tau $
-term, the proof proceeds analogously. The resulting formulas in
![]() $\Lambda (e)$
are then of the form
$\Lambda (e)$
are then of the form
![]() $(A_{m} \mathbin {\rightarrow } A_{m+1}) \lor \dots \lor (A_{1} \mathbin {\rightarrow } A_{2})$
which is equivalent to
$(A_{m} \mathbin {\rightarrow } A_{m+1}) \lor \dots \lor (A_{1} \mathbin {\rightarrow } A_{2})$
which is equivalent to
![]() ${B_{m}}$
.⊣
${B_{m}}$
.⊣
Lemma 8.4. If
![]() $\mathbf {L} \vdash \mathit {Lin}$
,
$\mathbf {L} \vdash \mathit {Lin}$
,
-
1.
 $\mathbf {L} \vdash \bigvee _{j=1}^{m} \bigwedge _{i=1}^{m} (A_{i} \mathbin {\rightarrow } A_{j}),$
$\mathbf {L} \vdash \bigvee _{j=1}^{m} \bigwedge _{i=1}^{m} (A_{i} \mathbin {\rightarrow } A_{j}),$
-
2.
 $\mathbf {L} \vdash \bigvee _{j=1}^{m} \bigwedge _{i=1}^{m} (A_{j} \mathbin {\rightarrow } A_{i}).$
$\mathbf {L} \vdash \bigvee _{j=1}^{m} \bigwedge _{i=1}^{m} (A_{j} \mathbin {\rightarrow } A_{i}).$
Proof. As propositional infinite-valued Gödel logic
![]() $\mathbf {G}_{\mathbb {R}}$
is axiomatized by
$\mathbf {G}_{\mathbb {R}}$
is axiomatized by
![]() $\mathbf {H} + \mathit {Lin}$
, it suffices to show that the formulas are valid in the Gödel logic based on the truth value set
$\mathbf {H} + \mathit {Lin}$
, it suffices to show that the formulas are valid in the Gödel logic based on the truth value set
![]() $[0,1]$
. For (1), in any given valuation, one of the
$[0,1]$
. For (1), in any given valuation, one of the
![]() $A_{j}$
must be maximal, i.e.,
$A_{j}$
must be maximal, i.e.,
![]() $A_{i} \mathbin {\rightarrow } A_{j}$
has value
$A_{i} \mathbin {\rightarrow } A_{j}$
has value
![]() $1$
in it for all i. For (2), one of the
$1$
in it for all i. For (2), one of the
![]() $A_{j}$
must be minimal.⊣
$A_{j}$
must be minimal.⊣
Lemma 8.5. Suppose
![]() $\mathbf {L} \vdash \mathit {Lin}$
and
$\mathbf {L} \vdash \mathit {Lin}$
and
![]() $\Gamma , \Pi (e) \vdash _{\mathbf {L}} D(e)$
, where
$\Gamma , \Pi (e) \vdash _{\mathbf {L}} D(e)$
, where
![]() $\Pi (e)$
are the predicative critical formulas
$\Pi (e)$
are the predicative critical formulas
![]() $A(u_{j}) \mathbin {\rightarrow } A(e)$
belonging to e, there are no impredicative critical formulas belonging to e, and
$A(u_{j}) \mathbin {\rightarrow } A(e)$
belonging to e, there are no impredicative critical formulas belonging to e, and
![]() $\Gamma $
are critical formulas for which e is not critical. Then
$\Gamma $
are critical formulas for which e is not critical. Then
![]() $\Pi (e)$
has a complete e-elimination set.
$\Pi (e)$
has a complete e-elimination set.
Proof. First suppose e is an
![]() $\varepsilon $
-term. Replacing e by
$\varepsilon $
-term. Replacing e by
![]() $u_{j}$
results in a proof showing
$u_{j}$
results in a proof showing
 $$ \begin{align*} \Gamma[u_{j}/e], \bigwedge_{i=1}^{p} (A(u_{i}) \mathbin{\rightarrow} A(u_{j})) & \vdash_{\mathbf{L}} D(u_{j}). \end{align*} $$
$$ \begin{align*} \Gamma[u_{j}/e], \bigwedge_{i=1}^{p} (A(u_{i}) \mathbin{\rightarrow} A(u_{j})) & \vdash_{\mathbf{L}} D(u_{j}). \end{align*} $$
By applying Lemma 7.5(1), we get
 $$ \begin{align*} \bigcup_{j} \Gamma[u_{j}/e], \bigvee_{j=1}^{p} \bigwedge_{i=1}^{p} (A(u_{i}) \mathbin{\rightarrow} A(u_{j})) & \vdash_{\mathbf{L}} \bigvee_{j} D(u_{j}). \end{align*} $$
$$ \begin{align*} \bigcup_{j} \Gamma[u_{j}/e], \bigvee_{j=1}^{p} \bigwedge_{i=1}^{p} (A(u_{i}) \mathbin{\rightarrow} A(u_{j})) & \vdash_{\mathbf{L}} \bigvee_{j} D(u_{j}). \end{align*} $$
The disjunction of conjunctions on the left is provable in
![]() $\mathbf {L} + \mathit {Lin}$
by Lemma 8.4(1).
$\mathbf {L} + \mathit {Lin}$
by Lemma 8.4(1).
If e is a
![]() $\tau $
-term, we get
$\tau $
-term, we get
 $$ \begin{align*} \bigcup_{j} \Gamma[u_{j}/e], \bigvee_{j=1}^{p} \bigwedge_{i=1}^{p} (A(u_{j}) \mathbin{\rightarrow} A(u_{i})) \vdash_{\mathbf{L}} \bigvee_{j} D(u_{j}), \end{align*} $$
$$ \begin{align*} \bigcup_{j} \Gamma[u_{j}/e], \bigvee_{j=1}^{p} \bigwedge_{i=1}^{p} (A(u_{j}) \mathbin{\rightarrow} A(u_{i})) \vdash_{\mathbf{L}} \bigvee_{j} D(u_{j}), \end{align*} $$
and the claim follows by Lemma 8.4(2).⊣
Theorem 8.6. If
![]() $\mathbf {L} \vdash {B_{m}}$
for some m, then
$\mathbf {L} \vdash {B_{m}}$
for some m, then
![]() $\mathbf {L}{\varepsilon \tau }$
has complete e-elimination sets.
$\mathbf {L}{\varepsilon \tau }$
has complete e-elimination sets.
Proof. Suppose
![]() $\Gamma , \Pi (e), \Delta (e) \vdash _{\mathbf {L}} D(e)$
, where
$\Gamma , \Pi (e), \Delta (e) \vdash _{\mathbf {L}} D(e)$
, where
![]() $\Pi (e)$
are the predicative critical formulas belonging to e,
$\Pi (e)$
are the predicative critical formulas belonging to e,
![]() $\Delta (e)$
the impredicative formulas belonging to e, and
$\Delta (e)$
the impredicative formulas belonging to e, and
![]() $\Gamma $
are critical formulas for which e is not critical. By Lemma 8.3,
$\Gamma $
are critical formulas for which e is not critical. By Lemma 8.3,
![]() $\Gamma [T], \Pi (e) \vdash _{\mathbf {L}} \bigvee _{t\in T} D(t)$
where
$\Gamma [T], \Pi (e) \vdash _{\mathbf {L}} \bigvee _{t\in T} D(t)$
where
![]() $T = \{e\} \cup T_{m-1}$
. Since
$T = \{e\} \cup T_{m-1}$
. Since
![]() $\mathbf {L}+{B_{m}} \vdash \mathit {Lin}$
by Proposition 6.4, Lemma 8.5 applies and so
$\mathbf {L}+{B_{m}} \vdash \mathit {Lin}$
by Proposition 6.4, Lemma 8.5 applies and so
![]() $\bigcup _{j} T[u_{j}/e]$
is a complete e-elimination set.⊣
$\bigcup _{j} T[u_{j}/e]$
is a complete e-elimination set.⊣
Remark 8.7. The proof of Proposition 7.7 provides essentially Hilbert’s way of computing e-elimination sets using excluded middle. However, instead of excluded middle
![]() $A \lor \lnot A$
, classical logic can also be axiomatized over
$A \lor \lnot A$
, classical logic can also be axiomatized over
![]() $\mathbf {H}{}$
by
$\mathbf {H}{}$
by
![]() ${B_{2}}$
, i.e.,
${B_{2}}$
, i.e.,
![]() $(A \mathbin {\rightarrow } B) \lor (B \mathbin {\rightarrow } C)$
. The method of computing e-elimination sets using Lemmas 8.3 and 8.5 applied to
$(A \mathbin {\rightarrow } B) \lor (B \mathbin {\rightarrow } C)$
. The method of computing e-elimination sets using Lemmas 8.3 and 8.5 applied to
![]() $\mathbf {LC}_{2} = \mathbf {C}$
provides a method for computing e-elimination sets (and hence of Herbrand disjunctions) different from Hilbert’s method.
$\mathbf {LC}_{2} = \mathbf {C}$
provides a method for computing e-elimination sets (and hence of Herbrand disjunctions) different from Hilbert’s method.
9 The Hilbert–Bernays elimination procedure
Recall that the challenges in the proof of the extended first
![]() ${\varepsilon \tau }$
-theorem include, in addition to the existence of complete elimination sets, guarantees that the new sets
${\varepsilon \tau }$
-theorem include, in addition to the existence of complete elimination sets, guarantees that the new sets
![]() $\Gamma [s_{i}/e]$
are in fact critical formulas (so eliminating a set
$\Gamma [s_{i}/e]$
are in fact critical formulas (so eliminating a set
![]() $\Lambda (e)$
of critical formulas yields a correct
$\Lambda (e)$
of critical formulas yields a correct
![]() $\mathbf {L}{\varepsilon \tau }$
-proof), and that the process eventually terminates. In Hilbert and Bernays’s original proof of the first
$\mathbf {L}{\varepsilon \tau }$
-proof), and that the process eventually terminates. In Hilbert and Bernays’s original proof of the first
![]() $\varepsilon $
-theorem, this was ensured by processing sets of critical formulas in a specific order. We briefly review this proof, concentrating on its structure, since we’ll apply the same method to critical formulas in
$\varepsilon $
-theorem, this was ensured by processing sets of critical formulas in a specific order. We briefly review this proof, concentrating on its structure, since we’ll apply the same method to critical formulas in
![]() ${\varepsilon \tau }$
-proofs for intermediate logics.
${\varepsilon \tau }$
-proofs for intermediate logics.
Definition 9.1. Suppose
![]() $\vdash _{\mathbf {L}{\varepsilon \tau }}^{\pi _{1}} D_{1}$
. A sequence
$\vdash _{\mathbf {L}{\varepsilon \tau }}^{\pi _{1}} D_{1}$
. A sequence
![]() $\langle \Lambda _{1}(e_{1}),T_{1}\rangle $
, …,
$\langle \Lambda _{1}(e_{1}),T_{1}\rangle $
, …,
![]() $\langle \Lambda _{k}(e_{k}),T_{k}\rangle $
is an
$\langle \Lambda _{k}(e_{k}),T_{k}\rangle $
is an
![]() ${\varepsilon \tau }$
-elimination sequence iff, for each i,
${\varepsilon \tau }$
-elimination sequence iff, for each i,
-
1.
 $\Lambda _{i}(e_{i})$
is a set of critical formulas belonging to
$\Lambda _{i}(e_{i})$
is a set of critical formulas belonging to
 $e_{i}$
,
$e_{i}$
, -
2.
 $\Gamma _{i}, \Lambda ^{\prime }(e), \Lambda _{i}(e_{i}) \vdash _{\mathbf {L}{\varepsilon \tau }}^{\pi _{i}} D_{i}$
, where
$\Gamma _{i}, \Lambda ^{\prime }(e), \Lambda _{i}(e_{i}) \vdash _{\mathbf {L}{\varepsilon \tau }}^{\pi _{i}} D_{i}$
, where
 $\Lambda ^{\prime }(e)$
are the critical formulas for
$\Lambda ^{\prime }(e)$
are the critical formulas for
 $e_{i}$
not in
$e_{i}$
not in
 $\Lambda _{i}(e_{i})$
, and
$\Lambda _{i}(e_{i})$
, and
 $\Gamma _{i}$
the remaining critical formulas in
$\Gamma _{i}$
the remaining critical formulas in
 $\pi _{i}$
,
$\pi _{i}$
, -
3.
 $T_{i}$
is an
$T_{i}$
is an
 $e_{i}$
-elimination set for
$e_{i}$
-elimination set for
 $\pi _{i}$
and
$\pi _{i}$
and
 $\Lambda _{i}(e_{i})$
,
$\Lambda _{i}(e_{i})$
, -
4.
 $\Gamma _{i+1} = \Gamma _{i}[T_{i}/e_{i}]$
and
$\Gamma _{i+1} = \Gamma _{i}[T_{i}/e_{i}]$
and
 $D_{i+1} = \bigvee _{t\in T_{i}} D_{i}[t/e_{i}]$
,
$D_{i+1} = \bigvee _{t\in T_{i}} D_{i}[t/e_{i}]$
, -
5.
 $\Gamma _{i+1} \vdash _{\mathbf {L}{\varepsilon \tau }} D_{i+1}$
,
$\Gamma _{i+1} \vdash _{\mathbf {L}{\varepsilon \tau }} D_{i+1}$
,
and
![]() $\Gamma _{k+1} = \emptyset $
, that is,
$\Gamma _{k+1} = \emptyset $
, that is,
![]() $\mathbf {L} \vdash ^{\pi _{k+1}} D_{k+1}$
. If all
$\mathbf {L} \vdash ^{\pi _{k+1}} D_{k+1}$
. If all
![]() $\Lambda ^{\prime }(e_{i}) = \emptyset $
(i.e.,
$\Lambda ^{\prime }(e_{i}) = \emptyset $
(i.e.,
![]() $T_{i}$
is a complete elimination set for
$T_{i}$
is a complete elimination set for
![]() $e_{i}$
), we say the sequence is a complete elimination sequence.
$e_{i}$
), we say the sequence is a complete elimination sequence.
An
![]() ${\varepsilon \tau }$
-elimination sequence is a sequence of
${\varepsilon \tau }$
-elimination sequence is a sequence of
![]() ${\varepsilon \tau }$
-terms
${\varepsilon \tau }$
-terms
![]() $e_{i}$
and sets of critical formulas
$e_{i}$
and sets of critical formulas
![]() $\Lambda (e_{i})$
belonging to it, such that eliminating
$\Lambda (e_{i})$
belonging to it, such that eliminating
![]() $\Lambda _{i}(e_{i})$
from proof
$\Lambda _{i}(e_{i})$
from proof
![]() $\pi _{i}$
results in a new proof
$\pi _{i}$
results in a new proof
![]() $\pi _{i+1}$
of a disjunction of instances of
$\pi _{i+1}$
of a disjunction of instances of
![]() $D(e_{i})$
. This new proof proceeds from instances of the critical formulas for which
$D(e_{i})$
. This new proof proceeds from instances of the critical formulas for which
![]() $e_{i}$
is not critical and the remaining critical formulas belonging to
$e_{i}$
is not critical and the remaining critical formulas belonging to
![]() $e_{i}$
. Since the definition requires
$e_{i}$
. Since the definition requires
![]() $\pi _{i}$
to be an
$\pi _{i}$
to be an
![]() ${\varepsilon \tau }$
-proof, the formulas in
${\varepsilon \tau }$
-proof, the formulas in
![]() $\Gamma [T_{i}]$
must actually be critical formulas.
$\Gamma [T_{i}]$
must actually be critical formulas.
If an
![]() ${\varepsilon \tau }$
-elimination sequence exists for a formula E and its
${\varepsilon \tau }$
-elimination sequence exists for a formula E and its
![]() ${\varepsilon \tau }$
-proof
${\varepsilon \tau }$
-proof
![]() $\pi _{0}$
, then the extended first
$\pi _{0}$
, then the extended first
![]() ${\varepsilon \tau }$
-theorem holds for E:
${\varepsilon \tau }$
-theorem holds for E:
Proposition 9.2. Suppose
![]() $\pi $
is an
$\pi $
is an
![]() $\mathbf {L}{\varepsilon \tau }$
proof of
$\mathbf {L}{\varepsilon \tau }$
proof of
![]() $E(u_{1}, \dots , u_{n})$
where
$E(u_{1}, \dots , u_{n})$
where
![]() $E(x_{1}, \dots , x_{n})$
is
$E(x_{1}, \dots , x_{n})$
is
![]() ${\varepsilon \tau }$
-free. Suppose furthermore that an
${\varepsilon \tau }$
-free. Suppose furthermore that an
![]() ${\varepsilon \tau }$
-elimination sequence exists for
${\varepsilon \tau }$
-elimination sequence exists for
![]() $\pi $
. Then there are tuples of terms
$\pi $
. Then there are tuples of terms
![]() $t_{i1}$
, …,
$t_{i1}$
, …,
![]() $t_{in}$
such that
$t_{in}$
such that
![]() $\mathbf {L} \vdash \bigvee _{i=1}^{l} E(t_{i1}, \dots , t_{in})$
.
$\mathbf {L} \vdash \bigvee _{i=1}^{l} E(t_{i1}, \dots , t_{in})$
.
Proof. Since
![]() $E(x_{1}, \dots , x_{n})$
is
$E(x_{1}, \dots , x_{n})$
is
![]() ${\varepsilon \tau }$
-free,
${\varepsilon \tau }$
-free,
![]() $E(t_{i1}, \dots , t_{in})[s/e] \equiv E(t_{i1}[s/e], \dots , t_{in}[s/e])$
. The result follows by induction on k, the length of the
$E(t_{i1}, \dots , t_{in})[s/e] \equiv E(t_{i1}[s/e], \dots , t_{in}[s/e])$
. The result follows by induction on k, the length of the
![]() ${\varepsilon \tau }$
-elimination sequence for
${\varepsilon \tau }$
-elimination sequence for
![]() $\pi $
.⊣
$\pi $
.⊣
For the proof of the extended first
![]() ${\varepsilon \tau }$
-theorem, then, it is sufficient to show that suitable e-elimination sets always exist, and that
${\varepsilon \tau }$
-theorem, then, it is sufficient to show that suitable e-elimination sets always exist, and that
![]() ${\varepsilon \tau }$
-terms e and sets of associated critical formulas can be successively chosen in such a way as to yield an
${\varepsilon \tau }$
-terms e and sets of associated critical formulas can be successively chosen in such a way as to yield an
![]() ${\varepsilon \tau }$
-elimination sequence for
${\varepsilon \tau }$
-elimination sequence for
![]() $\pi _{1}$
. Hilbert and Bernays did this by defining a well-ordering of
$\pi _{1}$
. Hilbert and Bernays did this by defining a well-ordering of
![]() ${\varepsilon \tau }$
-terms with the property that eliminating maximal
${\varepsilon \tau }$
-terms with the property that eliminating maximal
![]() ${\varepsilon \tau }$
-terms according to this ordering guarantees that the
${\varepsilon \tau }$
-terms according to this ordering guarantees that the
![]() $\Gamma [T_{i}]$
are again critical formulas, and that in each step no critical
$\Gamma [T_{i}]$
are again critical formulas, and that in each step no critical
![]() ${\varepsilon \tau }$
-terms are newly introduced which are larger (in the ordering).
${\varepsilon \tau }$
-terms are newly introduced which are larger (in the ordering).
The ordering used is the lexicographic order on two complexity measures of
![]() ${\varepsilon \tau }$
-terms e. We say that e is nested in an
${\varepsilon \tau }$
-terms e. We say that e is nested in an
![]() ${\varepsilon \tau }$
-term
${\varepsilon \tau }$
-term
![]() $e^{\prime }$
if e is a proper subterm of e, i.e., if every occurrence of a variable which is free in e is also free in
$e^{\prime }$
if e is a proper subterm of e, i.e., if every occurrence of a variable which is free in e is also free in
![]() $e^{\prime }$
. An
$e^{\prime }$
. An
![]() ${\varepsilon \tau }$
-term e is subordinate to
${\varepsilon \tau }$
-term e is subordinate to
![]() $e^{\prime } \equiv \varepsilon _{x}\,A(x)$
or
$e^{\prime } \equiv \varepsilon _{x}\,A(x)$
or
![]() $\equiv \tau _{x}\,A(x)$
if e occurs in
$\equiv \tau _{x}\,A(x)$
if e occurs in
![]() $e^{\prime }$
and x is free in e. The degree
$e^{\prime }$
and x is free in e. The degree
![]() $\mathrm {deg}(e)$
of e is the maximal level of nesting of subterms of e; the rank
$\mathrm {deg}(e)$
of e is the maximal level of nesting of subterms of e; the rank
![]() $\mathrm {rk}(e)$
the maximal level of subordination. When C is a critical formula belonging to e, we let
$\mathrm {rk}(e)$
the maximal level of subordination. When C is a critical formula belonging to e, we let
![]() $\mathrm {deg}(C) = \mathrm {deg}(e)$
and
$\mathrm {deg}(C) = \mathrm {deg}(e)$
and
![]() $\mathrm {rk}(C) = \mathrm {rk}(e)$
.
$\mathrm {rk}(C) = \mathrm {rk}(e)$
.
The Hilbert–Bernays elimination order proceeds by always picking a critical formula of maximal degree among the critical formulas of maximal rank. Its success relies on the following two lemmas, which establish that (a) replacement of maximal
![]() ${\varepsilon \tau }$
-terms in a critical formula results in a critical formula, and (b) if new critical formulas are generated, they are of lower rank, or of the same rank but of lower degree.
${\varepsilon \tau }$
-terms in a critical formula results in a critical formula, and (b) if new critical formulas are generated, they are of lower rank, or of the same rank but of lower degree.
Lemma 9.3. Suppose e is an
![]() ${\varepsilon \tau }$
-term, t is any term, C is a critical formula for which e is not critical, and
${\varepsilon \tau }$
-term, t is any term, C is a critical formula for which e is not critical, and
![]() $\mathrm {rk}(C) \le \mathrm {rk}(e)$
. Then
$\mathrm {rk}(C) \le \mathrm {rk}(e)$
. Then
![]() $C[t/e]$
is also a critical formula.
$C[t/e]$
is also a critical formula.
Lemma 9.4. Suppose e is an
![]() ${\varepsilon \tau }$
-term, t is any term, C is a critical formula for which e is not critical,
${\varepsilon \tau }$
-term, t is any term, C is a critical formula for which e is not critical,
![]() $\mathrm {rk}(C) \le \mathrm {rk}(e)$
, and if
$\mathrm {rk}(C) \le \mathrm {rk}(e)$
, and if
![]() $\mathrm {rk}(C) = \mathrm {rk}(e)$
then
$\mathrm {rk}(C) = \mathrm {rk}(e)$
then
![]() $\mathrm {deg}(C) \le \mathrm {deg}(e)$
. Then
$\mathrm {deg}(C) \le \mathrm {deg}(e)$
. Then
![]() $\mathrm {rk}(C[t/e]) \le \mathrm {rk}(e)$
, and if
$\mathrm {rk}(C[t/e]) \le \mathrm {rk}(e)$
, and if
![]() $\mathrm {rk}(C[t/e]) = \mathrm {rk}(e)$
, then
$\mathrm {rk}(C[t/e]) = \mathrm {rk}(e)$
, then
![]() $\mathrm {deg}(C[t/e]) \le \mathrm {deg}(e)$
.
$\mathrm {deg}(C[t/e]) \le \mathrm {deg}(e)$
.
The proofs of the preceding lemmas are as in [Reference Hilbert and Bernays15]; see also [Reference Moser and Zach23, Section 5], [Reference Zach, Ghosh and Prasad30, Section 4.1].
Proposition 9.5. Suppose
![]() $\pi $
is an
$\pi $
is an
![]() $\mathbf {L}{\varepsilon \tau }$
proof of
$\mathbf {L}{\varepsilon \tau }$
proof of
![]() $E(u_{1}, \dots , u_{n})$
where
$E(u_{1}, \dots , u_{n})$
where
![]() $E(x_{1}, \dots , x_{n})$
is
$E(x_{1}, \dots , x_{n})$
is
![]() ${\varepsilon \tau }$
-free. Suppose furthermore that for every
${\varepsilon \tau }$
-free. Suppose furthermore that for every
![]() $\mathbf {L}{\varepsilon \tau }$
proof and critical
$\mathbf {L}{\varepsilon \tau }$
proof and critical
![]() ${\varepsilon \tau }$
-term e there is a complete e-elimination set. Then there is a complete
${\varepsilon \tau }$
-term e there is a complete e-elimination set. Then there is a complete
![]() ${\varepsilon \tau }$
-elimination sequence for
${\varepsilon \tau }$
-elimination sequence for
![]() $\pi $
.
$\pi $
.
Proof. Take
![]() $\pi _{0} = \pi $
. Suppose
$\pi _{0} = \pi $
. Suppose
![]() $\pi _{i}$
has been defined. Let
$\pi _{i}$
has been defined. Let
![]() $e_{i}$
be a critical
$e_{i}$
be a critical
![]() ${\varepsilon \tau }$
-term of
${\varepsilon \tau }$
-term of
![]() $\pi _{i}$
of maximal degree among the critical terms of maximal rank. Let
$\pi _{i}$
of maximal degree among the critical terms of maximal rank. Let
![]() $\Lambda _{i}(e_{i})$
be all critical formulas belonging to
$\Lambda _{i}(e_{i})$
be all critical formulas belonging to
![]() $e_{i}$
, and
$e_{i}$
, and
![]() $\Gamma _{i}$
the remaining critical formulas. We have
$\Gamma _{i}$
the remaining critical formulas. We have
By assumption, there is a complete e-elimination set
![]() ${T_{i}}$
for
${T_{i}}$
for
![]() ${\Lambda _{i}(e_{i})}$
and so we have
${\Lambda _{i}(e_{i})}$
and so we have
![]() ${\pi _{i+1}}$
showing that
${\pi _{i+1}}$
showing that
Each critical formula C in
![]() $\Gamma _{i}$
is not of higher rank than
$\Gamma _{i}$
is not of higher rank than
![]() $e_{i}$
, and if it is of equal rank it is not of higher degree. So by Lemma 9.3,
$e_{i}$
, and if it is of equal rank it is not of higher degree. So by Lemma 9.3,
![]() $C[t/e_{i}]$
is a critical formula. Hence
$C[t/e_{i}]$
is a critical formula. Hence
![]() $\pi _{i+1}$
is a correct
$\pi _{i+1}$
is a correct
![]() $\mathbf {L}{\varepsilon \tau }$
-proof. Let
$\mathbf {L}{\varepsilon \tau }$
-proof. Let
![]() $\Gamma _{i+1} = \Gamma _{i}[T_{i}]$
and
$\Gamma _{i+1} = \Gamma _{i}[T_{i}]$
and
![]() $D_{i+1} \equiv \bigvee _{t\in T_{i}} D_{i}[t/e_{i}]$
.
$D_{i+1} \equiv \bigvee _{t\in T_{i}} D_{i}[t/e_{i}]$
.
Eventually,
![]() $\Gamma _{i} = \emptyset $
, since in each step, by Lemma 9.4, the maximal rank of critical
$\Gamma _{i} = \emptyset $
, since in each step, by Lemma 9.4, the maximal rank of critical
![]() ${\varepsilon \tau }$
-terms in
${\varepsilon \tau }$
-terms in
![]() $\Gamma _{i}$
does not increase, the maximal degree of critical
$\Gamma _{i}$
does not increase, the maximal degree of critical
![]() ${\varepsilon \tau }$
-terms of maximal rank does not increase, and the number of critical
${\varepsilon \tau }$
-terms of maximal rank does not increase, and the number of critical
![]() ${\varepsilon \tau }$
-terms of maximal degree among those of maximal rank decreases.⊣
${\varepsilon \tau }$
-terms of maximal degree among those of maximal rank decreases.⊣
Corollary 9.6. The extended first
![]() ${\varepsilon \tau }$
-theorem holds for
${\varepsilon \tau }$
-theorem holds for
![]() $\mathbf {C}$
.
$\mathbf {C}$
.
Proof. By Proposition 7.7, every critical
![]() ${\varepsilon \tau }$
-term has complete elimination sets. So by Proposition 9.5, there always is an elimination sequence. The extended first
${\varepsilon \tau }$
-term has complete elimination sets. So by Proposition 9.5, there always is an elimination sequence. The extended first
![]() ${\varepsilon \tau }$
-theorem follows by Proposition 9.2.⊣
${\varepsilon \tau }$
-theorem follows by Proposition 9.2.⊣
Remark 9.7. The traditional procedure following the Hilbert–Bernays order, which eliminates all critical formulas belonging to a maximal
![]() ${\varepsilon \tau }$
-term together, is not the only possible procedure that guarantees termination. We pointed out in Remark 7.8 that using Proposition 7.6 for all critical formulas belonging to a single
${\varepsilon \tau }$
-term together, is not the only possible procedure that guarantees termination. We pointed out in Remark 7.8 that using Proposition 7.6 for all critical formulas belonging to a single
![]() ${\varepsilon \tau }$
-term results in a larger disjunction than Proposition 7.7. Despite this, the ability in the classical case to eliminate single critical formulas provides flexibility that can be exploited to produce smaller overall Herbrand disjunctions. As Theorem 3 of [Reference Baaz, Leitsch, Lolic, Artemov and Nerode5] shows there are sequences of
${\varepsilon \tau }$
-term results in a larger disjunction than Proposition 7.7. Despite this, the ability in the classical case to eliminate single critical formulas provides flexibility that can be exploited to produce smaller overall Herbrand disjunctions. As Theorem 3 of [Reference Baaz, Leitsch, Lolic, Artemov and Nerode5] shows there are sequences of
![]() ${\varepsilon \tau }$
-proofs where the original procedure produces Herbrand disjunctions that are non-elementarily larger than a more efficient elimination order.
${\varepsilon \tau }$
-proofs where the original procedure produces Herbrand disjunctions that are non-elementarily larger than a more efficient elimination order.
Theorem 9.8. The extended first
![]() ${\varepsilon \tau }$
-theorem holds for negated formulas in any
${\varepsilon \tau }$
-theorem holds for negated formulas in any
![]() $\mathbf {L}{\varepsilon \tau }$
such that
$\mathbf {L}{\varepsilon \tau }$
such that
![]() $\mathbf {L} \vdash J$
, e.g.,
$\mathbf {L} \vdash J$
, e.g.,
![]() $\mathbf {KC}{\varepsilon \tau }$
and
$\mathbf {KC}{\varepsilon \tau }$
and
![]() $\mathbf {LC}{\varepsilon \tau }$
.
$\mathbf {LC}{\varepsilon \tau }$
.
Proof.
![]() $\mathbf {L}$
has complete e-elimination sets for end-formulas that are disjunctions of negated formulas, by Proposition 7.9. Note that J, i.e.,
$\mathbf {L}$
has complete e-elimination sets for end-formulas that are disjunctions of negated formulas, by Proposition 7.9. Note that J, i.e.,
![]() $\lnot A \lor \lnot \lnot A$
, follows intuitionistically from
$\lnot A \lor \lnot \lnot A$
, follows intuitionistically from
![]() $(A \mathbin {\rightarrow } \lnot A) \lor (\lnot A \mathbin {\rightarrow } A)$
, which is an instance of
$(A \mathbin {\rightarrow } \lnot A) \lor (\lnot A \mathbin {\rightarrow } A)$
, which is an instance of
![]() $\mathit {Lin}$
. So
$\mathit {Lin}$
. So
![]() $\mathbf {LC} \vdash J$
.⊣
$\mathbf {LC} \vdash J$
.⊣
Theorem 9.9. The extended first
![]() ${\varepsilon \tau }$
-theorem holds for
${\varepsilon \tau }$
-theorem holds for
![]() $\mathbf {LC}_{m}{\varepsilon \tau }$
.
$\mathbf {LC}_{m}{\varepsilon \tau }$
.
Proof. By Theorem 8.6, every critical
![]() ${\varepsilon \tau }$
-term has complete elimination sets. The extended first
${\varepsilon \tau }$
-term has complete elimination sets. The extended first
![]() ${\varepsilon \tau }$
-theorem follows by Propositions 9.2 and 9.5.⊣
${\varepsilon \tau }$
-theorem follows by Propositions 9.2 and 9.5.⊣
Theorem 9.10. The first
![]() ${\varepsilon \tau }$
-theorem holds in
${\varepsilon \tau }$
-theorem holds in
![]() $\mathbf {LC}{\varepsilon \tau }$
, i.e., if
$\mathbf {LC}{\varepsilon \tau }$
, i.e., if
![]() $\mathbf {LC}{\varepsilon \tau } \vdash D$
for an
$\mathbf {LC}{\varepsilon \tau } \vdash D$
for an
![]() ${\varepsilon \tau }$
-free formula D, then
${\varepsilon \tau }$
-free formula D, then
![]() $\mathbf {LC} \vdash D$
.
$\mathbf {LC} \vdash D$
.
Proof. If
![]() $\mathbf {LC}{\varepsilon \tau } \vdash D$
then also
$\mathbf {LC}{\varepsilon \tau } \vdash D$
then also
![]() $\mathbf {LC}_{m}{\varepsilon \tau } \vdash D$
. Since D is
$\mathbf {LC}_{m}{\varepsilon \tau } \vdash D$
. Since D is
![]() ${\varepsilon \tau }$
-free,
${\varepsilon \tau }$
-free,
![]() $\mathbf {LC}_{m} \vdash D$
by Theorem 9.9. In general
$\mathbf {LC}_{m} \vdash D$
by Theorem 9.9. In general
![]() $\mathbf {LC} \vdash D$
iff
$\mathbf {LC} \vdash D$
iff
![]() $\mathbf {LC}_{m} \vdash D$
for all m, so the claim follows.⊣
$\mathbf {LC}_{m} \vdash D$
for all m, so the claim follows.⊣
We are indebted to the referee for the Journal for the following observation:
Proposition 9.11. The first
![]() ${\varepsilon \tau }$
-theorem holds for negated formulas in
${\varepsilon \tau }$
-theorem holds for negated formulas in
![]() $\mathbf {L}{\varepsilon \tau }$
for any intermediate logic
$\mathbf {L}{\varepsilon \tau }$
for any intermediate logic
![]() $\mathbf {L}$
, including
$\mathbf {L}$
, including
![]() $\mathbf {H}:$
if
$\mathbf {H}:$
if
![]() $\mathbf {L}{\varepsilon \tau } \vdash \lnot D$
for an
$\mathbf {L}{\varepsilon \tau } \vdash \lnot D$
for an
![]() ${\varepsilon \tau }$
-free formula D, then
${\varepsilon \tau }$
-free formula D, then
![]() $\mathbf {L} \vdash D$
.
$\mathbf {L} \vdash D$
.
Proof. If
![]() $\mathbf {L}{\varepsilon \tau } \vdash \lnot D$
then also
$\mathbf {L}{\varepsilon \tau } \vdash \lnot D$
then also
![]() $\mathbf {C}{\varepsilon \tau } \vdash \lnot D$
. By the first
$\mathbf {C}{\varepsilon \tau } \vdash \lnot D$
. By the first
![]() $\varepsilon $
-theorem for
$\varepsilon $
-theorem for
![]() $\mathbf {C}$
(Corollary 9.6),
$\mathbf {C}$
(Corollary 9.6),
![]() $\mathbf {C} \vdash \lnot D$
, and by Glivenko’s Theorem,
$\mathbf {C} \vdash \lnot D$
, and by Glivenko’s Theorem,
![]() $\mathbf {H} \vdash \lnot D$
.
$\mathbf {H} \vdash \lnot D$
.
10 Herbrand’s theorem and the second epsilon-theorem
The extended first
![]() ${\varepsilon \tau }$
-theorem implies Herbrand’s theorem for purely existential formulas. If
${\varepsilon \tau }$
-theorem implies Herbrand’s theorem for purely existential formulas. If
![]() $E \equiv \exists x_{1}\ldots \exists x_{n} E^{\prime }(x_{1}, \ldots , x_{n})$
is provable in predicate logic, then so is
$E \equiv \exists x_{1}\ldots \exists x_{n} E^{\prime }(x_{1}, \ldots , x_{n})$
is provable in predicate logic, then so is
![]() $E^{\varepsilon \tau } \equiv E^{\prime }(e_{1}, \ldots , e_{n})$
for some
$E^{\varepsilon \tau } \equiv E^{\prime }(e_{1}, \ldots , e_{n})$
for some
![]() $\varepsilon $
-terms
$\varepsilon $
-terms
![]() $e_{1}$
, …,
$e_{1}$
, …,
![]() $e_{n}$
. From the extended first
$e_{n}$
. From the extended first
![]() $\varepsilon $
-theorem we then obtain a proof in propositional logic of a Herbrand disjunction
$\varepsilon $
-theorem we then obtain a proof in propositional logic of a Herbrand disjunction
for some terms
![]() $t_{i}^{j}$
. In predicate logic, we may now successively introduce existential quantifiers to obtain the original formula E. This holds in any intermediate predicate logic in which the first
$t_{i}^{j}$
. In predicate logic, we may now successively introduce existential quantifiers to obtain the original formula E. This holds in any intermediate predicate logic in which the first
![]() ${\varepsilon \tau }$
-theorem holds, since the only principles used in the last step (proving E from its Herbrand disjunction) are
${\varepsilon \tau }$
-theorem holds, since the only principles used in the last step (proving E from its Herbrand disjunction) are
![]() $A(t) \mathbin {\rightarrow } \exists x \,A(x)$
and
$A(t) \mathbin {\rightarrow } \exists x \,A(x)$
and
![]() $\exists x(A(x) \lor B) \mathbin {\rightarrow } (\exists x\,A(x) \lor B)$
, (x not free in B) which already hold in intuitionistic logic. (Despite the failure of the extended first
$\exists x(A(x) \lor B) \mathbin {\rightarrow } (\exists x\,A(x) \lor B)$
, (x not free in B) which already hold in intuitionistic logic. (Despite the failure of the extended first
![]() ${\varepsilon \tau }$
-theorem in
${\varepsilon \tau }$
-theorem in
![]() $\mathbf {LC}{\varepsilon \tau }$
, the Herbrand theorem for existential formulas does hold in
$\mathbf {LC}{\varepsilon \tau }$
, the Herbrand theorem for existential formulas does hold in
![]() $\mathbf {Q}\mathbf {LC}$
; see [Reference Aschieri3]).
$\mathbf {Q}\mathbf {LC}$
; see [Reference Aschieri3]).
For classical predicate logic, the Herbrand theorem for existential formulas implies the Herbrand theorem for prenex formulas. If a prenex formula E has a proof in first-order logic, so does its (purely existential) Herbrand form
![]() $H(E) = \exists x_{1}\ldots \exists x_{n} E^{\prime }(x_{1}, \ldots , x_{n})$
. In classical predicate logic, we can obtain not just
$H(E) = \exists x_{1}\ldots \exists x_{n} E^{\prime }(x_{1}, \ldots , x_{n})$
. In classical predicate logic, we can obtain not just
![]() $H(E)$
from its Herbrand disjunction, but also the original prenex formula E. This requires that we introduce not just existential quantifiers, but also universal quantifiers. Consequently, we need not just the generalization rule
$H(E)$
from its Herbrand disjunction, but also the original prenex formula E. This requires that we introduce not just existential quantifiers, but also universal quantifiers. Consequently, we need not just the generalization rule
![]() $A(x) / \forall x\,A(x)$
but also a principle that allows us to shift universal quantifiers over disjunctions, viz.,
$A(x) / \forall x\,A(x)$
but also a principle that allows us to shift universal quantifiers over disjunctions, viz.,
This principle is not intuitionistically valid: it characterizes Kripke frames with constant domains. Since the implication
![]() $E \mathbin {\rightarrow } H(E)$
already holds in intuitionistic logic, any intermediate predicate logic in which
$E \mathbin {\rightarrow } H(E)$
already holds in intuitionistic logic, any intermediate predicate logic in which
![]() $\mathit {CD}$
holds and which has the extended first
$\mathit {CD}$
holds and which has the extended first
![]() $\varepsilon $
-theorem also has Herbrand’s theorem for prenex formulas:
$\varepsilon $
-theorem also has Herbrand’s theorem for prenex formulas:
Proposition 10.1. Suppose
![]() ${\mathbf {Q}\mathbf {L} + \mathit {Ax}}$
proves
${\mathbf {Q}\mathbf {L} + \mathit {Ax}}$
proves
![]() $\mathit {CD}$
and
$\mathit {CD}$
and
![]() $\mathbf {L}{\varepsilon \tau }$
has the extended first
$\mathbf {L}{\varepsilon \tau }$
has the extended first
![]() ${\varepsilon \tau }$
-theorem. Then
${\varepsilon \tau }$
-theorem. Then
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
has Herbrand’s theorem for prenex formulas.
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
has Herbrand’s theorem for prenex formulas.
Although the extended first
![]() $\varepsilon $
-theorem implies Herbrand’s theorem for prenex formulas if
$\varepsilon $
-theorem implies Herbrand’s theorem for prenex formulas if
![]() $\mathit {CD}$
is provable, the converse is not true. As we showed in Theorem 6.2, the extended first
$\mathit {CD}$
is provable, the converse is not true. As we showed in Theorem 6.2, the extended first
![]() ${\varepsilon \tau }$
-theorem holds for
${\varepsilon \tau }$
-theorem holds for
![]() $\mathbf {L}{\varepsilon \tau }$
only if
$\mathbf {L}{\varepsilon \tau }$
only if
![]() $\mathbf {L} \vdash {B_{m}}$
for some m. In particular, it does not hold for infinite-valued first-order Gödel logics
$\mathbf {L} \vdash {B_{m}}$
for some m. In particular, it does not hold for infinite-valued first-order Gödel logics
![]() $\mathbf {G}_{\mathbb {R}} = \mathbf {Q}\mathbf {LC} + \mathit {CD}$
. However, Herbrand’s theorem for prenex formulas does hold for
$\mathbf {G}_{\mathbb {R}} = \mathbf {Q}\mathbf {LC} + \mathit {CD}$
. However, Herbrand’s theorem for prenex formulas does hold for
![]() $\mathbf {G}_{\mathbb {R}}$
; see [Reference Baaz, Preining and Zach6, Theorem 5.7], [Reference Baaz, Preining and Zach7, Theorem 7.8]. (Incidentally, the Herbrand theorem for prenex formulas also holds in intuitionistic logic despite the invalidity of
$\mathbf {G}_{\mathbb {R}}$
; see [Reference Baaz, Preining and Zach6, Theorem 5.7], [Reference Baaz, Preining and Zach7, Theorem 7.8]. (Incidentally, the Herbrand theorem for prenex formulas also holds in intuitionistic logic despite the invalidity of
![]() $\mathit {CD}$
; see [Reference Bowen10]).
$\mathit {CD}$
; see [Reference Bowen10]).
In classical logic, the second
![]() $\varepsilon $
-theorem can be proved using the extended first
$\varepsilon $
-theorem can be proved using the extended first
![]() $\varepsilon $
-theorem as follows: Suppose
$\varepsilon $
-theorem as follows: Suppose
![]() $\mathbf {C}{\varepsilon \tau } \vdash A^{\varepsilon \tau }$
. Since A is equivalent to a prenex formula
$\mathbf {C}{\varepsilon \tau } \vdash A^{\varepsilon \tau }$
. Since A is equivalent to a prenex formula
![]() $A^{p}$
in classical logic, we have
$A^{p}$
in classical logic, we have
![]() $\mathbf {Q}\mathbf {C} \vdash A \mathbin {\rightarrow } A^{p}$
. Prenex formulas imply their Herbrand forms, i.e.,
$\mathbf {Q}\mathbf {C} \vdash A \mathbin {\rightarrow } A^{p}$
. Prenex formulas imply their Herbrand forms, i.e.,
![]() $\mathbf {Q}\mathbf {C} \vdash A^{p} \mathbin {\rightarrow } H(A^{p})$
. Together we have
$\mathbf {Q}\mathbf {C} \vdash A^{p} \mathbin {\rightarrow } H(A^{p})$
. Together we have
![]() $\mathbf {Q}\mathbf {C} \vdash A \mathbin {\rightarrow } H(A^{p})$
and by translating into the
$\mathbf {Q}\mathbf {C} \vdash A \mathbin {\rightarrow } H(A^{p})$
and by translating into the
![]() ${\varepsilon \tau }$
-calculus,
${\varepsilon \tau }$
-calculus,
![]() $\mathbf {C}{\varepsilon \tau } \vdash A^{\varepsilon \tau } \mathbin {\rightarrow } H(A^{p})^{\varepsilon \tau }$
, so
$\mathbf {C}{\varepsilon \tau } \vdash A^{\varepsilon \tau } \mathbin {\rightarrow } H(A^{p})^{\varepsilon \tau }$
, so
![]() $\mathbf {C}{\varepsilon \tau } \vdash H(A^{p})^{\varepsilon \tau }$
. By the extended first
$\mathbf {C}{\varepsilon \tau } \vdash H(A^{p})^{\varepsilon \tau }$
. By the extended first
![]() ${\varepsilon \tau }$
-theorem,
${\varepsilon \tau }$
-theorem,
![]() $H(A^{p})$
has a Herbrand disjunction, from which (in
$H(A^{p})$
has a Herbrand disjunction, from which (in
![]() $\mathbf {Q}\mathbf {C}$
) we can prove
$\mathbf {Q}\mathbf {C}$
) we can prove
![]() $A^{p}$
and hence A.
$A^{p}$
and hence A.
The steps that may fail in an intermediate predicate logic
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
, other than the extended first
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
, other than the extended first
![]() ${\varepsilon \tau }$
-theorem, are the provability of
${\varepsilon \tau }$
-theorem, are the provability of
![]() $A \mathbin {\leftrightarrow } A^{p}$
and proving
$A \mathbin {\leftrightarrow } A^{p}$
and proving
![]() $A^{p}$
from the Herbrand disjunction of
$A^{p}$
from the Herbrand disjunction of
![]() $H(A^{p})$
. These steps do work provided all quantifier shifts can be carried out (i.e., in addition to
$H(A^{p})$
. These steps do work provided all quantifier shifts can be carried out (i.e., in addition to
![]() $\mathit {CD}$
also the formulas
$\mathit {CD}$
also the formulas
![]() $Q_{\forall }$
and
$Q_{\forall }$
and
![]() $Q_{\exists }$
). Thus, if
$Q_{\exists }$
). Thus, if
![]() $\mathbf {L}{\varepsilon \tau }$
has the extended first
$\mathbf {L}{\varepsilon \tau }$
has the extended first
![]() ${\varepsilon \tau }$
-theorem, any intermediate predicate logic
${\varepsilon \tau }$
-theorem, any intermediate predicate logic
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
in which all quantifier shifts are provable also has the second
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
in which all quantifier shifts are provable also has the second
![]() ${\varepsilon \tau }$
-theorem:
${\varepsilon \tau }$
-theorem:
Proposition 10.2. Suppose
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
proves
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
proves
![]() $\mathit {CD}$
,
$\mathit {CD}$
,
![]() $Q_{\exists }$
, and
$Q_{\exists }$
, and
![]() $Q_{\forall }$
, and
$Q_{\forall }$
, and
![]() $\mathbf {L}{\varepsilon \tau }$
has the extended first
$\mathbf {L}{\varepsilon \tau }$
has the extended first
![]() ${\varepsilon \tau }$
-theorem. Then
${\varepsilon \tau }$
-theorem. Then
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}$
has the second
$\mathbf {Q}\mathbf {L} + \mathit {Ax}$
has the second
![]() ${\varepsilon \tau }$
-theorem, i.e., if
${\varepsilon \tau }$
-theorem, i.e., if
![]() $\mathbf {L}{\varepsilon \tau } \vdash A^{\varepsilon \tau }$
then
$\mathbf {L}{\varepsilon \tau } \vdash A^{\varepsilon \tau }$
then
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash A$
.
$\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash A$
.
Proof. Suppose
![]() $\mathbf {L}{\varepsilon \tau } \vdash A^{\varepsilon \tau }$
. The
$\mathbf {L}{\varepsilon \tau } \vdash A^{\varepsilon \tau }$
. The
![]() ${\varepsilon \tau }$
-calculus proves
${\varepsilon \tau }$
-calculus proves
![]() ${\varepsilon \tau }$
-translations of all quantifier shifts, so
${\varepsilon \tau }$
-translations of all quantifier shifts, so
![]() $\mathbf {L}{\varepsilon \tau } \vdash (A^{p})^{\varepsilon \tau }$
, and since
$\mathbf {L}{\varepsilon \tau } \vdash (A^{p})^{\varepsilon \tau }$
, and since
![]() $\mathbf {Q}\mathbf {H} \vdash A^{p} \mathbin {\rightarrow } H(A^{p})$
also
$\mathbf {Q}\mathbf {H} \vdash A^{p} \mathbin {\rightarrow } H(A^{p})$
also
![]() $\mathbf {L}{\varepsilon \tau } \vdash (H(A^{p}))^{\varepsilon \tau }$
. By the extended first
$\mathbf {L}{\varepsilon \tau } \vdash (H(A^{p}))^{\varepsilon \tau }$
. By the extended first
![]() ${\varepsilon \tau }$
-theorem for
${\varepsilon \tau }$
-theorem for
![]() $\mathbf {L}{\varepsilon \tau }$
, there is a Herbrand disjunction
$\mathbf {L}{\varepsilon \tau }$
, there is a Herbrand disjunction
![]() $A^{\prime }$
of
$A^{\prime }$
of
![]() $H(A^{p})$
so that
$H(A^{p})$
so that
![]() $\mathbf {L} \vdash A^{\prime }$
. Since
$\mathbf {L} \vdash A^{\prime }$
. Since
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash \mathit {CD}$
,
$\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash \mathit {CD}$
,
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash A^{p}$
. Since
$\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash A^{p}$
. Since
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash Q_{\exists }$
and
$\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash Q_{\exists }$
and
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash Q_{\forall }$
, also
$\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash Q_{\forall }$
, also
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash A^{p} \mathbin {\rightarrow } A$
, and so
$\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash A^{p} \mathbin {\rightarrow } A$
, and so
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash A$
.⊣
$\mathbf {Q}\mathbf {L}+\mathit {Ax} \vdash A$
.⊣
Infinite-valued first-order Gödel logic
![]() $\mathbf {G}_{\mathbb {R}} = \mathbf {Q}\mathbf {LC} + \mathit {CD}$
is an intermediate predicate logic which proves
$\mathbf {G}_{\mathbb {R}} = \mathbf {Q}\mathbf {LC} + \mathit {CD}$
is an intermediate predicate logic which proves
![]() $\mathit {CD}$
but not
$\mathit {CD}$
but not
![]() $Q_{\forall }$
or
$Q_{\forall }$
or
![]() $Q_{\exists }$
, and the extended first
$Q_{\exists }$
, and the extended first
![]() ${\varepsilon \tau }$
-theorem does not hold for
${\varepsilon \tau }$
-theorem does not hold for
![]() $\mathbf {LC}{\varepsilon \tau }$
. The logics of linear Kripke frames with m worlds (and varying domains) are
$\mathbf {LC}{\varepsilon \tau }$
. The logics of linear Kripke frames with m worlds (and varying domains) are
![]() $\mathbf {Q}\mathbf {LC}_{m}$
. But
$\mathbf {Q}\mathbf {LC}_{m}$
. But
![]() $\mathbf {Q}\mathbf {LC}_{m}$
does not prove
$\mathbf {Q}\mathbf {LC}_{m}$
does not prove
![]() $\mathit {CD}$
, so it also does not have the second
$\mathit {CD}$
, so it also does not have the second
![]() ${\varepsilon \tau }$
-theorem:
${\varepsilon \tau }$
-theorem:
Proposition 10.3.
![]() $\mathbf {G}_{\mathbb {R}} = \mathbf {Q}\mathbf {LC} + \mathit {CD}$
and
$\mathbf {G}_{\mathbb {R}} = \mathbf {Q}\mathbf {LC} + \mathit {CD}$
and
![]() $\mathbf {Q}\mathbf {LC}_{m}$
do not have the second
$\mathbf {Q}\mathbf {LC}_{m}$
do not have the second
![]() ${\varepsilon \tau }$
-theorem.
${\varepsilon \tau }$
-theorem.
Proof. We have
![]() $\mathbf {LC}{\varepsilon \tau } \vdash {Q_{\forall }}$
but
$\mathbf {LC}{\varepsilon \tau } \vdash {Q_{\forall }}$
but
![]() ${\mathbf {Q}\mathbf {LC} + \mathit {CD}}\nvdash {Q_{\forall }}$
, and
${\mathbf {Q}\mathbf {LC} + \mathit {CD}}\nvdash {Q_{\forall }}$
, and
![]() $\mathbf {LC}_{m}{\varepsilon \tau } \vdash {\mathit {CD}^{\varepsilon \tau }}$
but
$\mathbf {LC}_{m}{\varepsilon \tau } \vdash {\mathit {CD}^{\varepsilon \tau }}$
but
![]() ${\mathbf {Q}\mathbf {LC}_{m}} \nvdash \mathit {CD}$
.⊣
${\mathbf {Q}\mathbf {LC}_{m}} \nvdash \mathit {CD}$
.⊣
However, we have:
Corollary 10.4. The second
![]() ${\varepsilon \tau }$
-theorem holds for finite-valued first-order Gödel logics
${\varepsilon \tau }$
-theorem holds for finite-valued first-order Gödel logics
![]() $\mathbf {G}_{m} = \mathbf {Q}\mathbf {LC}_{m} + \mathit {CD}$
.
$\mathbf {G}_{m} = \mathbf {Q}\mathbf {LC}_{m} + \mathit {CD}$
.
Proof. By Proposition 10.2, as
![]() $\mathbf {G}_{m}$
proves
$\mathbf {G}_{m}$
proves
![]() $\mathit {CD}$
,
$\mathit {CD}$
,
![]() $Q_{\exists }$
, and
$Q_{\exists }$
, and
![]() $Q_{\forall }$
, and has the extended first
$Q_{\forall }$
, and has the extended first
![]() ${\varepsilon \tau }$
-theorem.⊣
${\varepsilon \tau }$
-theorem.⊣
Herbrand’s theorem also yields other results, for instance, the following.
Proposition 10.5. Suppose
![]() $\mathbf {Q}\mathbf {L} +\mathit {Ax}_{1} \subseteq \mathbf {Q}\mathbf {L} + \mathit {Ax}_{2}$
are intermediate predicate logics. If Herbrand’s theorem holds in
$\mathbf {Q}\mathbf {L} +\mathit {Ax}_{1} \subseteq \mathbf {Q}\mathbf {L} + \mathit {Ax}_{2}$
are intermediate predicate logics. If Herbrand’s theorem holds in
![]() $\mathbf {Q}\mathbf {L} + \mathit {Ax}_{2}$
for existential formulas A, then
$\mathbf {Q}\mathbf {L} + \mathit {Ax}_{2}$
for existential formulas A, then
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1} \vdash A$
iff
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1} \vdash A$
iff
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{2} \vdash A$
. The result also holds for prenex formulas A if
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{2} \vdash A$
. The result also holds for prenex formulas A if
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1} \vdash \mathit {CD}$
.
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1} \vdash \mathit {CD}$
.
Proof. The “only if” direction is trivial since
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1} \subseteq \mathbf {Q}\mathbf {L}+\mathit {Ax}_{2}$
. For the “if” direction, assume
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1} \subseteq \mathbf {Q}\mathbf {L}+\mathit {Ax}_{2}$
. For the “if” direction, assume
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{2} \vdash A$
. Then there is a Herbrand disjunction
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{2} \vdash A$
. Then there is a Herbrand disjunction
![]() $A^{\prime }$
of A provable in
$A^{\prime }$
of A provable in
![]() $\mathbf {L}$
and hence in
$\mathbf {L}$
and hence in
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1}$
. Since
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1}$
. Since
![]() $\mathbf {Q}\mathbf {H} \vdash A^{\prime } \mathbin {\rightarrow } A$
, also
$\mathbf {Q}\mathbf {H} \vdash A^{\prime } \mathbin {\rightarrow } A$
, also
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1} \vdash A$
.
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1} \vdash A$
.
Now suppose in addition that
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1} \vdash \mathit {CD}$
and
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1} \vdash \mathit {CD}$
and
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{2} \vdash A$
with A prenex. Then since
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{2} \vdash A$
with A prenex. Then since
![]() $\mathbf {Q}\mathbf {H} \vdash A \mathbin {\rightarrow } H(A)$
,
$\mathbf {Q}\mathbf {H} \vdash A \mathbin {\rightarrow } H(A)$
,
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{2} \vdash H(A)$
. By Herbrand’s theorem there is a Herbrand disjunction
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{2} \vdash H(A)$
. By Herbrand’s theorem there is a Herbrand disjunction
![]() $A^{\prime }$
and
$A^{\prime }$
and
![]() $\mathbf {L} \vdash A^{\prime }$
. From
$\mathbf {L} \vdash A^{\prime }$
. From
![]() $A^{\prime }$
,
$A^{\prime }$
,
![]() $\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1}$
proves A, using just intuitionistically valid inferences as well as
$\mathbf {Q}\mathbf {L}+\mathit {Ax}_{1}$
proves A, using just intuitionistically valid inferences as well as
![]() $\mathit {CD}$
.⊣
$\mathit {CD}$
.⊣
Corollary 10.6. The existential fragments of
![]() $\mathbf {Q}\mathbf {LC}$
and
$\mathbf {Q}\mathbf {LC}$
and
![]() $\mathbf {G}_{\mathbb {R}}$
agree.
$\mathbf {G}_{\mathbb {R}}$
agree.
Proof. Take
![]() $\mathbf {L} = \mathbf {LC}$
,
$\mathbf {L} = \mathbf {LC}$
,
![]() $\mathit {Ax}_{1} = \emptyset $
, and
$\mathit {Ax}_{1} = \emptyset $
, and
![]() $\mathit {Ax}_{2} = \mathit {CD}$
. Infinite-valued Gödel logic
$\mathit {Ax}_{2} = \mathit {CD}$
. Infinite-valued Gödel logic
![]() $\mathbf {G}_{\mathbb {R}} = \mathbf {Q}\mathbf {LC}+\mathit {CD}$
has Herbrand’s theorem.⊣
$\mathbf {G}_{\mathbb {R}} = \mathbf {Q}\mathbf {LC}+\mathit {CD}$
has Herbrand’s theorem.⊣
Whenever the extended first
![]() ${\varepsilon \tau }$
-theorem holds for
${\varepsilon \tau }$
-theorem holds for
![]() $\mathbf {L}{\varepsilon \tau }$
, Herbrand’s theorem for existential formulas also holds for any intermediate predicate logic containing
$\mathbf {L}{\varepsilon \tau }$
, Herbrand’s theorem for existential formulas also holds for any intermediate predicate logic containing
![]() $\mathbf {L}$
. So, whenever an intermediate predicate logic
$\mathbf {L}$
. So, whenever an intermediate predicate logic
![]() $\mathbf {Q}\mathbf {L} +\mathit {Ax}_{1} \subseteq \mathbf {Q}\mathbf {L} +\mathit {Ax}_{2}$
, and
$\mathbf {Q}\mathbf {L} +\mathit {Ax}_{1} \subseteq \mathbf {Q}\mathbf {L} +\mathit {Ax}_{2}$
, and
![]() $\mathbf {L}{\varepsilon \tau }$
has the extended first
$\mathbf {L}{\varepsilon \tau }$
has the extended first
![]() ${\varepsilon \tau }$
-theorem, the purely existential fragments of
${\varepsilon \tau }$
-theorem, the purely existential fragments of
![]() $\mathbf {Q}\mathbf {L} +\mathit {Ax}_{1}$
and
$\mathbf {Q}\mathbf {L} +\mathit {Ax}_{1}$
and
![]() $\mathbf {Q}\mathbf {L} +\mathit {Ax}_{2}$
agree. For instance:
$\mathbf {Q}\mathbf {L} +\mathit {Ax}_{2}$
agree. For instance:
Corollary 10.7. The existential fragments of
![]() $\mathbf {Q}\mathbf {LC}_{m}$
and
$\mathbf {Q}\mathbf {LC}_{m}$
and
![]() $\mathbf {G}_{m} = \mathbf {Q}\mathbf {LC}_{m} + \mathit {CD}$
agree.
$\mathbf {G}_{m} = \mathbf {Q}\mathbf {LC}_{m} + \mathit {CD}$
agree.
By similar reasoning, the result holds for formulas of the form
![]() $\exists \vec x\, \lnot A(\vec x)$
for
$\exists \vec x\, \lnot A(\vec x)$
for
![]() $\mathbf {KC}$
and its extensions, since
$\mathbf {KC}$
and its extensions, since
![]() $\mathbf {KC}$
has the extended first
$\mathbf {KC}$
has the extended first
![]() ${\varepsilon \tau }$
-theorem for negated formulas (Theorem 9.8). By Proposition 6.7, the result can also be extended to formulas of the form
${\varepsilon \tau }$
-theorem for negated formulas (Theorem 9.8). By Proposition 6.7, the result can also be extended to formulas of the form
![]() $\forall \vec y\, B(\vec y) \mathbin {\rightarrow } \exists \vec x\,A(\vec x)$
.
$\forall \vec y\, B(\vec y) \mathbin {\rightarrow } \exists \vec x\,A(\vec x)$
.
11 Elimination of critical formulas using
 $\mathit {Lin}$
$\mathit {Lin}$
In the classical case, the first
![]() $\varepsilon $
-theorem is obtained by successively eliminating critical formulas belonging to a single
$\varepsilon $
-theorem is obtained by successively eliminating critical formulas belonging to a single
![]() $\varepsilon $
-term using excluded middle. In intermediate logics this is not available, but as we have seen in the proof of Theorem 8.6, critical formulas can also be eliminated using
$\varepsilon $
-term using excluded middle. In intermediate logics this is not available, but as we have seen in the proof of Theorem 8.6, critical formulas can also be eliminated using
![]() ${B_{m}}$
and
${B_{m}}$
and
![]() $\mathit {Lin}$
. And in fact, if a critical
$\mathit {Lin}$
. And in fact, if a critical
![]() ${\varepsilon \tau }$
-term e has only predicative critical formulas then it has a complete e-elimination set (by Lemma 8.5) already in
${\varepsilon \tau }$
-term e has only predicative critical formulas then it has a complete e-elimination set (by Lemma 8.5) already in
![]() $\mathbf {LC}$
, since only
$\mathbf {LC}$
, since only
![]() $\mathit {Lin}{}$
is required to eliminate predicative critical formulas. Thus, the procedure of the first
$\mathit {Lin}{}$
is required to eliminate predicative critical formulas. Thus, the procedure of the first
![]() ${\varepsilon \tau }$
-theorem terminates for all
${\varepsilon \tau }$
-theorem terminates for all
![]() ${\varepsilon \tau }$
-proofs in which no impredicative critical formulas occur during the successive elimination of critical formulas.
${\varepsilon \tau }$
-proofs in which no impredicative critical formulas occur during the successive elimination of critical formulas.
Proposition 11.1. If
![]() $\mathbf {LC}{\varepsilon \tau } \vdash E(u_{1},\dots ,u_{n})$
and there is an elimination sequence
$\mathbf {LC}{\varepsilon \tau } \vdash E(u_{1},\dots ,u_{n})$
and there is an elimination sequence
![]() $\langle \pi _{i}, \Lambda _{i}(e_{i}), T_{i}\rangle $
in which each formula in
$\langle \pi _{i}, \Lambda _{i}(e_{i}), T_{i}\rangle $
in which each formula in
![]() $\Lambda _{i}(e_{i})$
is predicative, then
$\Lambda _{i}(e_{i})$
is predicative, then
![]() $\mathbf {LC} \vdash \bigvee E(t_{i1}, \dots , t_{in})$
.
$\mathbf {LC} \vdash \bigvee E(t_{i1}, \dots , t_{in})$
.
Proof. By Proposition 9.2, since if in each step of the elimination sequence the eliminated critical formulas are all predicative, the elimination already works in
![]() $\mathbf {LC}{}$
by Lemma 8.5.⊣
$\mathbf {LC}{}$
by Lemma 8.5.⊣
So if there is a way to select critical
![]() ${\varepsilon \tau }$
-terms
${\varepsilon \tau }$
-terms
![]() $e_{i}$
successively for elimination in such way that the critical formulas belonging to
$e_{i}$
successively for elimination in such way that the critical formulas belonging to
![]() $e_{i}$
are always predicative, the extended first
$e_{i}$
are always predicative, the extended first
![]() ${\varepsilon \tau }$
-theorem holds in
${\varepsilon \tau }$
-theorem holds in
![]() $\mathbf {LC}{\varepsilon \tau }$
for a particular proof
$\mathbf {LC}{\varepsilon \tau }$
for a particular proof
![]() $\pi $
. However, it is hard to determine just by inspecting
$\pi $
. However, it is hard to determine just by inspecting
![]() $\pi $
if this is possible. For one, it is not sufficient that the critical formulas in
$\pi $
if this is possible. For one, it is not sufficient that the critical formulas in
![]() $\pi $
itself are all predicative: eliminating the critical formulas belonging to one critical
$\pi $
itself are all predicative: eliminating the critical formulas belonging to one critical
![]() ${\varepsilon \tau }$
-term may turn a remaining predicative critical formula into an impredicative one. For instance, consider
${\varepsilon \tau }$
-term may turn a remaining predicative critical formula into an impredicative one. For instance, consider
 $$ \begin{align*} E(x, y) & \equiv (A(f(y)) \mathbin{\rightarrow} A(x)) \land (B(g(x)) \mathbin{\rightarrow} B(y)),\\ e_{A} & \equiv \varepsilon_{x}\,A(x),\\ e_{B} & \equiv \varepsilon_{y}\,B(y). \end{align*} $$
$$ \begin{align*} E(x, y) & \equiv (A(f(y)) \mathbin{\rightarrow} A(x)) \land (B(g(x)) \mathbin{\rightarrow} B(y)),\\ e_{A} & \equiv \varepsilon_{x}\,A(x),\\ e_{B} & \equiv \varepsilon_{y}\,B(y). \end{align*} $$
Then
![]() ${D(e_{A}, e_{B})}$
has an
${D(e_{A}, e_{B})}$
has an
![]() ${\mathbf {LC}{\varepsilon \tau }}$
proof, since it is the conjunction of the critical formulas
${\mathbf {LC}{\varepsilon \tau }}$
proof, since it is the conjunction of the critical formulas
 $$ \begin{align*} & A(f(e_{B})) \mathbin{\rightarrow} A(e_{A}),\\ & B(g(e_{A})) \mathbin{\rightarrow} B(e_{B}), \end{align*} $$
$$ \begin{align*} & A(f(e_{B})) \mathbin{\rightarrow} A(e_{A}),\\ & B(g(e_{A})) \mathbin{\rightarrow} B(e_{B}), \end{align*} $$
which are both predicative. If we first eliminate
![]() ${e_{A}}$
we would replace
${e_{A}}$
we would replace
![]() ${e_{A}}$
by
${e_{A}}$
by
![]() ${f(e_{B})}$
in the second, resulting in
${f(e_{B})}$
in the second, resulting in
which is impredicative. Similarly, eliminating
![]() $e_{B}$
leaves the impredicative
$e_{B}$
leaves the impredicative
So no elimination sequence resulting in only predicative critical formulas at every step is possible.
Of course, if the term t in a critical formula
![]() $A(t) \mathbin {\rightarrow } A(e)$
contains no
$A(t) \mathbin {\rightarrow } A(e)$
contains no
![]() ${\varepsilon \tau }$
-term at all, it is predicative, and replacing some
${\varepsilon \tau }$
-term at all, it is predicative, and replacing some
![]() ${\varepsilon \tau }$
-term
${\varepsilon \tau }$
-term
![]() $e^{\prime }$
in it by a term
$e^{\prime }$
in it by a term
![]() $t^{\prime }$
cannot result in an impredicative critical formula. Let us call such critical formulas weak.
$t^{\prime }$
cannot result in an impredicative critical formula. Let us call such critical formulas weak.
Definition 11.2. A critical formula
![]() $A(t) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x))$
resp.
$A(t) \mathbin {\rightarrow } A(\varepsilon _{x}\,A(x))$
resp.
![]() $A(\tau _{x}\,A(x)) \mathbin {\rightarrow } A(t)$
is weak in
$A(\tau _{x}\,A(x)) \mathbin {\rightarrow } A(t)$
is weak in
![]() $\pi $
if t does not contain any critical
$\pi $
if t does not contain any critical
![]() $\varepsilon $
- or
$\varepsilon $
- or
![]() $\tau $
-term of
$\tau $
-term of
![]() $\pi $
.
$\pi $
.
If the critical formulas in
![]() $\pi $
are all weak, there is an elimination sequence.
$\pi $
are all weak, there is an elimination sequence.
Proposition 11.3. Suppose
![]() $\mathbf {LC}{\varepsilon \tau } \vdash E(e_{1}, \dots , e_{n})$
with a proof in which all critical formulas are weak. Then there are terms
$\mathbf {LC}{\varepsilon \tau } \vdash E(e_{1}, \dots , e_{n})$
with a proof in which all critical formulas are weak. Then there are terms
![]() $t_{i}^{j}$
such that
$t_{i}^{j}$
such that
![]() $\mathbf {LC} \vdash \bigvee _{j} E(t_{1}^{j}, \dots , t_{n}^{j})$
.
$\mathbf {LC} \vdash \bigvee _{j} E(t_{1}^{j}, \dots , t_{n}^{j})$
.
Proof. Take a critical
![]() ${\varepsilon \tau }$
-term e of maximum degree among those of maximal rank in
${\varepsilon \tau }$
-term e of maximum degree among those of maximal rank in
![]() $\pi $
, let
$\pi $
, let
![]() $\Gamma (e)$
be the critical formulas belonging to e,
$\Gamma (e)$
be the critical formulas belonging to e,
![]() $\Gamma $
the remaining critical formulas, and suppose the end-formula is
$\Gamma $
the remaining critical formulas, and suppose the end-formula is
![]() $D(e)$
. Since all critical formulas
$D(e)$
. Since all critical formulas
![]() $A(u) \mathbin {\rightarrow } A(e)$
(or
$A(u) \mathbin {\rightarrow } A(e)$
(or
![]() $A(e) \mathbin {\rightarrow } A(u)$
) are weak, e does not occur in u, i.e., all critical formulas in
$A(e) \mathbin {\rightarrow } A(u)$
) are weak, e does not occur in u, i.e., all critical formulas in
![]() $\Gamma (e)$
are predicative. By Lemma 8.5, e has an e-elimination set T, and correspondingly
$\Gamma (e)$
are predicative. By Lemma 8.5, e has an e-elimination set T, and correspondingly
![]() $\Gamma [T] \vdash _{\mathbf {LC}} \bigvee _{t} D(t)$
. However, since the critical formulas in
$\Gamma [T] \vdash _{\mathbf {LC}} \bigvee _{t} D(t)$
. However, since the critical formulas in
![]() $\Gamma $
are also weak, they do not contain e; hence
$\Gamma $
are also weak, they do not contain e; hence
![]() $\Gamma [T] = \Gamma $
. The result follows by the same inductive proof as the first
$\Gamma [T] = \Gamma $
. The result follows by the same inductive proof as the first
![]() ${\varepsilon \tau }$
-theorem.⊣
${\varepsilon \tau }$
-theorem.⊣
The extended first
![]() ${\varepsilon \tau }$
-theorem guarantees the existence of Herbrand disjunctions for existential theorems, i.e., if
${\varepsilon \tau }$
-theorem guarantees the existence of Herbrand disjunctions for existential theorems, i.e., if
![]() $E \equiv \exists x_{1}\dots x_{n} D(x_{1}, \dots , x_{n})$
and
$E \equiv \exists x_{1}\dots x_{n} D(x_{1}, \dots , x_{n})$
and
![]() $\vdash E$
then
$\vdash E$
then
![]() $\vdash \bigvee _{i} D(t_{1i}, \dots , t_{ni})$
. The existence of a Herbrand disjunction, conversely, guarantees the existence of a proof of
$\vdash \bigvee _{i} D(t_{1i}, \dots , t_{ni})$
. The existence of a Herbrand disjunction, conversely, guarantees the existence of a proof of
![]() $E^{\varepsilon \tau }$
for which a predicative elimination sequence exists.
$E^{\varepsilon \tau }$
for which a predicative elimination sequence exists.
Proposition 11.4. If
![]() $\vdash \bigvee _{i} D(t_{1i}, \dots , t_{ni})$
then there is an
$\vdash \bigvee _{i} D(t_{1i}, \dots , t_{ni})$
then there is an
![]() ${\varepsilon \tau }$
-derivation of
${\varepsilon \tau }$
-derivation of
![]() $[\exists x_{1}\dots \exists x_{n}\,D(x_{1}, \dots , x_{n})]^{\varepsilon \tau }$
for which a predicative elimination sequence exists.
$[\exists x_{1}\dots \exists x_{n}\,D(x_{1}, \dots , x_{n})]^{\varepsilon \tau }$
for which a predicative elimination sequence exists.
Proof. We give an example only. Suppose
![]() $\mathbf {LC} \vdash D(s_{1}, t_{1}) \lor D(s_{2}, t_{2})$
. First, consider
$\mathbf {LC} \vdash D(s_{1}, t_{1}) \lor D(s_{2}, t_{2})$
. First, consider
Then both
 $$ \begin{align*} C_{1}(e(s_{1})) & \equiv D(s_{1}, t_{1}) \mathbin{\rightarrow} D(s_{1}, e(s_{1})) \text{ and}\\ C_{2}(e(s_{2})) & \equiv D(s_{2}, t_{1}) \mathbin{\rightarrow} D(s_{2}, e(s_{2})) \end{align*} $$
$$ \begin{align*} C_{1}(e(s_{1})) & \equiv D(s_{1}, t_{1}) \mathbin{\rightarrow} D(s_{1}, e(s_{1})) \text{ and}\\ C_{2}(e(s_{2})) & \equiv D(s_{2}, t_{1}) \mathbin{\rightarrow} D(s_{2}, e(s_{2})) \end{align*} $$
are predicative critical formulas. Since
![]() $\mathbf {LC} \vdash D(s_{1}, t_{1}) \lor D(s_{2}, t_{2})$
we get from them
$\mathbf {LC} \vdash D(s_{1}, t_{1}) \lor D(s_{2}, t_{2})$
we get from them
![]() ${D(s_{1}, e(s_{1})) \lor D(s_{2}, s_{2})}$
. Now let
${D(s_{1}, e(s_{1})) \lor D(s_{2}, s_{2})}$
. Now let
 $$ \begin{align*} e^{\prime} & \equiv \varepsilon_{x}\,D(x, e(x)),\\ C_{3}(e^{\prime}) & \equiv D(s_{1}, e(s_{1})) \mathbin{\rightarrow} D(e^{\prime}, e(e^{\prime})),\\ C_{4}(e^{\prime}) & \equiv D(s_{2}, e(s_{2})) \mathbin{\rightarrow} D(e^{\prime}, e(e^{\prime})), \end{align*} $$
$$ \begin{align*} e^{\prime} & \equiv \varepsilon_{x}\,D(x, e(x)),\\ C_{3}(e^{\prime}) & \equiv D(s_{1}, e(s_{1})) \mathbin{\rightarrow} D(e^{\prime}, e(e^{\prime})),\\ C_{4}(e^{\prime}) & \equiv D(s_{2}, e(s_{2})) \mathbin{\rightarrow} D(e^{\prime}, e(e^{\prime})), \end{align*} $$
are also predicative critical formulas. Together we have a proof of
![]() $D(e^{\prime }, e(e^{\prime })) \equiv [\exists x\exists y D(x,y)]^{\varepsilon \tau }$
. Then
$D(e^{\prime }, e(e^{\prime })) \equiv [\exists x\exists y D(x,y)]^{\varepsilon \tau }$
. Then
 $$ \begin{align*} & \langle\{C_{3}(e^{\prime}), C_{4}(e^{\prime})\}, \{s_{1}, s_{2}\}\rangle,\\ & \langle\{C(_{1}(e(s_{1})))\}, \{t_{1}\}\rangle,\\ & \langle \{C(_{2}(e(s_{2})))\},\{t_{2}\}\rangle, \end{align*} $$
$$ \begin{align*} & \langle\{C_{3}(e^{\prime}), C_{4}(e^{\prime})\}, \{s_{1}, s_{2}\}\rangle,\\ & \langle\{C(_{1}(e(s_{1})))\}, \{t_{1}\}\rangle,\\ & \langle \{C(_{2}(e(s_{2})))\},\{t_{2}\}\rangle, \end{align*} $$
is an elimination sequence. In fact it is an elimination sequence following Hilbert’s ordering, since
![]() $e^{\prime }$
has higher rank than
$e^{\prime }$
has higher rank than
![]() $e(s_{1})$
and
$e(s_{1})$
and
![]() $e(s_{2})$
. In each step, only predicative critical formulas are generated. It produces the original Herbrand disjunction.⊣
$e(s_{2})$
. In each step, only predicative critical formulas are generated. It produces the original Herbrand disjunction.⊣
12 The first
 ${\varepsilon \tau }$
-theorem and order induction
${\varepsilon \tau }$
-theorem and order induction
In arithmetic, the usual methods for eliminating critical formulas based on the extended first
![]() $\varepsilon $
-theorem do not work; and so consistency proofs for systems based on the
$\varepsilon $
-theorem do not work; and so consistency proofs for systems based on the
![]() $\varepsilon $
-calculus use other methods such as the
$\varepsilon $
-calculus use other methods such as the
![]() $\varepsilon $
-substitution method (see [Reference Ackermann1, Reference Moser22]; the history of the two approaches is discussed in [Reference Zach29]). The methods developed for the extended first
$\varepsilon $
-substitution method (see [Reference Ackermann1, Reference Moser22]; the history of the two approaches is discussed in [Reference Zach29]). The methods developed for the extended first
![]() ${\varepsilon \tau }$
-theorem to eliminate predicative critical formulas from proofs in
${\varepsilon \tau }$
-theorem to eliminate predicative critical formulas from proofs in
![]() $\mathbf {LC}{\varepsilon \tau }$
above can, however, also be applied in classical theories of order (including arithmetic). Suppose T is a universal theory involving a relation
$\mathbf {LC}{\varepsilon \tau }$
above can, however, also be applied in classical theories of order (including arithmetic). Suppose T is a universal theory involving a relation
![]() $<$
, and consider the order induction rule
$<$
, and consider the order induction rule
![]() $\mathit {IR}_<$
,
$\mathit {IR}_<$
,

We denote by
![]() $\vdash _<$
the derivability relation generated by classical logic extended by
$\vdash _<$
the derivability relation generated by classical logic extended by
![]() $\mathit {IR}_<$
. The resulting system is equivalent to the result of adding to classical first-order logic the order induction principle for
$\mathit {IR}_<$
. The resulting system is equivalent to the result of adding to classical first-order logic the order induction principle for
![]() $<$
,
$<$
,
Proposition 12.1.
![]() $T \vdash _< A$
iff
$T \vdash _< A$
iff
![]() $T + \mathit {IP}_< \vdash A$
.
$T + \mathit {IP}_< \vdash A$
.
Proof. The “only if” direction follows by observing that if
 $$ \begin{align*} T & \vdash \forall x(x<y \mathbin{\rightarrow} A(x)) \mathbin{\rightarrow} A(y) \text{ then also}\\ T & \vdash \forall y(\forall x(x<y \mathbin{\rightarrow} A(x)) \mathbin{\rightarrow} A(y)), \end{align*} $$
$$ \begin{align*} T & \vdash \forall x(x<y \mathbin{\rightarrow} A(x)) \mathbin{\rightarrow} A(y) \text{ then also}\\ T & \vdash \forall y(\forall x(x<y \mathbin{\rightarrow} A(x)) \mathbin{\rightarrow} A(y)), \end{align*} $$
and so
![]() $A(t)$
follows from
$A(t)$
follows from
![]() $\mathit {IP}_<{}$
and
$\mathit {IP}_<{}$
and
![]() $\forall x\,A(x) \mathbin {\rightarrow } A(t)$
by modus ponens. For the “if” direction, let
$\forall x\,A(x) \mathbin {\rightarrow } A(t)$
by modus ponens. For the “if” direction, let
![]() $P_{A}$
be
$P_{A}$
be
Then by logic,
 $$ \begin{align*} & \vdash \forall u(u < v \mathbin{\rightarrow} A(u)) \mathbin{\rightarrow} (P_{A} \mathbin{\rightarrow} A(v)) \text{ and so}\\ & \vdash \forall u(u < v \mathbin{\rightarrow} (P_{A} \mathbin{\rightarrow} A(u))) \mathbin{\rightarrow} (P_{A} \mathbin{\rightarrow} A(v))\\ & \vdash_< P_{A} \mathbin{\rightarrow} A(z) \text{ by } \mathit{IR}_<, \text{ and consequently}\\ & \vdash_< P_{A} \mathbin{\rightarrow} \forall z\,A(z). \end{align*} $$
$$ \begin{align*} & \vdash \forall u(u < v \mathbin{\rightarrow} A(u)) \mathbin{\rightarrow} (P_{A} \mathbin{\rightarrow} A(v)) \text{ and so}\\ & \vdash \forall u(u < v \mathbin{\rightarrow} (P_{A} \mathbin{\rightarrow} A(u))) \mathbin{\rightarrow} (P_{A} \mathbin{\rightarrow} A(v))\\ & \vdash_< P_{A} \mathbin{\rightarrow} A(z) \text{ by } \mathit{IR}_<, \text{ and consequently}\\ & \vdash_< P_{A} \mathbin{\rightarrow} \forall z\,A(z). \end{align*} $$
Thus,
![]() $\vdash _< \mathit {IP}_<$
.⊣
$\vdash _< \mathit {IP}_<$
.⊣
Now consider the classical
![]() $\varepsilon $
-calculus extended by critical formulas of the form
$\varepsilon $
-calculus extended by critical formulas of the form
These critical formulas are obviously equivalent to Hilbert’s “critical formulas of the second form,”
![]() $A(t) \mathbin {\rightarrow } \varepsilon _{x}\,A(x) \le t$
, over a theory that proves that
$A(t) \mathbin {\rightarrow } \varepsilon _{x}\,A(x) \le t$
, over a theory that proves that
![]() $<$
is trichotomous. If A is derivable from T and ordinary critical formulas for
$<$
is trichotomous. If A is derivable from T and ordinary critical formulas for
![]() $\varepsilon $
-terms and critical formulas of this second kind, we write
$\varepsilon $
-terms and critical formulas of this second kind, we write
![]() $T \vdash _{<\varepsilon } A$
. The standard translation
$T \vdash _{<\varepsilon } A$
. The standard translation
![]() $A^{\varepsilon }$
of a formula A is defined as in Definition 3.3, except
$A^{\varepsilon }$
of a formula A is defined as in Definition 3.3, except
![]() $\forall x\,A(x)^{\varepsilon } \equiv A^{\varepsilon }(\varepsilon _{x}\,\lnot A^{\varepsilon }(x))$
. Then we can show:
$\forall x\,A(x)^{\varepsilon } \equiv A^{\varepsilon }(\varepsilon _{x}\,\lnot A^{\varepsilon }(x))$
. Then we can show:
Proposition 12.2. If
![]() $T \vdash _< A$
then
$T \vdash _< A$
then
![]() $T^{\varepsilon } \vdash _{<\varepsilon } A^{\varepsilon }$
.
$T^{\varepsilon } \vdash _{<\varepsilon } A^{\varepsilon }$
.
Proof. As in the proof of Lemma 3.5. We just have to deal with application of
![]() $\mathit {IR}_<$
. Suppose we have a derivation of the
$\mathit {IR}_<$
. Suppose we have a derivation of the
![]() $\varepsilon $
-translation of the premise of
$\varepsilon $
-translation of the premise of
![]() $\mathit {IR}_<$
,
$\mathit {IR}_<$
,
where
![]() $e(y) \equiv \varepsilon _{x}\,\lnot (x<y \mathbin {\rightarrow } A^{\varepsilon }(x))$
is the
$e(y) \equiv \varepsilon _{x}\,\lnot (x<y \mathbin {\rightarrow } A^{\varepsilon }(x))$
is the
![]() $\varepsilon $
-term used in the translation of
$\varepsilon $
-term used in the translation of
![]() $\forall x(x < y \mathbin {\rightarrow } A(x))$
. By substituting
$\forall x(x < y \mathbin {\rightarrow } A(x))$
. By substituting
![]() ${e^{\prime } \equiv \varepsilon _{z}\,\lnot A^{\varepsilon }(z)}$
for y throughout the proof, we obtain
${e^{\prime } \equiv \varepsilon _{z}\,\lnot A^{\varepsilon }(z)}$
for y throughout the proof, we obtain
Take the critical formula of second kind
![]() ${\lnot A^{\varepsilon }(t) \mathbin {\rightarrow } \lnot t < \varepsilon _{z}\,\lnot A^{\varepsilon }(z)}$
and let t be
${\lnot A^{\varepsilon }(t) \mathbin {\rightarrow } \lnot t < \varepsilon _{z}\,\lnot A^{\varepsilon }(z)}$
and let t be
![]() $e({e^{\prime }})$
. By contraposition, we have
$e({e^{\prime }})$
. By contraposition, we have
 $$ \begin{align*} & e(e^{\prime}) < e^{\prime} \mathbin{\rightarrow} A^{\varepsilon}(e(e^{\prime})) \text{ and so}\\ & A^{\varepsilon}(e^{\prime}) \end{align*} $$
$$ \begin{align*} & e(e^{\prime}) < e^{\prime} \mathbin{\rightarrow} A^{\varepsilon}(e(e^{\prime})) \text{ and so}\\ & A^{\varepsilon}(e^{\prime}) \end{align*} $$
by modus ponens. The conclusion of
![]() ${\mathit {IR}_<, A^{\varepsilon }(t)}$
, now follows from an ordinary critical formula belonging to
${\mathit {IR}_<, A^{\varepsilon }(t)}$
, now follows from an ordinary critical formula belonging to
![]() $\lnot A^{\varepsilon }(z)$
, viz.,
$\lnot A^{\varepsilon }(z)$
, viz.,
⊣
Arithmetic does not have a Herbrand theorem, and thus also no first
![]() $\varepsilon $
-theorem. However, Herbrand disjunctions exist for formulas
$\varepsilon $
-theorem. However, Herbrand disjunctions exist for formulas
![]() $\exists \vec x\, E(\vec x)$
iff the critical formulas belonging to the
$\exists \vec x\, E(\vec x)$
iff the critical formulas belonging to the
![]() $\varepsilon $
-terms
$\varepsilon $
-terms
![]() $e_{1}$
, …,
$e_{1}$
, …,
![]() $e_{n}$
in the standard
$e_{n}$
in the standard
![]() $\varepsilon $
-translation
$\varepsilon $
-translation
![]() $E^{\varepsilon }(e_{1}, \dots , e_{n})$
of
$E^{\varepsilon }(e_{1}, \dots , e_{n})$
of
![]() $\exists x_{1}\dots \exists x_{n}\,E(x_{1}, \dots , x_{n})$
can be eliminated by a predicative elimination sequence. This mirrors the situation in
$\exists x_{1}\dots \exists x_{n}\,E(x_{1}, \dots , x_{n})$
can be eliminated by a predicative elimination sequence. This mirrors the situation in
![]() $\mathbf {LC}{}$
discussed in Section 11. The proof that critical formulas can be eliminated if a predicative elimination sequence exists is similar. Corresponding to Lemma 8.4 we’ll need the following:
$\mathbf {LC}{}$
discussed in Section 11. The proof that critical formulas can be eliminated if a predicative elimination sequence exists is similar. Corresponding to Lemma 8.4 we’ll need the following:
Lemma 12.3. Let V be a finite set of variables and assume that
Then
![]() $T \vdash \bigvee _{x \in V} \bigwedge _{y \in V} \lnot y < x$
.
$T \vdash \bigvee _{x \in V} \bigwedge _{y \in V} \lnot y < x$
.
Proof. Suppose not. Then
![]() $T + \bigwedge _{x \in V} \bigvee _{y \in V} y < x$
would be satisfiable. Let
$T + \bigwedge _{x \in V} \bigvee _{y \in V} y < x$
would be satisfiable. Let
![]() $\mathfrak {M}$
and s be the corresponding structure and variable assignment. Fix
$\mathfrak {M}$
and s be the corresponding structure and variable assignment. Fix
![]() $x_{1} \in V$
. Since
$x_{1} \in V$
. Since
![]() $\mathfrak {M}, s \models \bigvee _{y \in V} y < x_{1}$
, for some
$\mathfrak {M}, s \models \bigvee _{y \in V} y < x_{1}$
, for some
![]() $x_{2} \in V$
,
$x_{2} \in V$
,
![]() $s(x_{2}) <^{\mathfrak {M}} s(x_{1})$
. Continuing, we obtain
$s(x_{2}) <^{\mathfrak {M}} s(x_{1})$
. Continuing, we obtain
![]() $x_{1}$
, …,
$x_{1}$
, …,
![]() $x_{n} \in V$
such that
$x_{n} \in V$
such that
![]() $s(x_{i+1}) <^{\mathfrak {M}} s(x_{i})$
for any n. Since V is finite, eventually
$s(x_{i+1}) <^{\mathfrak {M}} s(x_{i})$
for any n. Since V is finite, eventually
![]() $x_{i} \equiv x_{i+k}$
, contradicting the assumption that any model of T makes
$x_{i} \equiv x_{i+k}$
, contradicting the assumption that any model of T makes
![]() $<$
irreflexive and transitive.⊣
$<$
irreflexive and transitive.⊣
Theorem 12.4. Suppose T is as in Lemma 12.3. Then
![]() $T \vdash \bigvee _{i=1}^{k} E(t_{1i}, \dots , t_{ni})$
for some terms
$T \vdash \bigvee _{i=1}^{k} E(t_{1i}, \dots , t_{ni})$
for some terms
![]() $t_{ji}$
iff there is a derivation of
$t_{ji}$
iff there is a derivation of
![]() $E^{\varepsilon }(e_{1}, \dots , e_{n})$
which has a predicative elimination sequence.
$E^{\varepsilon }(e_{1}, \dots , e_{n})$
which has a predicative elimination sequence.
Proof. For the “only if” part, proceed as in the procedure outlined in the proof of Proposition 11.4. For the “if” part, we have to show that if the critical formulas belonging to an
![]() $\varepsilon $
-term are predicative, they can be eliminated. Without loss of generality we may assume that for each term
$\varepsilon $
-term are predicative, they can be eliminated. Without loss of generality we may assume that for each term
![]() $t_{i}$
, a corresponding critical formula of first and of second kind are both present. So suppose e is a critical
$t_{i}$
, a corresponding critical formula of first and of second kind are both present. So suppose e is a critical
![]() $\varepsilon $
-term and
$\varepsilon $
-term and
![]() $\Theta , \Gamma , \Pi (e), \Pi ^{\prime }(e) \vdash _{<\varepsilon } D(e)$
where
$\Theta , \Gamma , \Pi (e), \Pi ^{\prime }(e) \vdash _{<\varepsilon } D(e)$
where
![]() $\Pi (e)$
and
$\Pi (e)$
and
![]() $\Pi ^{\prime }(e)$
consist of, respectively,
$\Pi ^{\prime }(e)$
consist of, respectively,
 $$ \begin{align*} A(t_{1}) & \mathbin{\rightarrow} A(e), & \dots, & & A(t_{m}) & \mathbin{\rightarrow} A(e), \\ A(t_{1}) & \mathbin{\rightarrow} \lnot t_{1} < e, & \dots,& & A(t_{m}) & \mathbin{\rightarrow} \lnot t_{m} < e, \end{align*} $$
$$ \begin{align*} A(t_{1}) & \mathbin{\rightarrow} A(e), & \dots, & & A(t_{m}) & \mathbin{\rightarrow} A(e), \\ A(t_{1}) & \mathbin{\rightarrow} \lnot t_{1} < e, & \dots,& & A(t_{m}) & \mathbin{\rightarrow} \lnot t_{m} < e, \end{align*} $$
and
![]() $\Theta $
consists of instances of formulas in T.
$\Theta $
consists of instances of formulas in T.
Let
![]() $W = \{t_{1}, \dots , t_{m}\}$
. If
$W = \{t_{1}, \dots , t_{m}\}$
. If
![]() $V \subseteq W$
, let
$V \subseteq W$
, let
![]() $C_{V}$
be
$C_{V}$
be
and let
![]() $\Pi _{V}(e)$
be the critical formulas with terms
$\Pi _{V}(e)$
be the critical formulas with terms
![]() $t_{i} \in V$
and
$t_{i} \in V$
and
![]() $\Pi _{W\setminus V}(e) = \Pi (e) \setminus \Pi _{V}(e)$
, and similarly for
$\Pi _{W\setminus V}(e) = \Pi (e) \setminus \Pi _{V}(e)$
, and similarly for
![]() $\Pi ^{\prime }_{V}(e)$
and
$\Pi ^{\prime }_{V}(e)$
and
![]() $\Pi ^{\prime }_{T\setminus V}(e)$
. Since
$\Pi ^{\prime }_{T\setminus V}(e)$
. Since
![]() $\lnot A(t) \vdash A(t) \mathbin {\rightarrow } B$
, we have
$\lnot A(t) \vdash A(t) \mathbin {\rightarrow } B$
, we have
![]() $C_{V} \vdash \Pi _{W\setminus V}(e)$
and
$C_{V} \vdash \Pi _{W\setminus V}(e)$
and
![]() $C_{V} \vdash \Pi ^{\prime }_{W\setminus V}(e)$
, and so
$C_{V} \vdash \Pi ^{\prime }_{W\setminus V}(e)$
, and so
Since the critical formulas in
![]() ${\Pi (e)}$
are predicative,
${\Pi (e)}$
are predicative,
![]() ${t_{i}}$
does not contain e and so
${t_{i}}$
does not contain e and so
![]() ${C_{V}[t_{i}/e] = C_{V}}$
. Since
${C_{V}[t_{i}/e] = C_{V}}$
. Since
![]() ${C_{V} \vdash A(t_{i})}$
for every
${C_{V} \vdash A(t_{i})}$
for every
![]() ${t_{i} \in V, C_{V} \vdash \Pi _{V}(t_{i})}$
. So we also have
${t_{i} \in V, C_{V} \vdash \Pi _{V}(t_{i})}$
. So we also have
for each
![]() ${t_{i} \in V}$
and consequently
${t_{i} \in V}$
and consequently
Since this is true for every
![]() ${V \subseteq W}$
, we get
${V \subseteq W}$
, we get
if we let
![]() ${\Xi = \{ B_{V}:V \subseteq W\}}$
where
${\Xi = \{ B_{V}:V \subseteq W\}}$
where
![]() ${B_{V}}$
is
${B_{V}}$
is
![]() ${\bigvee _{t \in V} \bigwedge _{u\in V} (A(u) \mathbin {\rightarrow } \lnot u < t)}$
. Now
${\bigvee _{t \in V} \bigwedge _{u\in V} (A(u) \mathbin {\rightarrow } \lnot u < t)}$
. Now
![]() ${\bigvee _{V \subseteq W} C_{V}}$
is itself provable in classical logic. So as the result of one elimination step, we get
${\bigvee _{V \subseteq W} C_{V}}$
is itself provable in classical logic. So as the result of one elimination step, we get
If there is a predicative elimination sequence, we have in the end terms
![]() ${t_{ij}}$
such that
${t_{ij}}$
such that
 $$ \begin{align*} \hspace{15pc} \Theta^{\prime}, \Xi^{\prime} &\vdash_{<\varepsilon} \bigvee_{i=1}^{k} E(t_{1i}, \dots, t_{ni}), \end{align*} $$
$$ \begin{align*} \hspace{15pc} \Theta^{\prime}, \Xi^{\prime} &\vdash_{<\varepsilon} \bigvee_{i=1}^{k} E(t_{1i}, \dots, t_{ni}), \end{align*} $$
where
![]() ${\Theta ^{\prime }}$
are all the instances of formulas of T produced in the elimination, and
${\Theta ^{\prime }}$
are all the instances of formulas of T produced in the elimination, and
![]() ${\Xi ^{\prime }}$
are all the formulas of the form
${\Xi ^{\prime }}$
are all the formulas of the form
![]() ${B_{V}}$
, possibly with epsilon terms replaced by other terms.
${B_{V}}$
, possibly with epsilon terms replaced by other terms.
![]() ${T \vdash A}$
for each
${T \vdash A}$
for each
![]() ${A \in \Theta ^{\prime }}$
. By Lemma 12.3,
${A \in \Theta ^{\prime }}$
. By Lemma 12.3,
and so each formula
![]() ${B_{V} \in \Xi ^{\prime }}$
is also provable from T. Together we have,
${B_{V} \in \Xi ^{\prime }}$
is also provable from T. Together we have,
 $$ \begin{align*} \hspace{15.5pc} T &\vdash \bigvee_{i=1}^{k} E(t_{1i}, \dots, t_{ni}). \\[-40pt] \end{align*} $$
$$ \begin{align*} \hspace{15.5pc} T &\vdash \bigvee_{i=1}^{k} E(t_{1i}, \dots, t_{ni}). \\[-40pt] \end{align*} $$
⊣
13 Open problems
We have investigated the
![]() ${\varepsilon \tau }$
-calculi for intermediate logics, with a focus on the extended first
${\varepsilon \tau }$
-calculi for intermediate logics, with a focus on the extended first
![]() ${\varepsilon \tau }$
-theorem. We showed that the only intermediate logics with an extended first
${\varepsilon \tau }$
-theorem. We showed that the only intermediate logics with an extended first
![]() ${\varepsilon \tau }$
-theorem are the finite-valued Gödel logics
${\varepsilon \tau }$
-theorem are the finite-valued Gödel logics
![]() $\mathbf {LC}_{m}$
, but obtained partial results for formulas of specific form or with specific kinds of proofs for other intermediate logics.
$\mathbf {LC}_{m}$
, but obtained partial results for formulas of specific form or with specific kinds of proofs for other intermediate logics.
The natural next question to investigate is the second
![]() $\varepsilon $
-theorem, i.e., to investigate extended
$\varepsilon $
-theorem, i.e., to investigate extended
![]() ${\varepsilon \tau }$
-calculi for intermediate predicate logics and characterize those logics for which the extended
${\varepsilon \tau }$
-calculi for intermediate predicate logics and characterize those logics for which the extended
![]() ${\varepsilon \tau }$
-calculus is conservative. We have shown that
${\varepsilon \tau }$
-calculus is conservative. We have shown that
![]() $\mathbf {L}{\varepsilon \tau }$
proves all quantifier shifts, so
$\mathbf {L}{\varepsilon \tau }$
proves all quantifier shifts, so
![]() $\mathbf {L}{\varepsilon \tau }$
is not conservative over any
$\mathbf {L}{\varepsilon \tau }$
is not conservative over any
![]() $\mathbf {Q}\mathbf {L}$
where these are not provable. Note that this question is not automatically settled by the answer to the question of which logics have the extended first
$\mathbf {Q}\mathbf {L}$
where these are not provable. Note that this question is not automatically settled by the answer to the question of which logics have the extended first
![]() ${\varepsilon \tau }$
-theorem. Rather, it is a question orthogonal and requires other proof systems for a proper investigation, such as sequent calculi for
${\varepsilon \tau }$
-theorem. Rather, it is a question orthogonal and requires other proof systems for a proper investigation, such as sequent calculi for
![]() ${\varepsilon \tau }$
-terms. For instance, Theorem 5.4 of [Reference Aguilera and Baaz2] shows that the standard translation
${\varepsilon \tau }$
-terms. For instance, Theorem 5.4 of [Reference Aguilera and Baaz2] shows that the standard translation
![]() $\Gamma \Rightarrow D^{\varepsilon }$
of a sequent
$\Gamma \Rightarrow D^{\varepsilon }$
of a sequent
![]() $\Gamma \Rightarrow D$
is provable in a sequent calculus
$\Gamma \Rightarrow D$
is provable in a sequent calculus
![]() $\mathbf {LJ}^{\varepsilon }$
for intuitionistic logic iff
$\mathbf {LJ}^{\varepsilon }$
for intuitionistic logic iff
![]() $\Gamma \Rightarrow D$
is provable in a special version
$\Gamma \Rightarrow D$
is provable in a special version
![]() $\mathbf {LJ}^{++}$
of intuitionistic sequent calculus which is globally sound but allows violation of the eigenvariable condition.
$\mathbf {LJ}^{++}$
of intuitionistic sequent calculus which is globally sound but allows violation of the eigenvariable condition.
![]() $\mathbf {LJ}^{++}$
in turn proves
$\mathbf {LJ}^{++}$
in turn proves
![]() $\Gamma \Rightarrow D$
iff
$\Gamma \Rightarrow D$
iff
![]() $\mathbf {LJ} + \mathit {CD} + Q_{\forall } + Q_{\exists } \vdash \Gamma \Rightarrow D$
(Proposition 4.4). In other words, the second
$\mathbf {LJ} + \mathit {CD} + Q_{\forall } + Q_{\exists } \vdash \Gamma \Rightarrow D$
(Proposition 4.4). In other words, the second
![]() $\varepsilon $
-theorem holds for intuitionistic predicate logic with all quantifier shifts.
$\varepsilon $
-theorem holds for intuitionistic predicate logic with all quantifier shifts.
The methods used here are closely related to the study of the behavior of Skolem functions in intermediate logics (of which
![]() ${\varepsilon \tau }$
-terms are in many ways a syntactic variant); see, e.g., [Reference Iemhoff18]. As mentioned in the introduction, other approaches to adding
${\varepsilon \tau }$
-terms are in many ways a syntactic variant); see, e.g., [Reference Iemhoff18]. As mentioned in the introduction, other approaches to adding
![]() $\varepsilon $
-operators to intuitionistic logic yield systems that are conservative over the original logic. Work on Skolemization in intuitionistic logic is relevant here, and suggests that conservative
$\varepsilon $
-operators to intuitionistic logic yield systems that are conservative over the original logic. Work on Skolemization in intuitionistic logic is relevant here, and suggests that conservative
![]() $\varepsilon $
-calculi can be obtained by introducing existence predicates. The proof-theoretic approaches in the literature would benefit also from a complementary model-theoretic study. A Kripke-style semantics for
$\varepsilon $
-calculi can be obtained by introducing existence predicates. The proof-theoretic approaches in the literature would benefit also from a complementary model-theoretic study. A Kripke-style semantics for
![]() ${\varepsilon \tau }$
-terms, with or without existence predicate, is still lacking (but see [Reference DeVidi12] for a semantics based on Heyting algebras).
${\varepsilon \tau }$
-terms, with or without existence predicate, is still lacking (but see [Reference DeVidi12] for a semantics based on Heyting algebras).
In Section 11 we gave sufficient conditions for when
![]() ${\varepsilon \tau }$
-terms can be eliminated from a proof
${\varepsilon \tau }$
-terms can be eliminated from a proof
![]() $\pi $
in
$\pi $
in
![]() $\mathbf {LC}{\varepsilon \tau }$
. Are there better (weaker) criteria that apply to more proofs? For instance, there may be certain kinds of orderings such that if the critical
$\mathbf {LC}{\varepsilon \tau }$
. Are there better (weaker) criteria that apply to more proofs? For instance, there may be certain kinds of orderings such that if the critical
![]() ${\varepsilon \tau }$
-terms in
${\varepsilon \tau }$
-terms in
![]() $\pi $
and corresponding “witness terms” can be put into such an ordering, an elimination sequence in which only predicative critical formulas exists. The same question applies for the parallel condition in arithmetical theories in Theorem 12.4.
$\pi $
and corresponding “witness terms” can be put into such an ordering, an elimination sequence in which only predicative critical formulas exists. The same question applies for the parallel condition in arithmetical theories in Theorem 12.4.
Acknowledgments
The authors would like to thank Guram Bezhanishvili, David Gabelaia, and the reviewer for the Journal. The research of the first author was supported by the Austrian Science Fund in projects P31063, I4427, and P31955. The research of the second author was supported by the Natural Sciences and Engineering Council of Canada. The authors acknowledge TU Wien Bibliothek for financial support through its Open Access Funding Program.