Published online by Cambridge University Press: 12 February 2018
In [12], Schwichtenberg showed that the System T definable functionals are closed under a rule-like version Spector’s bar recursion of lowest type levels 0 and 1. More precisely, if the functional Y which controls the stopping condition of Spector’s bar recursor is T-definable, then the corresponding bar recursion of type levels 0 and 1 is already T-definable. Schwichtenberg’s original proof, however, relies on a detour through Tait’s infinitary terms and the correspondence between ordinal recursion for 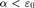 $\alpha < {\varepsilon _0}$ and primitive recursion over finite types. This detour makes it hard to calculate on given concrete system T input, what the corresponding system T output would look like. In this paper we present an alternative (more direct) proof based on an explicit construction which we prove correct via a suitably defined logical relation. We show through an example how this gives a straightforward mechanism for converting bar recursive definitions into T-definitions under the conditions of Schwichtenberg’s theorem. Finally, with the explicit construction we can also easily state a sharper result: if Y is in the fragment Ti then terms built from
$\alpha < {\varepsilon _0}$ and primitive recursion over finite types. This detour makes it hard to calculate on given concrete system T input, what the corresponding system T output would look like. In this paper we present an alternative (more direct) proof based on an explicit construction which we prove correct via a suitably defined logical relation. We show through an example how this gives a straightforward mechanism for converting bar recursive definitions into T-definitions under the conditions of Schwichtenberg’s theorem. Finally, with the explicit construction we can also easily state a sharper result: if Y is in the fragment Ti then terms built from 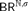 $BR^{\mathbb{N},\sigma } $ for this particular Y are definable in the fragment
$BR^{\mathbb{N},\sigma } $ for this particular Y are definable in the fragment 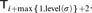 ${T_{i + {\rm{max}}\left\{ {1,{\rm{level}}\left( \sigma \right)} \right\} + 2}}$.
${T_{i + {\rm{max}}\left\{ {1,{\rm{level}}\left( \sigma \right)} \right\} + 2}}$.