Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-23T12:00:30.997Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGEBRAIC EXPANSIONS OF LOGICS

Part of: Distributive lattices Algebraic logic Ordered structures Boolean algebras (Boolean rings)

Published online by Cambridge University Press:  22 June 2022

MIGUEL CAMPERCHOLI ,
DIEGO NICOLÁS CASTAÑO ,
JOSÉ PATRICIO DÍAZ VARELA  and
JOAN GISPERT
MIGUEL CAMPERCHOLI*
Affiliation:
FACULTAD DE MATEMÁTICA, ASTRONOMÍA Y FÍSICA UNIVERSIDAD NACIONAL DE CÓRDOBA CIEM—CONICET CÓRDOBA, ARGENTINA
DIEGO NICOLÁS CASTAÑO
Affiliation:
DEPARTAMENTO DE MATEMÁTICA UNIVERSIDAD NACIONAL DEL SUR BAHÍA BLANCA, ARGENTINA and INSTITUTO DE MATEMÁTICA (INMABB) UNIVERSIDAD NACIONAL DEL SUR (UNS)-CONICET BAHÍA BLANCA, ARGENTINA E-mail: diego.castano@uns.edu.ar E-mail: usdiavar@criba.edu.ar
JOSÉ PATRICIO DÍAZ VARELA
Affiliation:
DEPARTAMENTO DE MATEMÁTICA UNIVERSIDAD NACIONAL DEL SUR BAHÍA BLANCA, ARGENTINA and INSTITUTO DE MATEMÁTICA (INMABB) UNIVERSIDAD NACIONAL DEL SUR (UNS)-CONICET BAHÍA BLANCA, ARGENTINA E-mail: diego.castano@uns.edu.ar E-mail: usdiavar@criba.edu.ar
JOAN GISPERT
Affiliation:
DEPARTAMENT DE MATEMÀTIQUES I INFORMÀTICA INSTITUT DE MATEMÀTIQUES DE LA UNIVERSITAT DE BARCELONA (IMUB) BARCELONA GRADUATE SCHOOL OF MATHEMATICS (BGSMATH) UNIVERSITAT DE BARCELONA (UB) BARCELONA, SPAIN E-mail: jgispertb@ub.edu
*
E-mail: camper@famaf.unc.edu.ar
Get access Rights & Permissions [Opens in a new window]

Abstract

An algebraically expandable (AE) class is a class of algebraic structures axiomatizable by sentences of the form 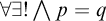$\forall \exists ! \mathop{\boldsymbol {\bigwedge }}\limits p = q$ . For a logic L algebraized by a quasivariety $\mathcal {Q}$ we show that the AE-subclasses of $\mathcal {Q}$ correspond to certain natural expansions of L, which we call algebraic expansions. These turn out to be a special case of the expansions by implicit connectives studied by X. Caicedo. We proceed to characterize all the AE-subclasses of abelian 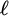$\ell $ -groups and perfect MV-algebras, thus fully describing the algebraic expansions of their associated logics.

Keywords

expansionslattice-ordered groupsequationally definable functionsalgebraic functionsMV-algebras

MSC classification

Primary: 03G27: Abstract algebraic logic
Secondary: 06D35: MV-algebras 06F20: Ordered abelian groups, Riesz groups, ordered linear spaces
Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 1 , March 2023 , pp. 74 - 92
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belluce, L. P., Di Nola, A., and Gerla, B., Perfect MV-algebras and their logic . Applied Categorical Structures , vol. 15 (2007), nos. 1–2, pp. 135–151.CrossRefGoogle Scholar
Birkhoff, G., Lattice Theory , American Mathematical Society, New York, 1940.Google Scholar
Blok, W. J. and Ferreirim, I. M. A., On the structure of hoops . Algebra Universalis , vol. 43 (2000), nos. 2–3, pp. 233–257.CrossRefGoogle Scholar
Burris, S. and Sankappanavar, H., A Course in Universal Algebra , Graduate Texts in Mathematics, vol. 78, Springer, New York, 1981.CrossRefGoogle Scholar
Caicedo, X., Implicit connectives of algebraizable logics . Studia Logica , vol. 78 (2004), nos. 1–2, pp. 155–170.Google Scholar
Caicedo, X., Implicit operations in MV-algebras and the connectives of Łukasiewicz logic , Algebraic and Proof-Theoretic Aspects of Non-Classical Logics , Lecture Notes in Computer Science, vol. 4460, Springer, Berlin–Heidelberg, 2007.CrossRefGoogle Scholar
Caicedo, X. and Cignoli, R., An algebraic approach to intuitionistic connectives, this Journal, vol. 66 (2001), no. 4, pp. 1620–1636.Google Scholar
Campercholi, M., Algebraically expandable classes of Heyting algebras, preprint, 2010.CrossRefGoogle Scholar
Campercholi, M., Algebraically expandable classes of implication algebras . International Journal of Algebra and Computation , vol. 20 (2010), no. 5, pp. 605–617.Google Scholar
Campercholi, M. and Vaggione, D., Algebraically expandable classes . Algebra Universalis , vol. 61 (2009), no. 2, pp. 151–186.CrossRefGoogle Scholar
Campercholi, M. and Vaggione, D., Algebraic functions . Studia Logica , vol. 98 (2011), nos. 1–2, pp. 285–306.CrossRefGoogle Scholar
Cignoli, R. L. O., D’Ottaviano, I. M. L., and Mundici, D., Algebraic Foundations of Many-Valued Reasoning , Trends in Logic—Studia Logica Library, vol. 7, Kluwer Academic, Dordrecht, 2000.CrossRefGoogle Scholar
Di Nola, A. and Lettieri, A., Perfect MV-algebras are categorically equivalent to abelian $l$ -groups . Studia Logica , vol. 53 (1994), no. 3, pp. 417–432.CrossRefGoogle Scholar
Ferreirim, I. M. A., On Varieties and Quasivarieties of Hoops and Their Reducts , ProQuest LLC, Ann Arbor, 1992, Ph.D. thesis, University of Illinois at Chicago.Google Scholar
Font, J. M., Abstract Algebraic Logic: An Introductory Textbook , Studies in Logic: Mathematical Logic and Foundations, vol. 60, College Publications, London, 2016.Google Scholar
Galli, A., Lewin, R. A., and Sagastume, M., The logic of equilibrium and abelian lattice ordered groups . Archive for Mathematical Logic , vol. 43 (2004), no. 2, pp. 141–158.CrossRefGoogle Scholar
Glass, A. M. W., Partially Ordered Groups , Series in Algebra, vol. 7, World Scientific, River Edge, 1999.CrossRefGoogle Scholar
Gramaglia, H. and Vaggione, D., Birkhoff-like sheaf representation for varieties of lattice expansions . Studia Logica , vol. 56 (1996), nos. 1–2, pp. 111–131. Special issue on Priestley duality.Google Scholar
Hodges, W., Model Theory , Encyclopedia of Mathematics and Its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Jónsson, B., Algebras whose congruence lattices are distributive . Mathematica Scandinavica , vol. 21 (1968), pp. 110–121.CrossRefGoogle Scholar
Metcalfe, G., Olivetti, N., and Gabbay, D., Sequent and hypersequent calculi for abelian and Łukasiewicz logics . ACM Transactions on Computational Logic , vol. 6 (2005), no. 3, pp. 578–613.CrossRefGoogle Scholar
Mundici, D., Interpretation of AF ${C}^{\ast }$ -algebras in Łukasiewicz sentential calculus . Journal of Functional Analysis , vol. 65 (1986), no. 1, pp. 15–63.CrossRefGoogle Scholar
Mundici, D., Mapping abelian $l$ -groups with strong unit one–one into MV algebras . Journal of Algebra , vol. 98 (1986), no. 1, pp. 76–81.CrossRefGoogle Scholar
Robinson, A., Complete Theories , North-Holland, Amsterdam, 1956.Google Scholar
Volger, H., Preservation theorems for limits of structures and global sections of sheaves of structures . Mathematische Zeitschrift , vol. 166 (1979), no. 1, pp. 27–54.CrossRefGoogle Scholar
Weinberg, E. C., Free lattice-ordered abelian groups. II . Mathematische Annalen , vol. 159 (1965), pp. 217–222.CrossRefGoogle Scholar