Article contents
RELATIONSHIPS BETWEEN COMPUTABILITY-THEORETIC PROPERTIES OF PROBLEMS
Published online by Cambridge University Press: 05 October 2020
Abstract
A problem is a multivalued function from a set of instances to a set of solutions. We consider only instances and solutions coded by sets of integers. A problem admits preservation of some computability-theoretic weakness property if every computable instance of the problem admits a solution relative to which the property holds. For example, cone avoidance is the ability, given a noncomputable set A and a computable instance of a problem 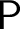 ${\mathsf {P}}$
, to find a solution relative to which A is still noncomputable.
${\mathsf {P}}$
, to find a solution relative to which A is still noncomputable.
In this article, we compare relativized versions of computability-theoretic notions of preservation which have been studied in reverse mathematics, and prove that the ones which were not already separated by natural statements in the literature actually coincide. In particular, we prove that it is equivalent to admit avoidance of one cone, of 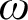 $\omega $
cones, of one hyperimmunity or of one non-
$\omega $
cones, of one hyperimmunity or of one non-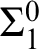 $\Sigma ^{0}_1$
definition. We also prove that the hierarchies of preservation of hyperimmunity and non-
$\Sigma ^{0}_1$
definition. We also prove that the hierarchies of preservation of hyperimmunity and non-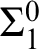 $\Sigma ^{0}_1$
definitions coincide. On the other hand, none of these notions coincide in a nonrelativized setting.
$\Sigma ^{0}_1$
definitions coincide. On the other hand, none of these notions coincide in a nonrelativized setting.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 1
- Cited by



