Article contents
The polynomial and linear hierarchies in models where the weak pigeonhole principle fails
Published online by Cambridge University Press: 12 March 2014
Abstract
We show, under the assumption that factoring is hard, that a model of PV exists in which the polynomial hierarchy does not collapse to the linear hierarchy; that a model of  exists in which NP is not in the second level of the linear hierarchy; and that a model of
exists in which NP is not in the second level of the linear hierarchy; and that a model of  exists in which the polynomial hierarchy collapses to the linear hierarchy.
exists in which the polynomial hierarchy collapses to the linear hierarchy.
Our methods are model-theoretic. We use the assumption about factoring to get a model in which the weak pigeonhole principle fails in a certain way, and then work with this failure to obtain our results.
As a corollary of one of the proofs, we also show that in  the failure of WPHP (for
the failure of WPHP (for 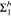 definable relations) implies that the strict version of PH does not collapse to a finite level.
definable relations) implies that the strict version of PH does not collapse to a finite level.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 4
- Cited by


