Article contents
P versus NP and computability theoretic constructions in complexity theory over algebraic structures
Published online by Cambridge University Press: 12 March 2014
Abstract
We show that there is a structure of countably infinite signature with P = N2P and a structure of finite signature with P = N1P and N1P ≠ N2P. We give a further example of a structure of finite signature with P ≠ N1P and N1P ≠ N1P. Together with a result from [10] this implies that for each possibility of P versus NP over structures there is an example of countably infinite signature. Then we show that for some finite 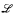 the class of
the class of 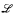 -structures with P = N1P is not closed under ultraproducts and obtain as corollaries that this class is not ∆-elementary and that the class of
-structures with P = N1P is not closed under ultraproducts and obtain as corollaries that this class is not ∆-elementary and that the class of 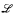 -structures with P ≠ N1P is not elementary. Finally we prove that for all ƒ dominating all polynomials there is a structure of finite signature with the following properties: P ≠ N1P, N1P ≠ N2P, the levels N2TIME(ni) of N2P and the levels N1TIME(ni) of N1P are different for different i, indeed DTIME(ni′) ⊈ N2TIME(ni) if i ′ > i; DTIME(ƒ) ⊈ N2P, and N2P ⊈ DEC. DEC is the class of recognizable sets with recognizable complements. So this is an example where the internal structure of N2P is analyzed in a more detailed way. In our proofs we use methods in the style of classical computability theory to construct structures except for one use of ultraproducts.
-structures with P ≠ N1P is not elementary. Finally we prove that for all ƒ dominating all polynomials there is a structure of finite signature with the following properties: P ≠ N1P, N1P ≠ N2P, the levels N2TIME(ni) of N2P and the levels N1TIME(ni) of N1P are different for different i, indeed DTIME(ni′) ⊈ N2TIME(ni) if i ′ > i; DTIME(ƒ) ⊈ N2P, and N2P ⊈ DEC. DEC is the class of recognizable sets with recognizable complements. So this is an example where the internal structure of N2P is analyzed in a more detailed way. In our proofs we use methods in the style of classical computability theory to construct structures except for one use of ultraproducts.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2004
References
REFERENCES
- 2
- Cited by


