No CrossRef data available.
Article contents
NSOP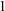 $_1$-LIKE INDEPENDENCE IN AECATS
$_1$-LIKE INDEPENDENCE IN AECATS
Published online by Cambridge University Press: 12 December 2022
Abstract
The classes stable, simple, and NSOP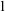 $_1$ in the stability hierarchy for first-order theories can be characterised by the existence of a certain independence relation. For each of them there is a canonicity theorem: there can be at most one nice independence relation. Independence in stable and simple first-order theories must come from forking and dividing (which then coincide), and for NSOP
$_1$ in the stability hierarchy for first-order theories can be characterised by the existence of a certain independence relation. For each of them there is a canonicity theorem: there can be at most one nice independence relation. Independence in stable and simple first-order theories must come from forking and dividing (which then coincide), and for NSOP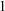 $_1$ theories it must come from Kim-dividing. We generalise this work to the framework of Abstract Elementary Categories (AECats) with the amalgamation property. These are a certain kind of accessible category generalising the category of (subsets of) models of some theory. We prove canonicity theorems for stable, simple, and NSOP
$_1$ theories it must come from Kim-dividing. We generalise this work to the framework of Abstract Elementary Categories (AECats) with the amalgamation property. These are a certain kind of accessible category generalising the category of (subsets of) models of some theory. We prove canonicity theorems for stable, simple, and NSOP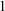 $_1$-like independence relations. The stable and simple cases have been done before in slightly different setups, but we provide them here as well so that we can recover part of the original stability hierarchy. We also provide abstract definitions for each of these independence relations as what we call isi-dividing, isi-forking, and long Kim-dividing.
$_1$-like independence relations. The stable and simple cases have been done before in slightly different setups, but we provide them here as well so that we can recover part of the original stability hierarchy. We also provide abstract definitions for each of these independence relations as what we call isi-dividing, isi-forking, and long Kim-dividing.
Keywords
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



