Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-24T19:16:46.748Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW DP-MINIMAL EXPANSION OF THE INTEGERS

Published online by Cambridge University Press:  04 March 2019

ERAN ALOUF  and
CHRISTIAN D’ELBÉE
ERAN ALOUF
Affiliation:
INSTITUTE OF MATHEMATICS HEBREW UNIVERSITY OF JERUSALEM JERUSALEM91904, ISRAELE-mail: aloufer@gmail.com
CHRISTIAN D’ELBÉE
Affiliation:
INSTITUT CAMILLE JORDAN UNIVERSIT CLAUDE BERNARD LYON 1 69622 VILLEURBANNE, FRANCE and DÉPARTEMENT DE MATHÉMATIQUES ET APPLICATIONS ECOLE NORMALE SUPERIEURE 45 RUE D’ULM, 75005PARIS, FRANCE E-mail: delbee@math.univ-lyon1.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the structure 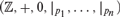$({\Bbb Z}, + ,0,|_{p_1 } , \ldots ,|_{p_n } )$, where 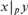$x|_p y$ means 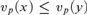$v_p \left( x \right) \leqslant v_p \left( y \right)$ and vp is the p-adic valuation. We prove that this structure has quantifier elimination in a natural expansion of the language of abelian groups, and that it has dp-rank n. In addition, we prove that a first order structure with universe ${\Bbb Z}$ which is an expansion of 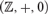$({\Bbb Z}, + ,0)$ and a reduct of 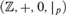$({\Bbb Z}, + ,0,|_p )$ must be interdefinable with one of them. We also give an alternative proof for Conant’s analogous result about 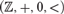$({\Bbb Z}, + ,0, < )$.

Keywords

03C0703C1003C4003C4503C5003C65expansions of the group of integersPresburger arithmeticdp-minimalityintermediate structures
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 2 , June 2019 , pp. 632 - 663
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aschenbrenner, M., Dolich, A., Haskell, D., Macpherson, D., and Starchenko, S., Vapnik–chervonenkis density in some theories without the independence property, II. Notre Dame Journal of Formal Logic, vol. 54 (2013), no. 3–4, pp. 311–363.Google Scholar
Aschenbrenner, M., Dolich, A., Haskell, D., Macpherson, D., and Starchenko, S., Vapnik-Chervonenkis density in some theories without the independence property, I. Transactions of the American Mathematical Society, vol. 368 (2015), no. 8, pp. 5889–5949.Google Scholar
Conant, G., There are no intermediate structures between the group of integers and Presburger arithmetic, this Journal, vol. 83 (2018), pp. 187–207.Google Scholar
Conant, G., Stability and sparsity in sets of natural numbers. Israel Journal of Mathematics, 2019, https://doi.org/10.1007/s11856-019-1835-0.Google Scholar
Conant, G. and Pillay, A., Stable groups and expansions of $({\Bbb Z}, + ,0)$. Fundamenta Mathematicae, vol. 242 (2018), no. 3, pp. 267–279.Google Scholar
Dolich, A. and Goodrick, J., Strong theories of ordered Abelian groups. Fundamenta Mathematicae, vol. 236 (2017), no. 3, pp. 269–296.Google Scholar
Dolich, A., Goodrick, J., and Lippel, D., Dp-minimality: Basic facts and examples. Notre Dame Journal of Formal Logic, vol. 52 (2011), no. 3, pp. 267–288.Google Scholar
Guignot, F., Théorie des modèles du groupe valué $({\Bbb Z}, + ,v_p )$. Séminaires de structures algébriques ordonnées 2012–2013, no. 89.Google Scholar
Kaplan, I. and Shelah, S., Decidability and classification of the theory of integers with primes, this Journal, vol. 82 (2017), no. 3, pp. 1041–1050.Google Scholar
Lambotte, Q. and Point, F., On expansions of (Z,+,0), preprint, 2017, arXiv:1702.04795.Google Scholar
Mariaule, N., The field of p-adic numbers with a predicate for the powers of an integer, unpublished.Google Scholar
Marker, D., Semialgebraic expansions of c. Transactions of the American Mathematical Society, vol. 320 (1990), no. 2, p. 581.Google Scholar
Palacín, D. and Sklinos, R., On superstable expansions of free Abelian groups. Notre Dame Journal of Formal Logic, vol. 59 (2018), no. 2, pp. 157–169.Google Scholar
Pillay, A. and Steinhorn, C., Discrete o-minimal structures. Annals of Pure and Applied Logic, vol. 34 (1987), no. 3, pp. 275–289.Google Scholar
Poizat, B., Supergénérix. Journal of Algebra, vol. 404 (2014), pp. 240–270.Google Scholar
Shelah, S., Classification Theory, North-Holland, Amsterdam, 1990.Google Scholar
Simon, P., A Guide to NIP Theories, Cambridge University Press, Cambridge, 2015.Google Scholar
Wagner, F., Stable Groups, Cambridge University Press, Cambridge, 1997.Google Scholar