Article contents
Distinguishing types of gaps in 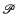 (ω)/fin
(ω)/fin
Published online by Cambridge University Press: 12 March 2014
Abstract
Supplementing the well known results of Kunen we show that Martin's Axiom is not sufficient to decide the existence of (ω1, ϲ)-gaps when (ϲ, ϲ)-gaps exist, that is, it is consistent with ZFC that Martin's Axiom holds and there are (ϲ, ϲ)-gaps but no (ω1, ϲ)-gaps.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2003
References
REFERENCES
- 1
- Cited by


